I believe, that question has been answered above by Sylvain: https://forums.fast.ai/t/lesson-4-official-topic/68643/163?u=gautam_e
Why, in our initialized mnist model, are we checking that it’s greater than 0? Is it because our weights were randomized to mean 0 and thus our “expected value” for each prediction should be 0?
The negative sign is added because, conventionally, people like to minimize a loss function rather than maximizing a probability function.
Minimizing the negative log loss is the same as maximizing the probability of a target label.
For example, let’s say we are trying to predict a label 1.
Here are the transformations performed from the neural network output activations.
- neural network output activations -> number range: negative infinity to infinity
- softmax(activations) or sigmoid(activations) -> number range: 0 to 1
In step 2, we want to maximize the softmax or sigmoid (maximize activations) to get closer to target label 1 - log(softmax(activations)) or log (sigmoid(activations))
-> number range: negative infinity to 0 because log(0) = negative infinity, and log(1) = 0
To get closer to our target label 1, we want to maximize the log(softmax(activation)), the number gets closer to 0. This means we are maximizing the probability of predicting a 1 (red in the picture).
Assume log(activations) = ln(activations) in the picture
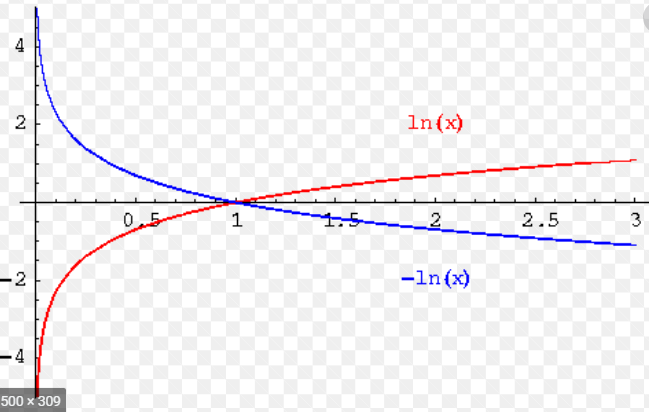
Now, conventionally, people are used to minimizing losses. So, they add a negative sign in front of the log, and now minimize the -log(softmax(activation)). The negative sign flips the log graph vertically.
If you look at the picture, you can see that maximizing log(softmax(activation) (red getting closer to y=0) is the same as minimizing NEGATIVE log(softmax(activation) (blue line). Both are trying to reach the x=1, y=0 point.
Another way to think of it, instead of maximizing negative numbers (log(softmax(activation))). We minimize positive numbers (NEGATIVE log(softmax(activation))).
Paperspace seems to have lost my projects and all of the course chapters and lessons. All that’s remains is a trash folder I created. Has anybody experienced this? Or know how to get the content back?
this is hte second time this has happened to me. The first time was in Week 2, so I just created a new notebook, but now I have saved work I don’t want to lose.
thanks,
JG
@golz You might want to post this in this thread: Platform: Paperspace (Free; Paid options)
Did you save your work in the /storage directory since that is persistent.
Anybody used from_folder() with ImageDataLoaders, dls is empty after this. Any suggestions?
dls= ImageDataLoaders.from_folder(path, train = 'train', valid = 'valid') ??
Thanks
Hi there, we’ve identified a bug in regards to your workspace on which engineers are currently working to amend. In in the interim it is highly recommended to utilize your persistent storage.
That said, rest assured your files are not lost and will appear upon the start of a new instance as I’ve personally taken steps to look into this. I will stop your notebook now, just give me a few minutes and then once you launch the next one you will have all of your workspace files from the previous iteration.
Lastly, please do not hesitate to open a support ticket with us directly should you encounter any issues so that we may quicker assist you.
@init_27 thanks for the heads up! :]
Did anyone answer the below question from further research?
Create your own implementation of
Learnerfrom scratch, based on the training loop shown in this chapter.
I am sharing based on what I understood. Please let me know if the below implementation is correct. Please ignore the indentations
class MNISTLearner(Learner):
def __init__(self):
super().__init__()
@classmethod
def train_epoch(model, lr, params):
for xb,yb in dl:
calc_grad(xb, yb, model)
for p in params:
p.data -= p.grad*lr
p.grad.zero_()
@classmethod
def calc_grad(xb, yb, model):
preds = model(xb)
loss = mnist_loss(preds, yb)
loss.backward()
Seems good to me in a general sense. I would personally would do it without inheriting from learner though. Looks great for where we are at in the course! I would try plugging it into a notebook and making sure it works there.
Tom, thanks for your help to address this. At the moment, my files are still missing. I’m glad you say they’re not lost, but might you know when this issue/bug might be resolved? There hasn’t been any movement on the support ticket in last 24 hours. Shall I open another one? thanks.
Hi. We just pushed a fix for this issue this morning. And I’ve gone ahead and made sure your next run pulls down all of your notebook files as well. Please feel free to contact me directly should you require any further assistance.
Files restored! Thanks Tom and team!
Thank you for such a detailed reply!
I simply wanted to mention that I enjoy the changes for this “season” of Fastai. I have been following the course since the year Fastai started using Pytorch. There has always been so much to learn, but as a course I think it is much better now.
The first year, using Fastai in depth was… a bit cryptic, to be honest. In this regard, last year’s part 2 (“building Fastai from scratch”) was amazing. I like how this year seems to combine the initial approach of Fastai with this. We now have great results right from the start (classic image classifier lesson), even taken a step forward with deploying options, but then you take time to explain the details of a training loop and how they translate to the Fastai vocabulary.
So great job everyone, and thanks for the effort: it shows.
I believe this is the implementation of the ReLu activation function.
I assume, you’re talking about the line corrects = (preds>0.0).float() == train_y.
Yes, I think the answer is something like how you’ve guessed.
With the initially random parameters of the linear1 model, one would expect either output of the binary classifier to be equally likely. If you checked against a positive or negative number instead, one output would be more likely than the other at the start which wouldn’t make sense. Therefore 0 makes the most sense to compare with. That’s more or less how I would explain it to myself, I guess.
I doubt that this has anything to do with the ReLu activation function, since this is the linear1 model which is xb@weights + bias. At this point of the notebook we still haven’t introduced any activation function. But I’m no expert 
Tom, the course work is missing again today. Thankfully I saved my project in the storage folder so I have access to that. But all the lessons and book chapters are now missing again as of this morning. My Jupyter notebook is “nix4urqz”
Hi Jason. That is surprising. I’ve recovered your files for you so that you may continue working. In the meanwhile the team and I will debug this specific case further and update you with our progress. Again, please don’t hesitate to reach out should you need further assistance in the meantime.
Yes, it’s all back. thank you.
The threshold value and the initialization have (almost) nothing to do
with one another (see clarification below).
You can choose any threshold value thresh (0.0 as in the notebook,
but you can pick -1. or 200.):
-
predgreater thanthreshclassifies the sample as a3; -
predless than or equal tothreshclassifies the sample as a7.
(or maybe it is the other way around).
Now about initialization.
The data is normalized (with zero mean) and the parameters at
initialization also have zero mean. Because of its architecture, the
output of the model will initially have zero mean as well, with maybe half
>0.0 and half <=0.0.
If thresh is set to 0.0, then the model will adjust its parameters
so that (hopefully) most of the time it will ouput a value > 0.0 for
a 3 and <=0.0 for a 7.
If you pick thresh far away from 0.0, then (heuristically
speaking), the model will first need to “drag” the values of its
parameters so that its output has mean equal to thresh, and then it
will adjust its parameters so that (hopefully) most of the time it
will ouput a value > thresh for a 3 and <= thresh for a 7.
But the end result will be the same. (Again, this is heuristics, there aren’t necessarily two very distinct phases, but hopefully it clarifies ideas.)
In short: you can pick any thresh you want, but it is more efficient
to pick 0.0, for training purposes.