This is a wiki post - feel free to edit to add links from the lesson or other useful info.
Lesson resources
Links from the lesson
Elucidating the Design Space of Diffusion-Based Generative Models, Karras et al
I think `c_skip’ is the ‘Expected Value’ of ‘sig_data’
small speako at the beginning. Introduced as ‘here we are in lesson 21’ instead of 22.
Just saw last great lesson and I’m very intrigued by Jeremy’s model to predict noise level (I’m kind of curious about this topica and I’ve experimented a bit with that on my Real Images Island notebook).
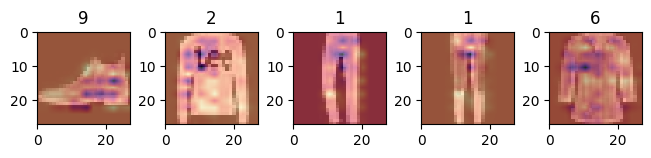
Watching the lesson I’ve realised that fashion minst can be a “biased” dataset for this task because all the images has a white background, and predicting noise level on white background seems to me an easier task.
So to test if this intuition has some foundation, I’ve plotted the grad-cam map to understand if the model give too much attention to the background or not.
Original samples (I’ve focus my attention on [1,9,11,15].
This is the grad-cam with the original image on the background
This instead is the grad-cam map only
Looking at the grag-cam map only for the second and the third items it actually seems that the model is focusing o the background.
Here is the complete “snippet” for gradcam on miniai.
#|export
class Hook():
def __init__(self, m, f, is_forward=True):
register_fn = m.register_forward_hook if is_forward else m.register_full_backward_hook
self.hook = register_fn(partial(f, self))
def remove(self): self.hook.remove()
def __del__(self): self.remove()
class Hooks(list):
def __init__(self, ms, f, is_forward=True): super().__init__([Hook(m, f, is_forward) for m in ms])
def __enter__(self, *args): return self
def __exit__ (self, *args): self.remove()
def __del__(self): self.remove()
def __delitem__(self, i):
self[i].remove()
super().__delitem__(i)
def remove(self):
for h in self: h.remove()
# Just get activations
def save_activations_out(hook, mod, inp, outp): hook.activations_out = to_cpu(outp)
def predict_with_gradcam(learn,xb,yb,show_result=False,display_image=True,ctxs=None):
with Hooks([learn.model[0]],save_activations_out,is_forward=False) as hooksg:
with Hooks([learn.model[0]],save_activations_out,is_forward=True) as hooks:
output = learn.model.eval()(xb.cuda())
act = hooks[0].activations_out
# Get the gradients for the cat class for the first image in the test set
loss = learn.loss_func(output,yb.cuda())
loss.backward()
grads = hooksg[0].activations_out
w = grads[0].mean(dim=[1], keepdim=True)
cam_maps = (w * act).sum(dim=[1])
if show_result:
axs = ctxs if ctxs is not None else [plt.gca()] # Single one if no axes passed
imgs = xb[:,0] if xb.shape[1]==1 else x # Support only BW and RGB
for ax,y,img,cam_map in zip(axs,yb,imgs,cam_maps):
if display_image: ax.imshow(img,cmap='gray')
ax.imshow(cam_map.detach().cpu(), alpha=0.6, extent=(0,img.shape[-1]-1,img.shape[-2]-1,0), interpolation='bilinear', cmap='magma');
ax.set_title(y.sigmoid().item()) # sigmoid has been added only to compare results
#ax.set_title(y.item()) # USE THIS LINE IN GENERAL
return output,cam_maps
samples_to_test = [1,9,11,15]
fig,axs = plt.subplots(1,len(samples_to_test),figsize=(20,5))
_,cam_maps=predict_with_gradcam(learn,xt[samples_to_test],amt[samples_to_test],show_result=True,ctxs=axs);
fig,axs = plt.subplots(1,len(samples_to_test),figsize=(20,5))
_,cam_maps=predict_with_gradcam(learn,xt[samples_to_test],amt[samples_to_test],show_result=True,ctxs=axs,display_image=False);
Note: gradcam output seems fine (the code is supposed to be on 10_activations notebook).
15 Likes
Excellent analysis @ste!
I’ve re-done the t-prediction model using Tiny Imagenet instead of fashion mnist, and still get similarly-accurate predictions. So whilst you’re right that it was able to “cheat” a bit, it turns out it still does a good job without cheating 
10 Likes
Thanks for another great video. Its good to see how things are evolving and I appreciate the approach that is being taken.
On a slightly off topic note - do you have any idea when the course will be released to the public, some colleagues of mine have followed the initial lectures that were released and are keen to follow up with the later ones.
I would like to say how much I appreciate this course, and how grateful I am for the time and commitment of all of the authors.
1 Like
In the next couple of weeks hopefully.
2 Likes
Will Lesson 23 be live today? 07/Feb
2 Likes
No we haven’t recorded it yet.
1 Like
WARNING: this grad-cam code has some issues if used with rgb images due to:
- a typo:
imgs = xb[:,0] if xb.shape[1]==1 else xs - the fact that if the image “i” is a colored image
xb[i]=(c,w,h)its channel dimension “c” should be transposed before to be displayed with mtplotlib:img=img.permute([1,2,0]) - given that we’re feedint it to the model, xb is supposed to be “normalized” at this stage (in this case with mnist
mean,std), so before displaying it we need to denormalize it:img=std*img+mean - last but not least, it would be better to always freeze weights with
learn.model.eval=Truebefore this : you can’t dowith torch.no_grad...because grad-cam is based on gradients
Suddenly (as in the last couple of days) importing UNet2DModel from diffusers gives error!! Used to work just two days back. Any one else see this problem or have a workaround?
from diffusers import UNet2DModel gives the following error:
NameError: name ‘PreTrainedTokenizer’ is not defined
The above exception was the direct cause of the following exception:
…
raise RuntimeError(
687 f"Failed to import {self.name}.{module_name} because of the following error (look up to see its"
688 f" traceback):\n{e}"
RuntimeError: Failed to import diffusers.models.unet_2d because of the following error (look up to see its traceback):
name ‘PreTrainedTokenizer’ is not defined
The issue at this link NameError: name 'PreTrainedTokenizer' is not defined - TextualInversionLoaderMixin · Issue #2906 · huggingface/diffusers · GitHub seems related but I am not sure.
Suggestions, Workarounds appreciated and thanks in advance.
I’d like to ask a question about the no-t technique to check if I understand things correctly. Does it double the amount of compute required?
i.e. one run through a model to predict t value and one run through another similarly sized model to denoise?
For some reason my model wouldn’t train with ddpm_init and would lead to NaN loss after about 5 epochs. Removing the init allowed it to train fine for later epochs but the loss never gets as low as the correctly initialized version.
I had a different outcome when I tried to sample without passing timestep to the model and not using any abar predicting model.
Firstly, I made a change in t range that we pass into the function to get alpha_bar.
Ideally our alpha_bar’s range is between (0.0063, 0.999) from DDPM paper. I used inv_abar function to get specific t range where alpha_bar values does not fall out of the range and used this t range while sampling.
This has made things much better. I got an FID of 5.9 with just 50 steps.
Here is my sampling code:
def inv_abar(abar): return (2/math.pi)*(abar.sqrt()).acos()
# Derived for abar fn - use this range instead of 0, 0.999
trange = (torch.tensor(0.0064), torch.tensor(0.9494))
class DDIM_SchedulerV3: # This is only for sampling purposes - All bugs fixed!
def __init__(self, abar_fn = abar_fn): fc.store_attr()
def set_timesteps(self, ts):
self.num_timesteps = ts
self.timesteps = reversed(torch.linspace(trange[0], trange[1], ts))
def _get_variance(self, alpha_bar, alpha_bar_prev, beta_bar, beta_bar_prev):
return (beta_bar_prev / beta_bar) * (1 - alpha_bar / alpha_bar_prev)
def _get_prev_ts(self, ts):
skips = 1000/self.num_timesteps
each_step = 1/1000
return ts - skips*each_step
def _get_alpha(self, ts):
return self.abar_fn(ts) if ts >= 0 else torch.tensor(1.)
def step(self, xt, np, ts, eta = 0.8):
ts_prev = self._get_prev_ts(ts)
alpha_bar, alpha_bar_prev = self._get_alpha(ts), self._get_alpha(ts_prev)
beta_bar, beta_bar_prev = (1. - alpha_bar), (1. - alpha_bar_prev)
x0_hat = (xt - beta_bar.sqrt() * np)/(alpha_bar.sqrt()).clip(-1., 1.)
var = self._get_variance(alpha_bar, alpha_bar_prev, beta_bar, beta_bar_prev)
sigma = (var*eta).sqrt()
xt_new = alpha_bar_prev.sqrt() * x0_hat + (beta_bar_prev - sigma**2).sqrt() * np + torch.randn(xt.shape).to(xt.device)*sigma
return xt_new
def ddim_sample_v4(model, n_steps, out_shape = (256, 1, 32, 32), sched = DDIM_SchedulerV3()):
sched.set_timesteps(n_steps)
xt = torch.randn(out_shape).to(model.device)
for ts in tqdm(sched.timesteps):
with torch.no_grad(): np = model((xt, torch.tensor([0.]*out_shape[0]).to(model.device)))
xt = sched.step(xt, np, ts, eta = 0.8)
return xt
Here are the results:
I’m not understanding the point of the no-t model. Since you have t known in each step, why would you not want to pass it to your model? Surely having it run a prediction model step on all the images is slower?
What’s the benefit?
I believe the point of having the t-model is to make sure the diffusion model removes the correct amount of noise and the model will hopefully have a better starting point for the next iteration of noise removal.
Imagine that you start with pure noise and you want to remove 1.0% of the noise during sampling, but your model removed 0.8% sometimes. If you leave it up to passing in t, you’d have t moving forward under the assumption that 1.0% of the noise was removed when you likely got less in this example. Whereas if you predict t using the t-model, the t-model would likely recognize that 0.8% was removed and it can pass that to your diffusion model to realize that there is still more noise to be removed than expected to ultimately get to 100% noise removed instead of 80% noise removed. (Obviously this is a little exaggerated, but the small changes can add up and being off by a little is noticeable)
Also, I think it was kind of just an experiment to test out to see if having a t-model would make a difference.
