If you’re looking for help with understanding the fundamentals of how deep learning works, such as the basics of SGD and neural networks, post your questions here!
I have a question:
From the Fastbook - intro notebook:
“McCulloch and Pitts realized that a simplified model of a real neuron could be represented using simple addition and thresholding”
From the first lecture: (Edited Recording: 1:17:56)
“Neural networks are basically multiplying things together and adding them up and replacing negatives with zeroes, and you do that a few times.”
The Question is:
Is the “thresholding” from the “simple addition and thresholding” from McCulloch and Pitts’s simplified model of a real neuron the same as the “replacing negatives with zeroes”?
Great question!
It depends to what level of precision and abstraction you mean. So, given this is a beginner forum, I’ll keep it tight.
First off, there’s a bit of “natural language” human shorthand in the description you cite here – which is entirely why the math is important, as machines allow for no such ambiguity. So the answer you’re looking for has two pieces: arithmetic and logic.
At the arithmetic level, the multiplication / addition representations – and the difference in nature that you note in your question – stem from the basic properties / laws of arithmetic because, with the exception of some special considerations in linear algebra and beyond, multiplication is just repeated addition. That’s it.
It’s not quite true to say “all mathematics boils down to arithmetic operations”; many a category theorist would take exception to that. But, being focused on the practical here, we care about how a computer is going to operate on these concepts. So, down in the circuitry of every computer, these foundational arithmetic rules govern even the most complex and abstract of computations. There’s no real difference in an additive or multiplicative “representation”, arithmetically speaking.
The second part is to do with the nature of logic itself. The basic perceptron / “neuronal” model is a bit like a switch. Either it’s triggered “on” (1), in which information flows out. Or it’s “off” (0), in which case, no information flows.
You will see this concept play out in the concept of activation functions (which are dealt with later in the course). The clearest example of how your question plays out in practice is the activation function known as “ReLU” (the rectified linear unit). The following graph will help:
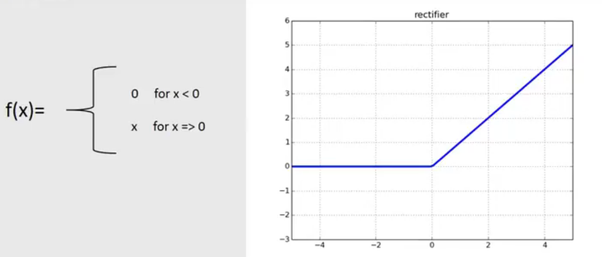
This very much illustrates the concept…below a certain threshold (0 in this case), a neuron will not “fire a signal”. “Information” will not be passed from one neuron to the next unless we have crossed the threshold. Below the threshold, the magnitude of the number is irrelevant; the signal will not be passed along.
So, yes, as you write, “the “thresholding” from the “simple addition and thresholding ” from McCulloch and Pitts’s simplified model of a real neuron” is "the same as the “replacing negatives with zeroes”
Hope this helps!
That’s a great observation ![]() Just for the sake of curiosity, are you a mathematician?
Just for the sake of curiosity, are you a mathematician?
Very much no! Though I love mathematics and mathematical thinking, I’m not “professionally” trained as such.
Just to build upon the fine answer above…: the Rectified Linear Unit that Nick cited is a specific case of thresholding.
Some things are worth noting about ReLU:
-
It is nonlinear, that is, is different from a simple line (or a plane). Nonlinear activation functions are among the main reasons for which neural networks are so powerful and can practically approximate any function.
-
This nonlinearity is achieved in a very simple way, that is: if you give that function some value, it leaves such value untouched if greater than zero, or set it to zero if was originally smaller than zero.
-
No matter being so simple, researchers started to use the ReLU function with neural networks only just a decade ago, while the McCulloch-Pitts artificial neuron was conceived in 1943. One of the main reasons for this was that we are trained to avoid functions that have non-differentiability points, that is points where the fuction itself sharply changes its slope.
All these aspects cause quite deep and important consequences. You will learn extensively about them. Stay curious ![]()
Thanks @balnazzar; these are great additions!
The history of our field and some of the basic intuitions behind it really are quite extraordinary. And, as you allude to, the mysteries and beauties (really, very profound beauties) are a real joy and challenge as the journey progresses.
Thank you Nick so much… you have provided a great explanation, it is 100% clear to me.
So this thresholding is what contributes to the property of “Universal Approximation” - that says simple neural nets can approximate continous functions.
For example take a simple dataset exhibiting a sine wave:
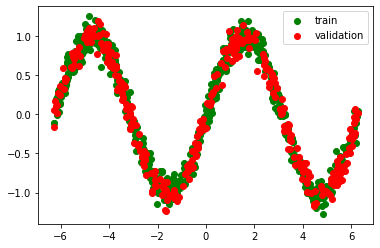
A simple (2 hidden layer) neural network without thresholding cannot approximate this function:
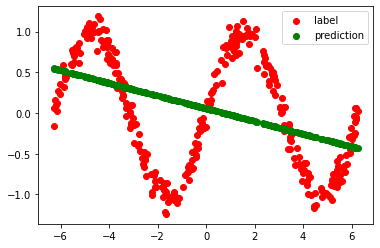
However, if we introduce the thresholding (ReLU) between the 2 layers, the same network can magically learn to predict (approximately) as per the sine wave function:
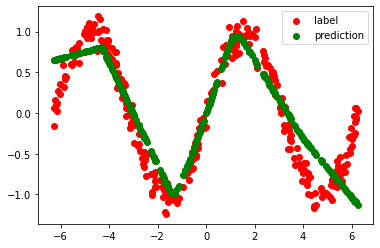
P.S: The code uses concepts which you will learning in upcoming lessons, but if you are adventurous you can check it out.
In my understanding, this is implying that he’s talking about a ReLU type of an activation function which essentially is “replacing negatives with zeroes”.
Also there’s a lot to unpack in that one sentence. “Multiplying things together” refers to w1 * x1 … wn * xn operation (multiply each input with its respective weight) and adding refers to where we simulate the “integrative behavior” of a so called biological neuron. We just add all these inputs which have now been modified to reflect the strength of each incoming connection (via the multiplication by weight operation) and that is what the activation function gets as its input.
A biological neuron doesn’t control the strength of each incoming dendrite (at the tactical level) so it is only concerned with whatever signal is being pumped in via any given synapse, and then a spike occurs when the sum total of all inputs makes the internal potential go over “a threshold” (not sure what it is tbh… maybe like -70 microvolts or something like that?)
But in our ANNs we calculate the strength of each connection by multiplying each input with its strength (or weight) and THEN add them up (which is the key part actually). In biological neurons the strength of each neuron is in the synapse or number of synapses and how much signal each “pre synaptic neuron” sends forward to us. In an artificial neuron (or node) need to encapsulate that synaptic process in the “multiplication” piece to account for the “strength” of each incoming input, and the back propagation basically adjusts these strengths.
All the various ‘activation’ functions in these artificially simulated nodes try to capture that process (in my limited understanding)
That’s right - but don’t worry about the details; we’ll get to them very soon.
From the first lecture:
Neural Networks is a mathematical function that takes inputs and multiplies them together by one set of weights and adds them up and dose that again for a second set of weights and then take all the negative numbers and replaces them with zeros, and then take those as inputs to the second layer and do the same thing multiply them and adds them up and dose that a few times.
The Questions are:
1- Is the number of sets of weights must be (or are) an exact match to the number of batches from the input dataset?
2- if the answer to question 1 is “No”, is the number of sets of weights a variable that the model designer can self-set as see fit?
3- why Jeremy says sets of weights?, did he means that the weights go to the model in batches like the input dataset?
@falmerbid, Its 30 years since my brief undergrad encounter with neural nets, so this may be wrong (and when I’m corrected I’ll have learnt something) - but I understood this to mean…
“Each set of weights is a layer in the neural net.”
thank you bencoman for your answer…
your answer sounds correct but it doesn’t match Jeremy illustration that I have provided in my question above.
as per my understanding from Jeremy, for each layer we multiply and sum up inputs by multiple sets of weights then we take the result from all of that multiplication and summation as input for the next layer.
I think you and me would like another opinion or more clarity on my question.
We’ll be covering that in detail in a future lesson. For now, the key takeaway is that the basic foundations of a neural net are very simple!
I’ve noticed that whenever you train for a single epoch, several things happen underneath the cell.
- Training runs for a single epoch to fit / connect the head of the pre-trained model to our new random head for the purposes of whatever we’re doing
- Then it trains again for a single epoch (as specified), updating as per our training data.
But for each epoch, it seems like there are two separate stages. One is slow (what I think of in my head as the ‘real training’) where the progress bar completes one cycle of 0-100% and then it again goes through the progress bar from 0-100% quite a bit faster.
What are those two separate processes going on underneath? (Possible we might find out about those at a later stage, in which case feel free to tell me just to wait until a later lesson  ) Should I think of them as two separate processes? Is it some kind of consolidation or calculation that’s being represented there?
) Should I think of them as two separate processes? Is it some kind of consolidation or calculation that’s being represented there?
I think the first slow step is the ‘real training’ of updating the parameters on the training data, and the second fast step is calculating the metrics on the validation set (with the now updated weights).
Off the top of my head, I believe you’re talking about the different progress bars of training phase followed by a validation phase (on the separately held out validation data).
Jeremy will definitely get into more details about these in the upcoming lectures.
I wondered about that too. I sort of figured the general idea as you describe but would be good to know about the two stages during the second epoch , maybe there’s a way to make the output more verbose (or maybe not.)
EDIT: I’m not sure if I’m looking in the right place but looks like the progress callbacks has some details on what might be happening behind the scenes:
From the docstring:
_docs = dict(before_fit="Setup the master bar over the epochs",
before_epoch="Update the master bar",
before_train="Launch a progress bar over the training dataloader",
before_validate="Launch a progress bar over the validation dataloader",
after_train="Close the progress bar over the training dataloader",
after_validate="Close the progress bar over the validation dataloader",
after_batch="Update the current progress bar",
after_fit="Close the master bar")
I’m not sure if there is a way to make the progress bars “announce” what they’re doing so to speak , ie print out which call back is being called etc.
Why do we choose error rate instead of accuracy when we’re training our model? Is it a tradition or just something that people do? Accuracy seems more intuitive to me somehow…