Hi all,
this course has been terrific for me so far since it allows me to understand the inner workings of the fastai’s library and use them for my needs, and in particular, tabular data. In this topic I will present my progress on transforming what we learned to a tabular dataset, namely the dataset from Otto Kaggle competition.
I know about the tabular options fastai provides, but I’d much rather know how to implement stuff on my own. This is for several reasons:
- More often than not, I need some special customization to the data handling. Images data are mostly similar in shape, but tabular data is very heterogeneous, and each dataset requires tweakings of its own.
- I’d really like to be able to try the ideas presented here (initialization, custom layers, etc) on my favorite datasets

- I have several specialized architectures I am developing (mainly related to autoencoders), and I want to benefit from the amazing research tools that were given so far in this course (callbacks, layer statistics, metrics, etc.) while studying them.
- In the spirit of this course, doing it will force me to use the tools and recreate them for my needs, which to my feeling will be the best way to learn.
And why the Otto dataset?
no strong reason here. Its advantages are that its relatively simple (all features are similar in distribution), has moderate amount of samples (not too long to train, but not tiny), is well rated being a Kaggle competition and I have lots of experience with it…
Also, normalization of this dataset is not a trivial issue and I hope the init research on it will provide some new insights.
I’ll use this topic as a kind of a diary for my progress, and I also invite anyone who has similar interests, i.e. trying what we learn on tabular data, to post here as well what she’s doing!
I decided to start from notebook #5, and see how it goes from there. The first thing to do is to load Otto dataset, instead of loading MNIST. I override the get_data() function with my own version (after downloading the dataset from Kaggle):
def get_data(valid_pct=0.2):
import pandas as pd
df = pd.read_csv('../../../data/otto/train.csv')
target_name = 'target'
df[target_name] = df[target_name].astype('category').cat.codes # replace string labels with ints.
df = df.drop('id',1)
valid_mask = np.random.rand(len(df)) < valid_pct
x_train = df.iloc[~valid_mask].drop(target_name,1).values.astype(np.float32)
y_train = df.iloc[~valid_mask][target_name].values.astype(np.long)
x_valid = df.iloc[valid_mask].drop(target_name,1).values.astype(np.float32)
y_valid = df.iloc[valid_mask][target_name].values.astype(np.long)
return x_train, y_train, x_valid, y_valid
Now I try to continue with the rest of the notebook. We defined in NB#4 the get_model function which returns a pytorch sequential object:
nn.Sequential(nn.Linear(m,nh), nn.ReLU(), nn.Linear(nh,data.c))
Lets look at the model by typing learn.model:
(0): Linear(in_features=93, out_features=50, bias=True)
(1): ReLU()
(2): Linear(in_features=50, out_features=9, bias=True)
)
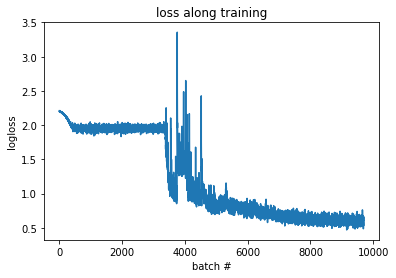
which looks fine for a starting model. Fitting for 20 epochs (LR=0.01) gives:
train: [0.50778127929156, tensor(0.7997)]
valid: [0.5754367667622667, tensor(0.7828)]
It’s not amazing but also not bad. The Kaggle winners got logloss ~ 0.38 and accuracy of above 83% so we still have room for improvement (which is good for our research!). After doing that I noticed I forgot to normalize the data! I do it with:
train_mean,train_std = x_train.mean(),x_train.std()
x_train = normalize(x_train, train_mean, train_std)
x_valid = normalize(x_valid, train_mean, train_std)
and now the results of the same fit are:
train: [0.5099700296131825, tensor(0.8005)]
valid: [0.5568894527170857, tensor(0.7817)]
which is slightly better.
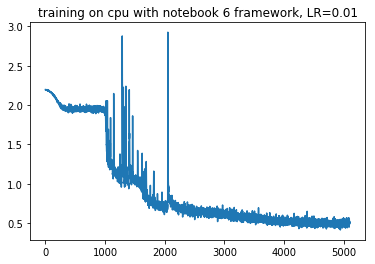
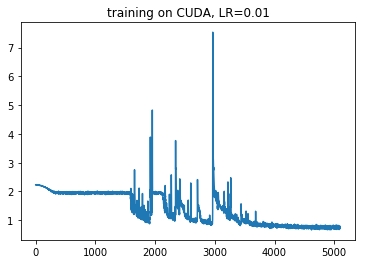
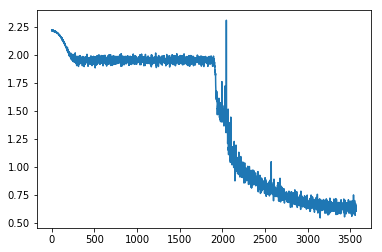
LR Scheduler:
I created the following scheduler
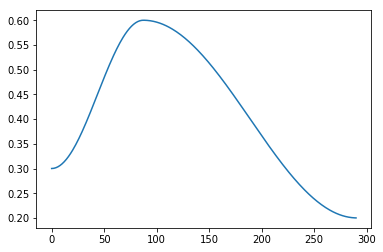
and fitting with that gives
train: [0.5130191078997147, tensor(0.8015)]
valid: [0.5479801731690297, tensor(0.7850)]
Which starts learning slower, as expected, and maybe improves the log-loss in a tiny bit more.
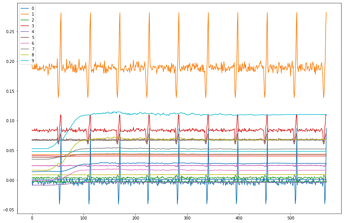
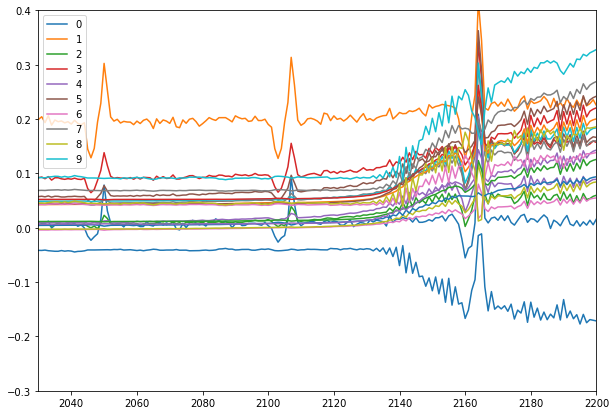
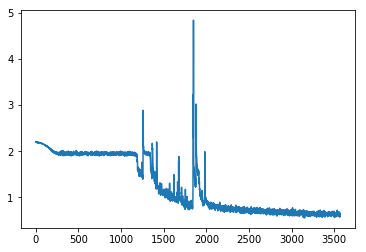
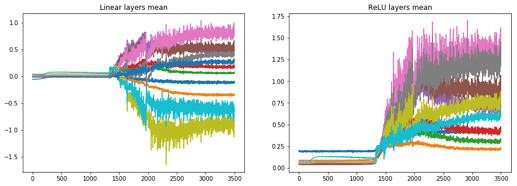
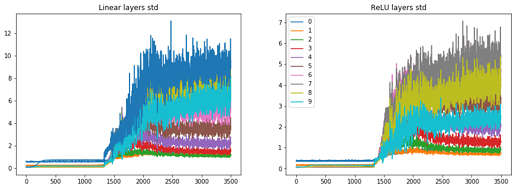
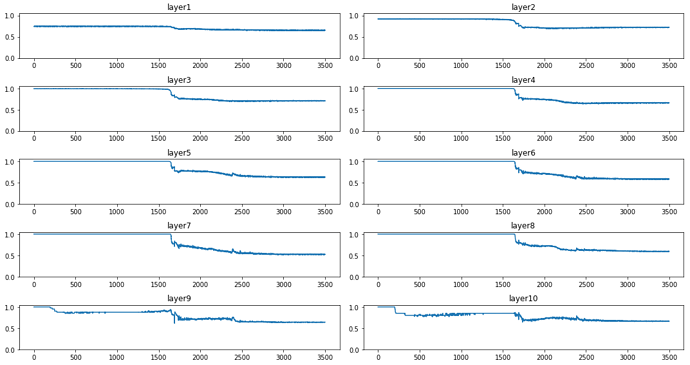
What else can we do? How about initialization?
Embarrassingly, I’m actually not sure what is the initialization I’m using here.
We define the model layers using pytorch linear layer module. We do not provide any arguments there, so the parameters are probably initialized with default. checking the pytorch source for the Linear class, I find it is initialized with:
init.kaiming_uniform_(self.weight, a=math.sqrt(5)) which has the dreaded sqrt(5) Jeremy was referring to, but as we saw in lesson 9, in the uniform case it is actually correct to have it, or is it? in pytorch docs it says that a is the slope of the leaky relu, but we use normal ReLU, so shouldn’t a be 0? how can we try it now to see what is better?
I think i’ll stop here, because this post is starting to be gigantic. I’ll continue in a new post under this topic.
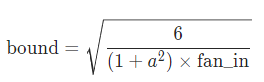
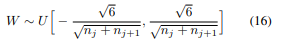
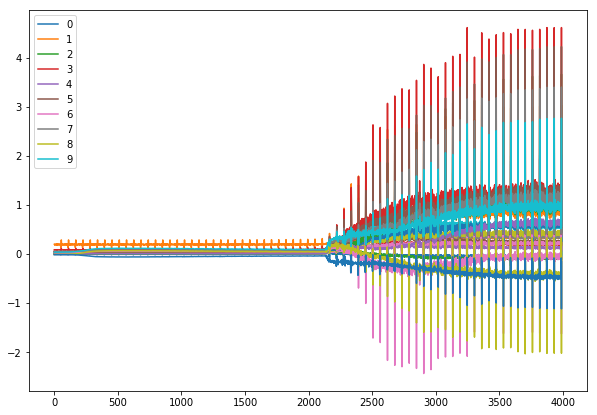

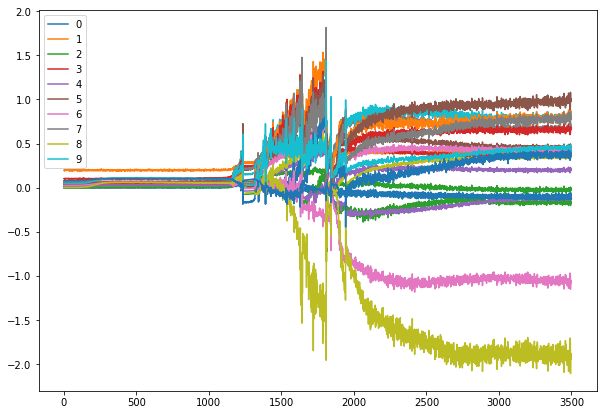
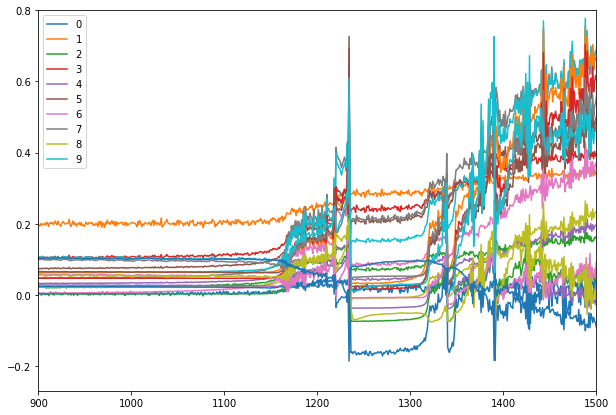
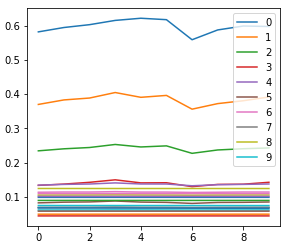
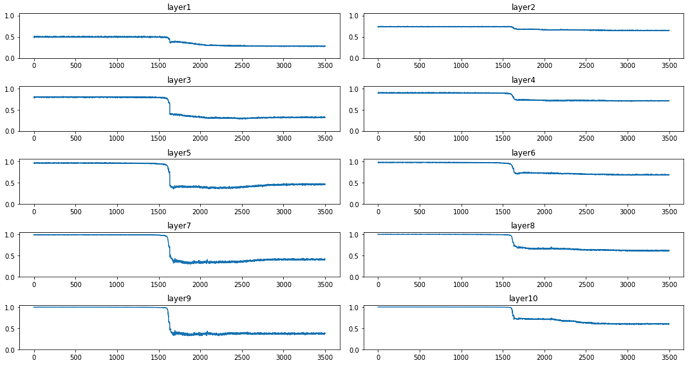
 for each number?
for each number?