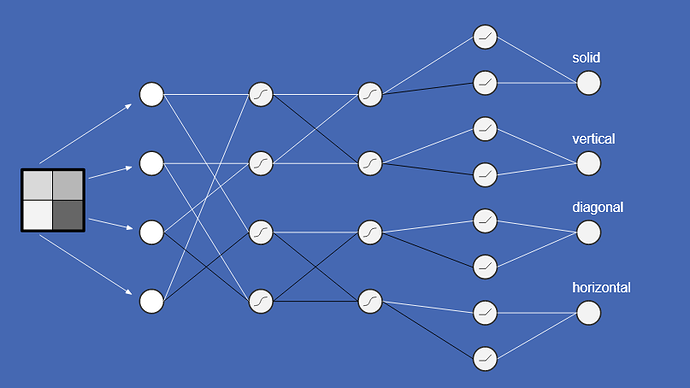
Hello,
I am trying to train a network for this problem (recognizing line types in a 2x2 pixel image):
The input is a 4 pixel image where each pixel can be either black (-1) or white (1). The output also has 4 neurons, each representing one of four categories (solid, vertical line, diagonal line, horizontal line).
I programmed my own simple feed forward neural network and implemented backpropagation as the training method. There is only support for fully connected/dense layers without bias nodes.
As activation functions there are sigmoid/logistic, tanh, ReLU and identity/linear (for output layers).
I used a learning rate of 0.01 and the following network topology (like the picture above):
5 layers (input layer with 4 neurons, 4 neuron dense layer (tanh), 4 neuron dense layer (tanh), 8 neuron dense layer (ReLU), 4 neuron output layer (identity/linear).
When I set the weights explicitly as given in the pictures (black=-1, white =1, the missing ones = 0), the predictions work perfectly as expected.
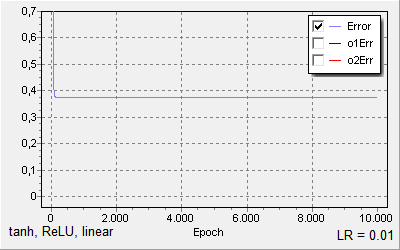
When I try to train the weights with backpropagation however the error/loss never goes significantly lower than 0.4, which results in misclassification of even the training examples.
Same, but with learning rate of 0.1:
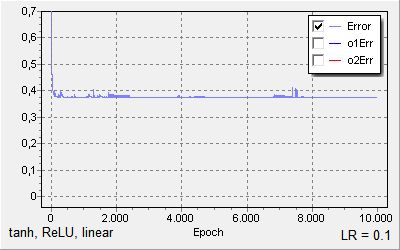
When I ramp up the learning rate to higher than 0.1 I get floating point overflows.
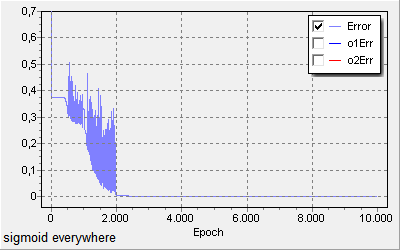
Replacing all the activation function with sigmoid/logistic function and using a learning rate of 10 works however, even if the resulting loss graph is really unsteady, the final result has a very low loss and perfect accuracy.
Using tanh for the first two layers, then ReLU and finally sigmoid, with a learning rate of 0.1, results in this loss graph:
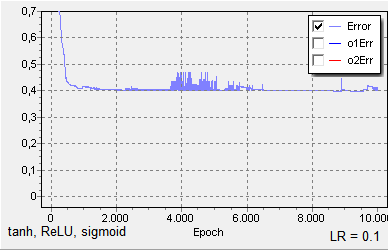
Finally, I noticed that when I use a linear activation in the output layer, training progresses slowly (or not at all after the fast drop, depending on the initial random weights):
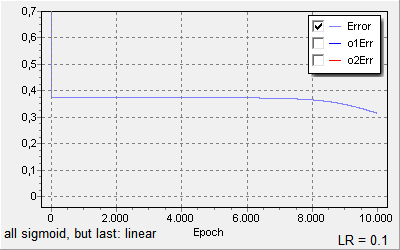
A learning rate of 1 does not bring any improvement. A learning rate of 10 produces floating point overflows.
I thought of vanishing gradients, but the network is really shallow and it still does not explain the huge variations in the “sigmoid everywhere” graph.
What are possible approaches to improve learning with the architecture using ReLU and TanH?
What are possible mistakes I made?
P.S.: For anybody curious, the video from which this screenshot is taken is available here:
https://www.youtube.com/watch?v=ILsA4nyG7I0