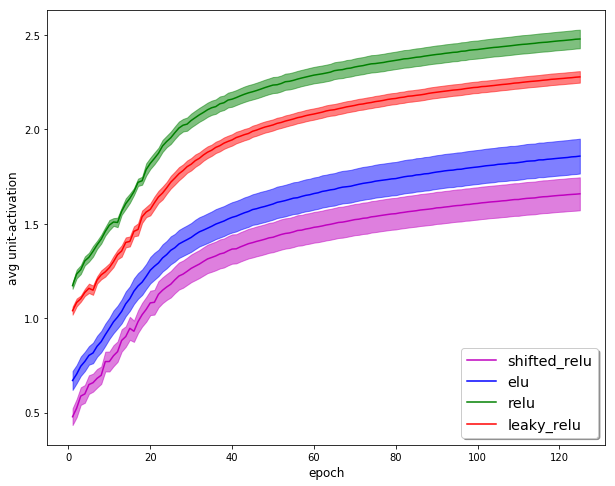
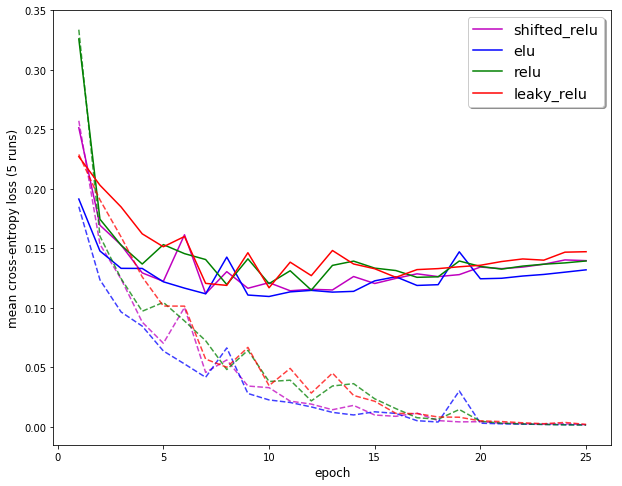
As Jeremy suggested in last night’s lecture, I tried subclassing nn.ReLU and added a constant -0.5 shift to it. I plugged it into a modified single-channel, shrunken-down ResNet I’ve been using for my Magic Sudoku app (the input is basically identical in format to MNIST).
class shiftedReLU(nn.ReLU):
def forward(self, input):
return F.threshold(input, self.threshold, self.value, self.inplace) - 0.5
I pulled the ResNet and BasicBlock classes from torchvision's ResNet implementation and replaced nn.ReLU with shiftedReLU as defined above.
It seems to have dramatically decreased the training loss but didn’t do much for training loss or accuracy. The biggest difference is in the first epoch where the shifted relu did much worse.
Here’s the output of fit_one_cycle from a few weeks ago.
epoch train_loss valid_loss error_rate accuracy
1 0.186894 0.175872 0.058128 0.941872
2 0.086348 0.087768 0.028518 0.971482
3 0.053646 0.106015 0.031677 0.968323
4 0.046601 0.049357 0.017113 0.982887
5 0.037949 0.027546 0.009331 0.990669
6 0.033589 0.018919 0.006171 0.993828
7 0.018287 0.020058 0.006578 0.993422
8 0.013359 0.014329 0.004357 0.995643
9 0.010926 0.015629 0.004546 0.995454
10 0.009849 0.012810 0.003776 0.996224
11 0.003071 0.010585 0.002900 0.997100
12 0.002972 0.011666 0.002914 0.997086
13 0.000561 0.011291 0.002368 0.997632
14 0.000085 0.012187 0.002249 0.997751
15 0.000177 0.012452 0.002235 0.997765
And here’s the output from this afternoon after modifying ReLU:
epoch train_loss valid_loss error_rate accuracy time
0 0.314576 0.243694 0.079613 0.920387 02:53
1 0.080145 0.075431 0.024889 0.975111 02:51
2 0.072920 0.065042 0.020266 0.979734 02:55
3 0.036023 0.034078 0.011040 0.988960 02:55
4 0.032858 0.027199 0.008889 0.991111 02:55
5 0.022661 0.020598 0.006760 0.993240 02:58
6 0.019699 0.021478 0.006164 0.993836 02:56
7 0.014048 0.021239 0.006207 0.993793 02:57
8 0.012207 0.017040 0.005212 0.994788 02:56
9 0.007839 0.012296 0.003622 0.996378 02:57
10 0.004507 . 0.012291 0.003376 0.996624 02:57
11 0.000943 0.011359 0.002802 0.997198 02:58
12 0.000763 0.012123 0.002578 0.997422 02:55
13 0.000805 0.011969 0.002340 0.997660 02:57
14 0.000020 0.011902 0.002277 0.997723 02:59
Unfortunately my initial output was generated with an older version of fastai though so it’s not an exact comparison.
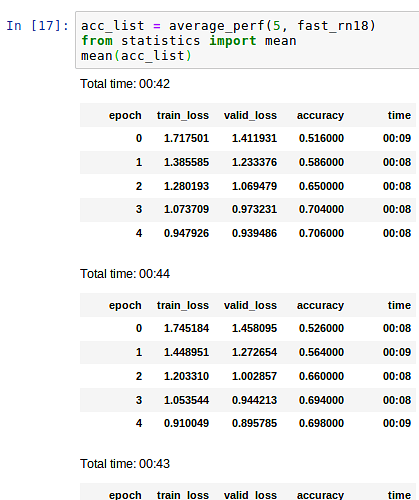
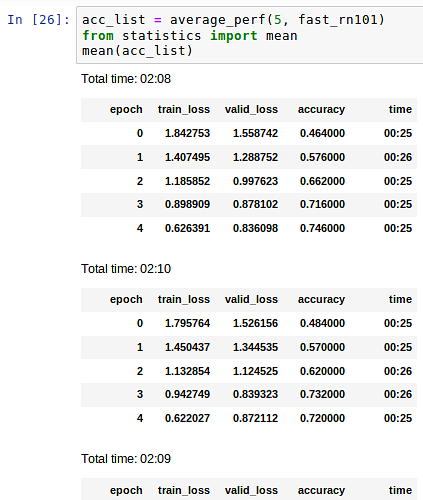
 the “bag of tricks” xresnet18 gets 0.846 average after 5 epochs and xresnet101 gets 0.836. Changing ELU to ReLU in xresnet doesn’t seem to help. I don’t have an intuition for why it’d work so well in resnet but not xresnet though; they are very similar. I’m going to keep poking at it.
the “bag of tricks” xresnet18 gets 0.846 average after 5 epochs and xresnet101 gets 0.836. Changing ELU to ReLU in xresnet doesn’t seem to help. I don’t have an intuition for why it’d work so well in resnet but not xresnet though; they are very similar. I’m going to keep poking at it.