Hello everyone,
I want to share a project I’ve written, in which I develop a data augmentation technique.
The approach, which I call “CDA” (for Combinatorial data augmentation) is designed for classification problems in which the number of labelled images is very low, even for standard transfer learning. For example, 24 labelled images in total for a binary classification problem (it works with even less images).
In the README and jupyter notebook:
I describe the technique in detail, and test it thoroughly on the Fashion MNIST dataset, but I’ll describe it briefly here as well.
Just a note: I have not read about this approach elsewhere, so to the best of my knowledge, this is a novel approach. Please let me know if you’ve seen anything similar somewhere else.
I focus on the binary case, but the same ideas can be applied for multi-class problems.
Suppose we want to classify images from these two categories (these are two classes in Fashion MNIST):
And suppose we have only 12 images from each class, so 24 labelled images in total. We could leave 8 images for validation and use the other 16 for transfer learning on resnet34, tuning the weights of the last layer. That’s going to be the benchmark, but it is unlikely to yield very accurate results on a Test set (disjoint from Train and Valid) due to the low number of examples.
What CDA does is to produce a large set of collages from the 16 images used for training. These collages are simply 3x3 arrays of images taken randomly among the 16 available for training (could be also 2x2, 4x4, etc.).

Because there are 9=3x3 locations, and 16 images available, the number of different collages is 16^9>10^{10}. We would obviously not consider all possible collages, but only a subset large enough. The label of a collage is given by the class that occurs the most among the 9 images in it. The combinatorial nature of the procedure to generate collages gives the name to the technique.
Once the desired number of collages is generated, a transfer learning from resnet34 is applied using them, and because the number of collages is now large, one can tune more than just the last layer of resnet34, which gives a neural network N_{alt}.
Finally, one applies a transfer learning on N_{alt}, based on the 16 original training images, just as it was done for the benchmark, adjusting the weights in the last layer.
The intuition is that because N_{alt} has learned to classify the collages according to the majority class in them, and this has been done for thousands of images (potentially millions), N_{alt} has learned already a lot of useful patterns related to the problem of interest. Therefore, a further transfer learning starting at N_{alt}, and based on the 16 original images, would likely do a better job at classifying the two original classes.
Experiments
Easy pair
For example, working with an easy pair: coat vs boot:
these are some of the collages obtained:

And the following shows the error rates on Test set (1000 images from each class) for both the benchmark and CDA, for different values of m=|X_t|:
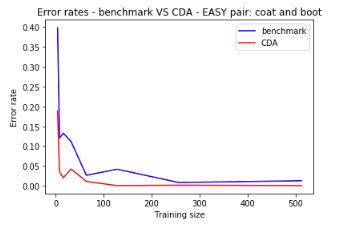
As m increases, both benchmark and CDA decrease their error rates, but CDA is always significantly lower than the benchmark. Here we have the ratio between their error rates (CDA/Benchmark):
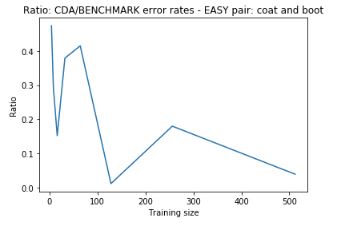
which goes from 0.5 to below 0.1.
Hard pair:
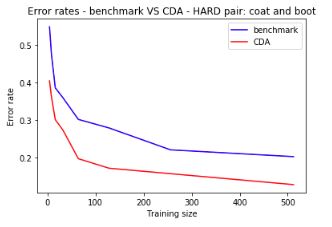
Similarly, for a hard pair: pullover vs shirt:
we get collages such as:

Error rates are still significantly lower for CDA:
More results in the notebook!

