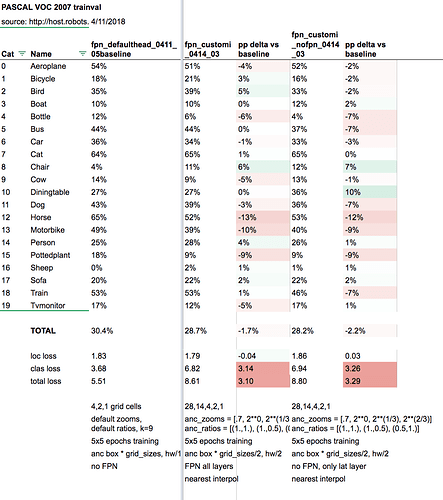
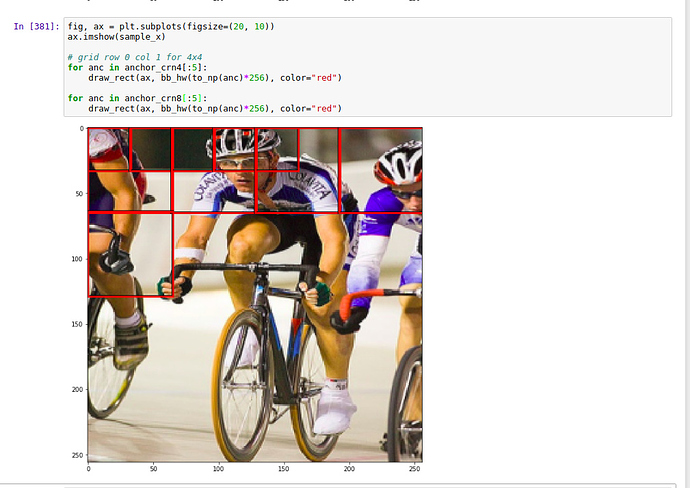
Whoops sorry about the confusion - I didn’t realize either that the manner in which anchors are created changed between our notebook and the official one. Will be more careful going forward to check the diff.
Update: To pinpoint and clarify exactly how we went off-track…
Our version:
anc_x = np.concatenate([np.tile(np.linspace(ao, 1-ao, ag), ag)
for ao,ag in zip(anc_offsets,anc_grids)])
anc_y = np.concatenate([np.repeat(np.linspace(ao, 1-ao, ag), ag)
for ao,ag in zip(anc_offsets,anc_grids)])
for anc_grids=2 and k=1, produces anchor_cnr:
Variable containing:
0.0000 0.0000 0.5000 0.5000
0.5000 0.0000 1.0000 0.5000
0.0000 0.5000 0.5000 1.0000
0.5000 0.5000 1.0000 1.0000
[torch.cuda.FloatTensor of size 4x4 (GPU 0)]
which draws the anchor boxes going top–>down each column (note the number of each box: 0, 1, 2, 3)

Official pascal-multi version:
anc_x = np.concatenate([np.repeat(np.linspace(ao, 1-ao, ag), ag)
for ao,ag in zip(anc_offsets,anc_grids)])
anc_y = np.concatenate([np.tile(np.linspace(ao, 1-ao, ag), ag)
for ao,ag in zip(anc_offsets,anc_grids)])
produces anchor_cnr:
Variable containing:
0.0000 0.0000 0.5000 0.5000
0.0000 0.5000 0.5000 1.0000
0.5000 0.0000 1.0000 0.5000
0.5000 0.5000 1.0000 1.0000
[torch.cuda.FloatTensor of size 4x4 (GPU 0)]
which draws the boxes going left–>right and then next row down:

This is the correct arrangement of boxes that lines up with how the receptive fields are ordered (left–>right and then next row)
The only difference between the two versions is the order in which we use np.repeat and np.tile for anc_x and anc_y. Given [0,1] and repeats=2:
- np.repeat makes [0,0,1,1]
- np.tile makes [0,1,0,1]
So switching the order of the functions as applied to anc_x and anc_y flips the x,y coordinates (0,1) <–> (1,0) and transposes the ordering of the anchor boxes.
Subtle yet important difference! as I’ve unwittingly discovered…


 I don’t think the mAP calculation is wrong because I’ve found that my visual inspection of the predictions vs gt bboxes lines up pretty closely with changes in the mAP and it is calculating as I’d expect in other applications.
I don’t think the mAP calculation is wrong because I’ve found that my visual inspection of the predictions vs gt bboxes lines up pretty closely with changes in the mAP and it is calculating as I’d expect in other applications.