@diganta That’s a very interesting paper indeed. Took the time to read after work. Would be great to find the edge of chaos for Mish. If you have code I can take a look, already using Mish for my work with interesting results, so anything that can help make it better would be good for me. The math behind the papers aint my strong suit, but it serve me well to help.
2 Likes
I have to run but here’s something I want to add into MXResNet that will help us boost things further I think:
Basically, replace the 1-3-1 bottleneck with a series of convs to achieve multi-scale resolution (kind of like Seb self attention to some degree).
Code is on their github but I couldn’t get it working yet…(spent about two hours on it, constant tensor size mismatch).
Anyway, provides about a 2% boost for imagenet (similar complexity as regular resnet bottleneck) and hoping it can do the same for us.
4 Likes
Good find! I’ll try to take a look at it and fumble around later this week.
@Redknight and @Diganta let me know how that goes, I definitely want to learn how to visualize those techniques!
1 Like
@Redknight It is indeed a very interesting paper. The notion of EOC was proposed in this paper here - https://arxiv.org/pdf/1611.01232.pdf and was also explained excellently in this paper - https://arxiv.org/pdf/1711.04735.pdf. Their findings if replicated for Mish might just confirm the mathematical superiority of Mish over other activation functions. However, I’m facing some issues building up the algorithm they used to generate those plots. I have no doubts in the mathematical aspect of it however need help in the coding part.
1 Like
You can find their ICML slides here: https://icml.cc/media/Slides/icml/2019/104(12-11-00)-12-11-35-4383-on_the_impact.pdf
1 Like
@diganta LOL you just pushed click a few seconds before I was going to send the link. From what I could gather the plot is actually the array of outputs of a random initialization under those conditions when feeding a constant (I am ‘guessing’ that part based on similar stuff that I have done that looks like that) and then graph them as a 2d function.
@Redknight The issue is the integral term in the fixed point dynamic q* equation which generates the phase plane boundary separating the Ordered and Chaotic Phase. For Mish, this integral doesn’t hold valid. I tried obtaining the integral from Mathematica and it said “No integral found within scope”. I’m not sure if I’m doing it correctly or not. I have emailed the authors. Hopefully, they reply.
I just tried for Swish and Wolfram gives me the same result. I guess I’m doing something incorrect.
Just wanting to be sure I am understanding this correctly. Boundaries are the hyperparameters we initialize our activation function with, and Ordered vs Chaotic is whenever we have vanishing and exploding gradients?
And if so, so we are looking for somewhere right in the middle correct?
Partially correct. Boundary (defined as q*) is the set of standard deviation values for the weight and bias matrix initializer for which the given activation function won’t result in exploding or vanishing gradients. And it is not a compulsion that the phase plane boundary will be in the middle. For example, this is for Tanh:
2 Likes
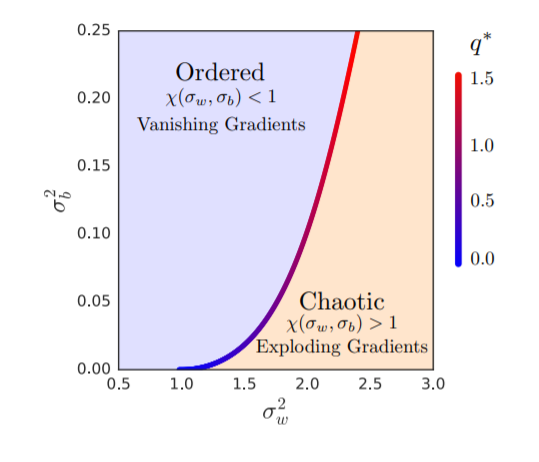
Ah thank you! That helped clarify things quite a bit 
So for the example image you posted, it would be at a bias of roughly >0.05 but <0.1? (if I am reading this correctly)
So it’s more like any pair of weight and bias Initializers standard deviation on that line will do.
1 Like
Got it. Thank you very much for the clear explanations @Diganta
1 Like
I’ll replicate the results of this paper today and I also had a talk with the author. Hopefully we can see some progress.
1 Like
Someone mentioned this earlier, about how useful it is to have these discussions here on the forum and I just want to reiterate that fact. It is very nice to have all of us here and having such a healthy environment discussing these complex ideas and yet bring it down in a way for the rest of the forum to understand (and myself a lot), and also make it comfortable enough to where no question feels stupid. Having this has definitely boosted my confidence in doing this type of work and discussing it. Thanks guys 
9 Likes
I’m also enjoying watching you folks developing deep expertise and turning it into great results! 
5 Likes
@Diganta I would have called that a math problem 
… we can always approximate, we only need a number from a practitioners point of view (of course). BTW those 2 papers reminded me of: https://weightagnostic.github.io/ (paper: https://arxiv.org/abs/1906.04358 ). It has a WTF moment at the end, its one of those papers you will enjoy reading, if you havent already.
2 Likes
I am dedicated to solve it and obtain the EOC and ROC for Mish. But I had heard of this paper. Hadn’t read it though. I’ll surely read this. There’s just so much progress made in this domain in every passing day, sometimes it gets overwhelming. Haha. Again, that’s because maybe I’m still an undergraduate and unfazed of the whole research scenario and pace that I need to get acquainted to.
1 Like
@Diganta Don’t worry you’re not alone in this endeavor! I am as well
1 Like
@LessW2020 there is a couple of comments (except mine) on your Meet Mish article on Medium which I think you should address.