Investigation Question
What happens to a 2-neuron model when you give it a ReLU?
Investigation part 1
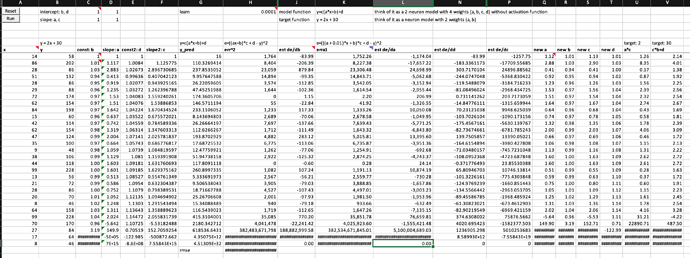
What happens when you train a 2-neuron model with 4 weights to find a simple linear function y = 2x + 30?
Summary
- The model can’t finish training the first epoch
- The error value is exploding near the end of the epoch
- So do the values of all weight and their derivatives with respect to error
Experimental data
Investigation Part 2
Why do errors, weights and derivatives all go exploding? Given SGD using derivatives to tell the model which direction should weights go and by how much, why would weights and errors go crazy?
yes, derivatives of weight to error do tell us which direction to go in order to decrease error, and also tell us if the weight goes up by 0.01 how much lower would error go. However, neither you nor the derivative tell you how far your weight is from the optimal value for error to be minimum.
So, when you calculate how big a step your weight is taking, SGD says besides using derivatives and you should put a knob (i.e., learning rate) to adjust the weight step manually, which is very clever.
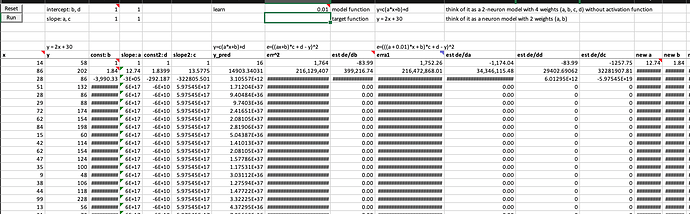
Your model won’t train without an appropriate learning rate
Setting an appropriate learning rate is very important to ensure we can start training without exploding, because you could image the first step of your weight can be so large that your weight can’t move closer to the optimal value and error can’t go down. See what happens to the model when setting learning rate from 0.0001 to 0.01 below
Experimental data
So, having an appropriate learning rate at least for the starting section of the dataset is crucial to keep training going, meaning weights can move in good steps toward optimal weight values and error is decreasing.
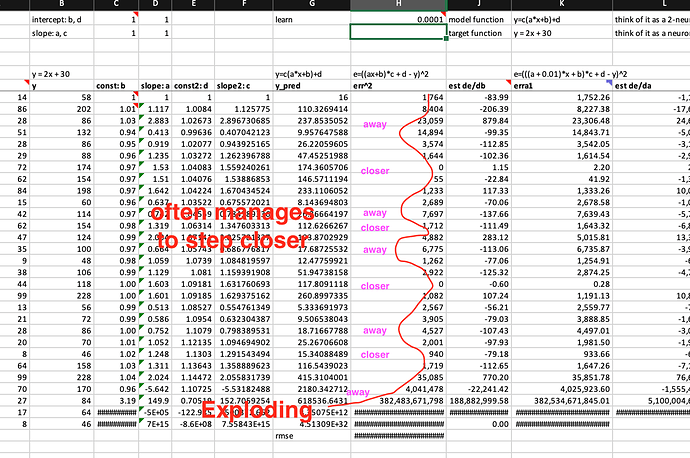
Derivatives of changing weights seem unpredictable, how SGD using learning rate to manage weights toward optimal in most cases?
However, one shoe size can’t fit all feet. You can’t guarantee the next derivative value is always smaller than the previous one. In fact, sometimes, the derivatives can go much larger than the previous derivatives. As long as the derivatives are not too large, and the step size is still appropriate, given the correct moving direction provided by derivatives, so the weights can still move towards the optimal regardless how fast or slow.
How derivatives and errors go exploding under SGD’s reign?
However, in some cases the derivatives can be so large that the learning rate is no longer appropriate, and the step the weight makes is a big step away from the optimal even though the direction provided by the derivative is correct. And the derivative at the new point may well even be larger, and therefore the weight will even further away. It could become a self-reinforcing loop to move further and further away from the optimal. No chance to bring them down anymore. So, derivatives and error all go exploding. (see the graph above)
This is today’s investigation and speculation. If you find anything suspicious or wrong, please share with me, thanks ![]()