Lesson 9 official topic

[drscotthawley (Scott H Hawley)]

In Lesson 9A “Stable Diffusion Deep Dive” by @johnowhitaker, at the point where we visualize the 4 channels of the latent representation of the parrot image,…

# Let's visualize the four channels of this latent representation:

Since those representations are inside a VAE, does that mean that two of those channels correspond to mean values (of normal distributions), and two of the channels correspond to standard deviation (or variance)?

…and if so, which channels correspond to which statistical properties?

[johnowhitaker (Jonathan Whitaker)]

The latents used are a sample from the VAE’s predicted distribution (or the mean of the distribution depending on which code you use, the variance is typically so tiny the two are almost equivalent in this particular model)

[johnowhitaker (Jonathan Whitaker)]

The output of the VAE is a latent distribution, and in the deep dive notebook I do latent_dist.sample() to draw a sample from this distribution and return it as the latents.

[drscotthawley (Scott H Hawley)]

Ah, ok! I see now that we can go “inside” the latent.latent_dist to get .mean, .std, and .var values. If we plot those values (scaled by that factor of 0.18215) we see that the means are (visually) indistinguishable from the sampled values, because – as you said – the variance is so tiny:

Thank you!

---

Although… this leaves me wondering: why are we using a VAE at all then, if the variances are microscopic? Doesn’t that destroy the nice latent-space-regularization properties (and generative properties) that you’d get from a VAE? i.e., why not just use a regular autoencoder?

[drscotthawley (Scott H Hawley)]

Dear Mac users: I modified the “Stable Diffusion Deep Dive” notebook so it will also run on Mac / Apple Silicon / MPS.

I sent in a Pull Request to the main repo, but in the meantime you can find my version here.

[UmerAdil (Umer H. Adil)]

I had the same issue even after updating all libraries (!pip install -Uqq transformers diffusers fastcore).

My mistake was that I forgot to include .to('cuda') at the end of this line: StableDiffusionPipeline.from_pretrained('CompVis/stable-diffusion-v1-4', revision='fp16', torch_dtype=torch.float16).to('cuda').

Now it runs perfectly.

[santy (Santy Gegenschatz)]

Hi guys!

I am working on understanding and testing myself on lesson 9.

This might be a silly question, but here goes. At one point we say we:

want embeddings from the text and image encoder to be similar

Then, we conclude we can use dot product to measure this similarity (whether they go in the same direction)

However, my doubt is why don’t we use euclidean distance. Intuitively, it sounds that if the distance is 0 then the embeddings would not only be close but actually the same ones, which i guess is kind of what we want.

Anyway, if somebody want to correct / help me steer my thoughts that would be great!

Thanks in advance

[Kamui]

We can indeed use euclidean distance or dot product or cosine Measuring Similarity from Embeddings  |  Machine Learning  |  Google for Developers

[bencoman]

@kamui Nice link. Nearby I found a nice diagram clarifying what an AutoEncoder is, which would have made it seem less like magic when I first encountered it (I’m a visual learner). Examples of “Predictor” are the well known Cat/Dog and Bird/Forest NNs.

[drscotthawley (Scott H Hawley)]

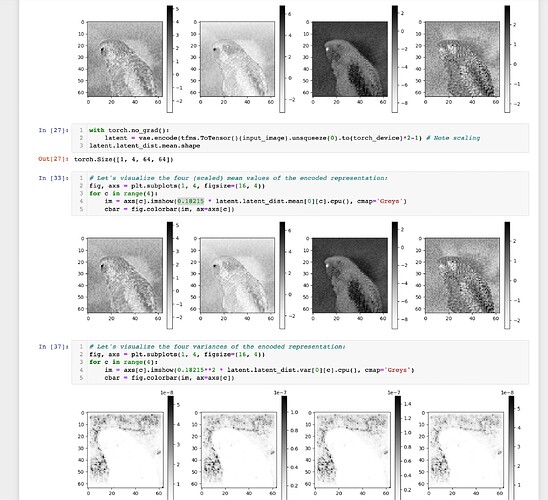
I love your question and I’m going to start with,

TL/DR:
“Sorry, I don’t know exactly why dot product was chosen in this case, but I’m going to make an educated guess that it’s probably because (being the fastest, computationally) it was the first thing they tried, and it worked well enough, and probably changing it out for another measure didn’t (or wouldn’t) make much of a difference.”

Longer answer:
Over the years, I’ve seen a number of hand-wavy general arguments across the web for why one might prefer a particular similarity measure for high-dimensional embeddings, and I have generally found the arguments to be unsatisfying, save for this: dot product is objectively the fastest to compute, and is often “good enough”. In this way, I see a “similarity” with respect to the choice of ReLU activation function over other functions, in that it’s also the fastest to compute and is often “good enough”.

Long ago, Qian et al (2004) found that switching between euclidean distance and cosine similarity didn’t make much of a difference for their retrieval tasks.

The answer in each situation depends a bit on whether the embedding vectors are, say, td-idf scaled for frequency, and whether or not you “care” about the effects thereof. This little quiz from Google highlights how different choices for similarity measures might affect one’s results.

…One may also note that the Transformer models use a dot product similarity where they normalize by the total number of dimensions of the space…which may be another influence on the choice of dot product as a sufficient measure of similarity in this case.

In the CLIP model, it’s been noted that the choice of cosine similarity over dot product was to limit the dynamic range in order to help stabilize training – see Why cosine loss instead of just dot product? · Issue #68 · openai/CLIP · GitHub – but presumably the SD folks found other ways to “stable”-lize things.

I wish it were feasible for individuals to easily train one’s own Stable Diffusion + T5 model from scratch and swap out the similarity measures to see what difference it makes. Maybe in 10 years some new computing advancement(s) will make that possible.

PS- I look forward to later readers correcting me or filling in the gaps here!
PPS- As an aside: if anyone knows “why” the value of the the cosine similarity of softmax-normalized vectors asymptotes to \tanh(1) as the number of dimensions increases, I’d be very curious to learn.

[jeremy (Jeremy Howard)]

Just one thing to note on this:

(a-b)^2 = (a-b)(a-b) = a^2 + b^2 - 2ab

As you see above, the euclidian distance (a-b)^2 expands out to contain the dot product ab. The other components are just the scale of a and b. So euclidian distance and dot product are measuring largely the same thing, except that euclidian distance also measures the scale of the data.

(I’m being a bit hand-wavy about not actually dealing with the fact the terms are vectors, but AFAICT it still works out the same either way.)

[galice (Alice)]

Hi,

First, thank you for this very clear course, it makes it easy to learn about stable diffusion.

There is one area however which has confused me slightly: the scheduler.

During training, the role of the scheduler seems clear: it’s here to generate varying degrees of noise and create the data needed to train the UNet. (please correct me if I am wrong here!)

However, I am not sure I understand its role at inference time.
In the code, there is this line
latents = scheduler.step(pred, t, latents).prev_sample.
which comes after
with torch.no_grad(): pred = unet(input, t, encoder_hidden_states=text_embeddings).sample
pred_uncond, pred_text = pred.chunk(2)
pred = pred_uncond + guidance_scale * (pred_text - pred_uncond)
where we are predicting the denoised latent.
I am wondering why we are not simply passing pred_uncond and pred as latents for the next step. Does this mean we are re-adding noise at each step with the scheduler?

[NavneetSajwan]

As I began studying Stable diffusion, it came to me Why can’t we train a classifier and then during the denoising step, instead of predicting the noise,

1. Just make a forward pass on a noisy image
2. Get the loss on it.
3. Use this loss to calculate gradients for the input image.
4. Update the pixel values by subtracting lr * gradient
5. Then pass the updated image to the model and repeat unless we get a good result

[Elfeky (Mohamed Ali Elfeky)]

I didn’t get how the “T” (time steps) relates to the amount of noise if it is just the number of times we will predict the noise for the same image and we set it by ourselves.

second, why do we multiply by “C” (learning rate) if it will result in noise, How could the model know that wasn’t my noise and this a strange noise? I was thinking we would give it any noise and it would give us an image using the guidance of the embedded text.

Thanks

[cygnus]

Hi guys, i was try to follow along the colab notebook on Textual Inversion to train new tokens and i was getting this error when i run this code block in Training function section

import accelerate
accelerate.notebook_launcher(training_function, args=(text_encoder, vae, unet))

for param in itertools.chain(unet.parameters(), text_encoder.parameters()):
  if param.grad is not None:
    del param.grad  # free some memory
  torch.cuda.empty_cache()

and the error is below. Please help me to resolve this issue.

[ZachariasDr (Zacharias Drimiskianakis)]

Hello everyone,

At the 1:54:13 timestep of lesson 9, we can’t see the similarity of two vectors by just multiply them element wise and then sum up (wikipedia’s coordinate definition of dot product), can we?

We have to do the cosine similarity (wikipedia’s geometric definition of dot product). Am i correct?

Thanks in advance!!

Dot product - Wikipedia.

[redghostsilver]

Hi all, when I run the Python Notebook for this lesson, on the very first cell, I get “No module named ‘diffusers’”.

All I did was import the notebook in Kaggle and run the cell.
Am I missing something?

[strickvl (Alex Strick van Linschoten)]

a pip install diffusers should fix that…

[chongdashu (CU Lim)]

Can someone clarify something for me, if the following is correct? This is regarding 9A’s deep dive into stable diffusion.

Token embeddings will differ based on input, but position embeddings are always the same, given that the model always constrains it to max_length=77 ?

This is made apparent with the code below:

prompt = 'A picture of a puppy'

# Tokenize
text_input = tokenizer(prompt, padding="max_length", max_length=tokenizer.model_max_length, truncation=True, return_tensors="pt")
input_ids = text_input.input_ids.to(torch_device)

# Get token embeddings
token_embeddings = token_emb_layer(input_ids)

# The new embedding. In this case just the input embedding of token 2368...
replacement_token_embedding = text_encoder.get_input_embeddings()(torch.tensor(2368, device=torch_device))

# Insert this into the token embeddings (
token_embeddings[0, torch.where(input_ids[0]==6829)] = replacement_token_embedding.to(torch_device)

# Combine with pos embs
input_embeddings = token_embeddings + position_embeddings

#  Feed through to get final output embs
modified_output_embeddings = get_output_embeds(input_embeddings)

print(modified_output_embeddings.shape)
modified_output_embeddings

Note that position_embeddings was simply initialised based on the model, not the input.

[squid (Suchit G)]

Hey there! Really excited to start part 2 of the course!

I went through the lesson 9 video, but couldn’t find some of the content Jeremy was referring to in the video. The notebook for the lesson seems to be truncated.

Update: Only github seems to truncate the notebook. Running it locally or on colab or viewing it on https://nbviewer.org shows that it is just fine!