It needs to be equal to 1 because this derivation should work for arbitrary number of layers. The only way for the product to not go to zero or explode to infinity is to be 1. Since L can be 100 or even 1000 in theory, if it is anything but one, it either collapses to a very small number or explodes to infinity.
Another nice way to get some intuition about what @maxim.pechyonkin is saying is to look at the ‘All you need is a good init’ paper https://arxiv.org/abs/1511.06422 which takes an empirical approach to initialization. Instead of deriving formulas for the initializations of the weights in terms of the parameters of the network architecture, the authors just determine the appropriate scale for the weights by experiment. They feed a batch of inputs through the network layer by layer and scale the weights of each layer to ensure the output always has variance close to 1. The appeal of this approach is that it means you don’t continually have to think about different rules for initialization as you develop new architectures, you can just set them algorithmically.
I’ve also attempted an implementation of it here: https://forums.fast.ai/t/implementing-the-empirical-initialization-from-all-you-need-is-a-good-init/42284
I don’t think I understand this. Let’s say my initialization scheme is for Var(w_1) = 2*n_1*1.25, Var(w_2) = 2*n_2*0.8 ... Var(w_(t-1)) = 2*n_(t-1)*1.25, Var(w_t) = 2*n_t*0.8
This extends easily to an arbitrary number of layers and it still holds that:
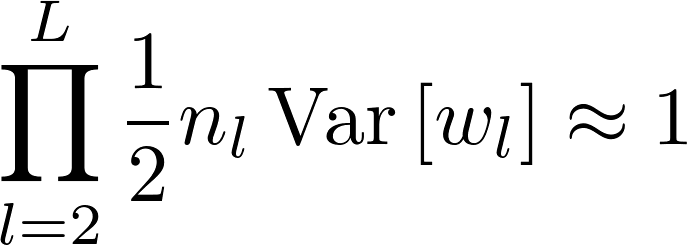
for any L.
I don’t know if this would affect performance but I want to understand if this is still valid.
EDIT: I guess the difference between my reasoning and the authors’ is that the authors try to get every layer’s variance to be close to 1 whereas I am thinking for neither layer to be very far away from 1 (we can deviate a little bit but we have to come back soon to 1 lest the output’s variance be too large or too small)
Yes, this is still valid, at least as far as the argument in the paper is concerned. There are many other valid configurations (alternating between between 0.5 and 2 is another such configuration). That’s why they say in the paper that
A sufficient condition is:
\frac{1}{2}n_lVar[w_l] = 1, \quad \forall l.
(emphasis mine, as opposed to a necessary condition). So the answer to
Did the authors choose to make every multiplication equal 1 because it was easier?
is yes.
Is that so bad, if your standard deviations don’t get out of control later on (and actually end up closer to 1 in the end)? I’m wondering if you just noticed this somehow or if this is actually negatively impacting your training/results.
If you were really dead set on it, you could scale down your embedding by 3, and scale the next layer back up by 3.
The embedding vectors are located in a matrix so you could divide it by 3 ?
Hey, I published my own review on the Kaiming paper, without the derivation but with all the important intuitive concepts. I hope it serves as a complement of @PierreO’s post. You can find it here. Feedback is appreciated!
Hi @Kaspar and @mediocrates
I suspect you are both right. Multiplying the embedding matrix like that should be fine and, on the other hand, I am not sure yet this is having a measurable negative impact as it is. I was wondering about deviations in my model after watching lesson 8, that’s why I looked into it, but it may be fine as it is already (hopefully not: improvements are always welcome!)
I think I will probably try to “normalize” my embedding matrix and see how it goes. It’ll probably be inconclusive, but I’ll let you know if it is an unprecedented breakthrough 
Hi @cqfd, were Statistics 110 lectures enough to understand the maths behind Kaiming He Initialisation paper and also Pierre’s blogpost? At the moment, I am really struggling as I don’t know about Expectation, Variances and Covariances… etc
Yep, Blitzstein definitely covers all those things, and in my opinion in a nice way too 
Awesome, thanks! 
Before diving into many hours of stats lectures I’d suggest checking out Khan Academy on statistics. If you’re starting from “What the hell is covariance?” (like me!) it will get you up to speed very quickly. To be fair, it only covers these concepts in scalar form, not the matrix stats used in the Kaiming paper, but at that point you’ll have the idea and you can decide how much further you want to take it.