So the truncated backprop is truncated every batch size?
It’s a one-layer recurrent model.
1 Like
how many parameters an RNN end up having if we really only have one layer repeated multiple times?
Are we changing the parameters on the same layer at each loop, or creating a layer for each loop?
So does self.h represent the one layer? Or is it self.h_h?
self.h represents the hidden state of the RNN. self.h_h is the one (linear) layer.
1 Like
self.h is the hidden state, it’s not a layer. self.h_h is the layer (h_h stands for hidden to hidden).
2 Likes
You could run learn.summary() to figure this out. https://docs.fast.ai/basic_train.html#model_summary -> check this out too.
Would you determine good values for things like n_hidden and n_layers through a standard hyperparameter grid search?
I also got this
Floating point reference to Rachel’s course on Linear Algebra 
lots of fun too. Would love an updated version of that as well
1 Like
Could we somehow use regularization to try to make the RNN parameters close to the identity matrix? Or would that cause bad results because the hidden layers want to deviate from the identity during training (and thus tend to explode/vanish)?
2 Likes
is there a way to quickly check if the activations are disappearing / exploding ?
1 Like
Floating point is discussed starting around minute 54 of this video from the computational linear algebra course:
13 Likes
Thanks Rachel!!!
Check this out: The colorful dimension
4 Likes
Yes, but that could take quite sometime but if you have the compute go for it. Even Random search. I find Bayesian optimization a bit better. Or you look into this method adaptive resampling and this notebook.
How exploding/vanishing gradients work: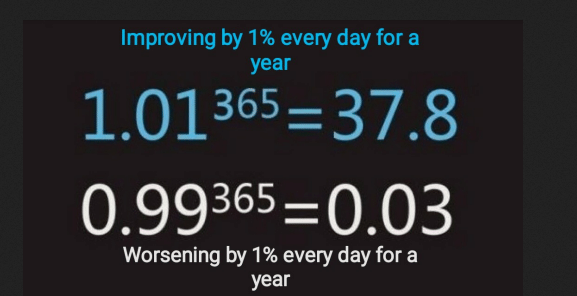 
6 Likes
1 Like
Original dropout paper here
2 Likes
Does dropout somehow skip the computation or just set the activation to zero?