Lesson 5 official topic

David_Gilbertson · September 12, 2022, 9:17pm

I was curious about the requirement of selecting samples “with replacement” in random forests. Obviously if you’re taking N samples (for each tree in the forest) from your training set of size N, then if you don’t use replacement, each tree would get the same data. But what about if you take less than N. It looks like taking about a third is a sweet spot (which is interesting, because it’s also a lot less data!)

When I take only 30%, it appears to not matter whether I use replacement or not (for Titanic, anyway).

In the chart below, each column is a variant of what % of the training data is used for each decision tree (30 dots for re-running the experiment multiple times, the line passes through the mean score). The left hump is “with replacement” the right hump without.

So I guess my question is, what am I missing? Why is a full-sized bootstrap sample (same as the training set) of the data used for each tree when the results appear better when only taking a third. Why is using bootstrap samples the same size as the training data (with replacement) seen as a core part of bagging, when it doesn’t seem to make a difference (unless your bootstrap sample is the same size as the training set).

My guess is that people do do it this way, but it just goes by some other name that I haven’t come across yet.

jeremy · September 12, 2022, 9:33pm

You’re right @David_Gilbertson - using smaller samples is often helpful. And certainly faster! It’s a useful trick I’ve often used in my real-world projects.

jimmiemunyi · September 29, 2022, 1:13pm

Going through this lesson notebook again and noticed this too. I wonder if there was a reason for including the value_counts. For now I am just not including it.

Also, if my intuition is correct, Alone column should be in cat_names not cont_names while creating TabularPandas since it only has 2 levels, True or False.

But we also have to convert it into numerical format first and then the levels will be considered categorical

df['Alone'] = df['Alone'].replace({True: 1, False: 0})

Fares · October 3, 2022, 3:15pm

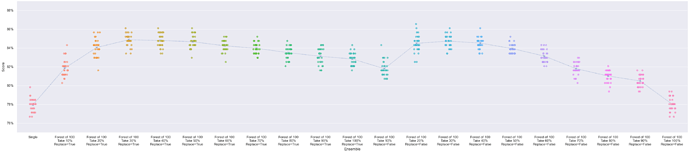
Quick question, I haven’t finished the video yet so maybe my question will be answered later, but when I first read the chapter in the book, we were able to do matrix multiplication using the @ operator.

In Python, matrix multiplication is represented with the @ operator. Let’s try it:

def linear(xb): return xb@weights + bias

When I tried doing the same with the tensor multiplication operation, I had different results:

Using the star (*) operator:
predictors*coeffs

tensor([[-10.1838,   0.1386,   0.0000,  -0.4772,  -0.2632,  -0.0000,   0.0000,   0.0000,   0.2799,  -0.0000,   0.0000,   0.3625],
        [-17.5902,   0.1386,   0.0000,  -0.9681,  -0.0000,  -0.3147,   0.4876,   0.0000,   0.0000,  -0.4392,   0.0000,   0.0000],
        [-12.0354,   0.0000,   0.0000,  -0.4950,  -0.0000,  -0.3147,   0.0000,   0.0000,   0.2799,  -0.0000,   0.0000,   0.3625],
        [-16.2015,   0.1386,   0.0000,  -0.9025,  -0.0000,  -0.3147,   0.4876,   0.0000,   0.0000,  -0.0000,   0.0000,   0.3625],
        [-16.2015,   0.0000,   0.0000,  -0.4982,  -0.2632,  -0.0000,   0.0000,   0.0000,   0.2799,  -0.0000,   0.0000,   0.3625],
        [-11.1096,   0.0000,   0.0000,  -0.5081,  -0.2632,  -0.0000,   0.0000,   0.0000,   0.2799,  -0.0000,   0.2103,   0.0000],
        [-24.9966,   0.0000,   0.0000,  -0.8973,  -0.2632,  -0.0000,   0.4876,   0.0000,   0.0000,  -0.0000,   0.0000,   0.3625],
        ...,
        [-11.5725,   0.0000,   0.0000,  -0.4717,  -0.2632,  -0.0000,   0.0000,   0.0000,   0.2799,  -0.0000,   0.0000,   0.3625],
        [-18.0531,   0.0000,   1.2045,  -0.7701,  -0.0000,  -0.3147,   0.0000,   0.0000,   0.2799,  -0.0000,   0.2103,   0.0000],
        [-12.4983,   0.0000,   0.0000,  -0.5968,  -0.2632,  -0.0000,   0.0000,   0.3136,   0.0000,  -0.0000,   0.0000,   0.3625],
        [ -8.7951,   0.0000,   0.0000,  -0.7766,  -0.0000,  -0.3147,   0.4876,   0.0000,   0.0000,  -0.0000,   0.0000,   0.3625],
        [-11.1096,   0.1386,   0.4818,  -0.7229,  -0.0000,  -0.3147,   0.0000,   0.0000,   0.2799,  -0.0000,   0.0000,   0.3625],
        [-12.0354,   0.0000,   0.0000,  -0.7766,  -0.2632,  -0.0000,   0.4876,   0.0000,   0.0000,  -0.4392,   0.0000,   0.0000],
        [-14.8128,   0.0000,   0.0000,  -0.4905,  -0.2632,  -0.0000,   0.0000,   0.0000,   0.2799,  -0.0000,   0.2103,   0.0000]

Using the at (@) operator:
predictors@coeffs

tensor([-10.1433, -18.6860, -12.2027, -16.4301, -16.3205, -11.3908, -25.3070,  -0.5898, -12.2533,  -7.5595,  -1.7943, -27.0627,  -9.3770,
        -17.1166,  -6.6461, -25.7389,  -0.6738, -11.2936, -14.5495, -12.0601, -16.5340, -15.9226,  -7.2657, -13.1879,  -3.4187, -16.7060,
        -12.0087,  -8.5717, -11.4280, -11.2247, -19.4901, -12.3667, -11.4247, -30.6909, -14.0372, -19.6142, -12.0088,  -9.8399,  -8.3933,
         -7.3825, -18.5810, -12.6974, -12.0264,  -2.0570,  -9.1135, -11.2286, -11.3781, -11.4247, -11.9609,  -8.5294,  -2.9040,  -9.8336,
        -23.7943, -13.6695, -30.9993, -11.3363,  -9.9119, -14.0918,  -2.0923,  -4.4131, -11.0830, -18.0486, -21.1084,  -1.3357, -12.0837,
        -11.7831, -13.6151,  -8.9168,  -7.0005, -11.8921, -14.9523,  -6.7790, -10.2830, -12.9385, -15.3500, -11.6813, -11.2247, -11.2286,
         -0.2588, -14.1475, -10.3254, -13.5767, -11.4257, -13.2503,  -8.0603, -15.1710,  -6.9724, -11.2286, -10.4748, -11.2286, -13.5431,
         -9.3721, -21.5020, -11.7305, -27.4092, -11.2286, -33.8889, -11.5624, -15.8551, -15.9326, -13.1278, -11.2247,  -9.8792, -15.4093,
        -16.9660, -13.0763,  -9.8812, -11.2216, -17.7053, -11.5249, -22.0673,  -7.6666, -10.3028,  -9.3304,  -8.9625,  -9.8368, -32.8981,
        -13.5717, -12.3309,  -0.3477, -10.0058, -11.2286, -16.0716, -15.2797, -25.1549,  -6.4052, -11.3732, -11.2047, -11.9167, -20.9209,
        -16.1925,  -9.3505, -21.9099, -13.6695, -11.7565, -11.6632,  -8.5256, -17.3044,  -7.5528, -12.3160, -11.7323, -10.3467, -11.2821,
         -9.0313,  -8.4906,  -8.8239, -12.6109,  -3.8859, -16.7466, -19.6258, -23.7841, -10.4627, -25.8100, -18.5064, -11.2094, -24.5165,
         -7.7211, -14.0060, -11.2434, -10.1026, -20.3896, -18.7920, -12.1474,  -8.0031,  -0.1266,  -3.9993, -11.2436, -20.1614, -11.2675,
        -13.4984, -28.4508,  -1.5996,  -0.3202,  -9.8368, -26.9188,  -8.0668, -10.8147, -24.1783, -14.0710, -16.2853, -10.1541, -12.1262,
         -3.5373,  -0.3663,  -1.7515, -11.4119, -11.4296, -20.9936, -18.5436, -16.7795, -15.0483,  -8.9791,  -8.8221,  -1.3418, -21.3932,
        -28.2439, -11.3732, -19.3286, -11.4247, -11.3451, -13.1138, -10.1026, -15.8150, -21.9610,  -8.4512,  -0.9088, -14.9338, -13.1330,
         -7.7215, -19.5146, -11.2021, -16.5392, -10.2819, -14.0710, -11.2346, -15.5492, -12.6656, -19.6440, -16.0623, -14.0265,  -7.5254,
        -12.6823, -23.7269, -11.2247, -17.8849, -10.3332,  -8.9346,  -9.5875,  -8.5162, -10.8661, -16.5308, -13.5361, -27.5030,  -1.7372,
        -11.2491, -11.2672, -20.5616,  -3.6075,  -8.9346, -15.4477, -12.0642, -11.4296, -13.5636, -10.2784, -14.7861, -20.6759, -11.7360,
        -10.8863, -17.0612, -25.1906, -11.2077, -13.2685, -28.8629, -14.0113, -18.8602, -14.0468, -12.3674, -14.3629, -17.8792, -23.2881,
        -11.3732,  -0.7599, -24.0973, -17.9291, -11.4247, -16.8039,  -7.0701, -11.5460, -27.2117, -16.7782, -11.3065, -11.1934, -19.0597,
        -17.8756, -11.4247, -29.4768, -20.9934, -10.6968,  -2.9883, -16.1856, -30.3521, -13.0753,  -7.5590,  -8.9141, -11.2681, -16.2112,
        -14.0396, -10.2989, -19.6258, -10.4989, -12.4906,  -9.9456, -17.6480, -11.2992, -11.2247, -12.0837, -11.7773,  -0.9070, -11.3030,
        -24.4177, -11.4247, -11.3266,  -8.4160, -11.4865, -11.2286,  -0.3556, -12.4427,  -9.0598, -14.8652, -15.0713, -12.3783,  -9.1000,
        -12.0399, -13.0763, -19.8598, -12.2009, -11.3550, -25.1962, -14.4886, -19.5130, -10.2819, -12.6134, -14.2639, -10.2121, -10.1026,
        -18.0427, -28.3054, -16.8999, -14.3369,  -8.3538, -11.3781, -21.2405, -17.9022,  -7.4160, -11.5444, -11.2247, -13.6516, -20.3554,
        -20.9495, -21.0572,  -0.8789, -10.9377, -13.1452, -11.7565, -16.8484, -11.3451, -18.7515, -11.2854,  -1.2695, -19.5756, -10.7933,
        -11.3332,  -7.4632, -11.7183, -12.0087, -13.1138, -10.3178, -17.8257, -11.4280, -11.4280, -17.7954, -14.4337, -21.6828, -16.2940,
        -11.3781, -13.9851, -28.8818, -12.0603, -11.4247, -12.3376, -12.5608,  -8.2700,  -8.9141, -11.5107,  -1.1042, -12.2371, -10.3334,
        -13.4432, -10.0451,  -8.9071, -20.9365,  -1.0924, -14.9287, -16.4254, -11.2247,  -8.8943,   0.2159, -16.8999, -11.3727,  -8.8897,
        -16.5417,  -9.8335, -12.7999, -11.8460, -10.9500, -10.2964, -14.5154, -21.6259, -10.7862, -13.1909, -18.1690, -12.1544,  -9.7933,
        -13.0822,  -9.4433, -15.8862, -23.7193,  -1.2710,  -9.8329, -10.8661, -11.2247, -11.3489, -15.7741, -10.6968, -20.4835, -11.2801,
        -15.7919,  -8.0859, -14.0710,  -4.5488, -12.0264,  -9.9841, -13.5387, -12.8724,  -8.2644, -11.2077, -13.2066,  -9.1791, -11.3732,
        -14.9318, -13.1243, -11.2854, -19.6872,  -7.9639, -23.3335,  -6.4094,  -9.4407, -10.4230, -29.1976, -14.4894, -20.8371,  -9.4106,
        -11.5460, -13.1967, -11.2302,  -1.7819,  -6.0985, -15.9017,  -2.9508, -24.2642, -16.3908, -11.2800, -14.8614, -23.7762, -11.2286,
        -14.3409, -30.2516, -11.3329, -23.3360, -11.3732, -22.3823, -15.8576, -22.0008, -22.4032, -11.2286, -17.6827, -10.6968, -26.0855,
        -11.3726,  -0.9835, -11.2077, -17.7240, -15.0535, -11.6963, -10.3950, -11.4206, -15.8862, -13.3779, -10.2892,  -0.9422,  -3.4873,
        -10.6968, -23.2640, -29.3687, -12.6715, -10.8661, -16.5477, -27.8374, -14.0060,  -4.0469, -11.2800,  -9.8190, -25.6529, -33.9677,
         -9.8399, -12.1514, -26.1132, -11.3589, -11.5537, -11.2222,  -8.0031, -10.0360, -11.4215, -17.3333,  -7.8823,  -9.4712, -15.1779,
        -11.2727, -13.2963, -12.5726, -13.6877, -11.2286, -16.8253, -26.0517, -11.2143, -21.9736, -15.9296, -11.6120, -16.9098, -14.9279,
        -14.3803, -10.2989, -12.0087, -21.3150, -12.0088, -19.0111, -23.3360, -11.7454, -18.1690, -10.2870,  -0.9303, -12.0088,  -8.3890,
        -11.8144, -14.0723,  -3.1446, -20.9936, -15.2109, -11.3503, -10.8552, -16.6144,  -3.5880,  -4.5138, -15.0068, -24.2789, -29.7841,
         -9.0405, -12.1088, -15.2112,  -3.7320,  -8.6692, -12.8308, -11.3753, -11.0829, -10.3473, -28.8629, -23.1845, -12.5528, -18.1311,
        -16.8568, -11.3732, -18.6311, -13.1531, -11.2286, -11.2801, -11.1826,  -8.9102, -12.8326, -12.0088, -14.9269, -28.8393, -24.6168,
        -16.8261, -11.4247,  -7.5254,  -9.0358, -15.9741, -18.2931, -12.0643, -14.9287, -11.6083, -19.0068, -25.3291, -17.7197, -12.0463,
         -8.3078, -21.9705, -28.6009, -10.3028, -11.2286, -16.2961, -25.1874, -21.8544, -10.9429, -17.3213, -16.6351, -11.5457, -22.3030,
        -12.0087, -23.6763, -10.9838, -11.2247, -11.3754, -20.4866, -17.1662, -16.7814, -14.0021, -12.6917, -10.8521, -19.1204, -17.1681,
        -11.2021, -11.4296, -11.3732, -16.3205, -11.0754, -15.5984, -12.2112,  -1.8064, -12.1749, -13.4014, -19.6166,  -9.9383,  -9.8350,
         -9.9838, -28.4430, -26.7108, -10.1735, -12.1505, -11.3728, -37.2217, -23.7006, -15.8078, -10.5227,  -3.7016, -13.1967, -14.9287,
        -14.3050, -18.2848, -11.2339,  -9.3721, -12.3376,  -0.4613, -11.6468,  -0.9835, -23.2799,  -8.9102, -26.9507, -11.2158, -10.8043,
        -11.2247,  -8.4487,  -9.8493, -11.4267,  -8.6198, -11.3945, -11.2247, -14.8919, -10.8307, -27.6529, -23.3897, -19.4151, -21.9113,
        -16.7691,  -9.2353, -15.0977, -11.7565, -11.2216, -20.0237, -11.3335, -18.6094, -14.5223, -32.5425, -14.5339, -10.6968,  -8.4442,
        -11.4601,  -8.5435, -18.8681, -18.0497, -11.4345, -13.6976,  -9.4046,  -5.8018, -27.8159, -12.1893,  -6.1443,  -8.9617,  -8.4448,
         -7.3790, -14.5427,  -2.6882, -11.6468, -12.4716, -27.9371, -24.2627, -20.4866, -11.4243, -23.5843, -19.5506,  -9.6883, -16.3624,
         -9.1845, -11.8359, -12.0109, -18.3856, -21.0739, -19.6027, -10.7854, -11.7831, -12.2629, -11.2727, -22.3916, -13.5764, -24.2548,
         -8.9039, -19.0849, -12.6893, -11.5167, -15.3877,  -2.9726,  -7.8234, -15.9226, -23.3290, -12.6754,  -9.3918, -13.8089, -11.4244,
        -11.7665, -11.6013, -14.1005,  -6.1895, -10.6968, -10.8307, -10.8307, -13.4556, -21.8367, -17.8277, -11.2247, -11.2247, -11.2993,
        -16.9295, -10.4887, -11.2339, -14.4658, -32.4038,  -7.3390, -14.1225,  -8.9722, -14.6135,  -1.8295,  -2.7455, -15.4283, -10.7618,
        -22.1850,  -0.1377, -13.0738,  -8.4906, -15.8576, -15.7516, -11.3503, -19.0735, -10.1572, -16.5932,  -7.5184, -23.9220, -12.1620,
        -14.4335, -11.4734, -14.9395, -11.2622, -22.3333, -26.5763, -12.0087, -24.4927,  -8.4436, -11.3732,  -2.5750, -11.3729, -20.3402,
         -6.9684,  -8.1136, -13.6138, -10.8330, -11.6650, -11.6706,  -8.4884,  -3.4512,  -0.1580, -22.4998, -11.3732,  -7.7389, -10.1541,
        -12.1060, -11.6876, -18.2371, -22.8915, -14.5357, -14.7862, -13.9092, -15.9226, -14.3565,  -4.9692,  -0.8856, -12.5887, -14.4619,
        -17.4662,  -8.4957, -18.2371, -15.5043, -12.1503, -18.4033, -16.3410,  -2.1993, -14.2375, -10.5227, -10.8140, -15.1819, -19.9797,
         -4.1131, -24.1846, -12.6321, -17.0033, -12.5179,  -0.5895, -11.3515, -11.6468,  -1.1926, -11.3732, -29.1582,  -7.8981,  -0.2665,
        -12.0088, -10.7608,  -8.4574, -18.9424,  -9.8547, -11.2286, -15.3500, -12.0988,  -9.3739,  -7.5459, -14.9371, -16.8464,  -8.0031,
        -19.5480, -10.1026, -17.1183, -13.1050, -12.2552,  -1.2221, -34.3666,  -4.8911,  -7.4666, -20.6130,  -8.2921, -21.0715, -23.7710,
        -11.5413, -12.0088, -18.9367,  -9.7407, -22.4286, -10.1541, -11.2936, -19.6773, -13.4103, -14.6544, -11.2622,  -1.6574, -12.1505,
        -21.7417, -15.0940, -21.8979, -13.9909,  -7.8940,  -9.4180,  -8.9102, -11.2247, -26.9502, -11.7156, -15.3908, -10.4088, -13.1007,
        -11.6650, -17.4433, -12.6823,  -9.0363, -10.8845, -13.0268, -15.0764])

Why use the star operator and not the at one?
Thanks in advance!

benkarr · October 3, 2022, 4:35pm

I assume you mean t_indep*coeffs (since I can’ find predictors in the notebook). The * here is element wise multiplication. (Using torchs broadcasting) the result of that is: the first column of t_indep gets multiplied with the first element of the coeffs, the second column with the second element and so on, in general:

(t_indep*coeffs)[:,i] == t_indep[:,i] * coeffs[i]

If you have a look at the next code cell (in ‘Linear model and neural net from scratch’)

preds = (t_indep*coeffs).sum(axis=1)

this sums up the result of the element wise multiplication along the rows which is exactly the same as t_index@coeffs by definition of the matrix product.

Maybe it helps to understand the connection if you go through a small example manually, like:

import torch
t_indep = torch.arange(12).reshape(3,4)
coeffs = torch.tensor()

Check what t_indep and coeffs look like, and try to understand how the results of t_indep*coeffs, (t_indep*coeffs).sum(axis=1) and t_indep@coeffs come about.

smail · November 8, 2022, 3:11pm

hey Fastai community;
In 05-linear-model-and-neural-net-from-scratch Jeremy said that we don’t need bias in the process of doing matrix multiplication.
Can someone please explain why we don’t use the constant bias in that specific case?

TonyNguyen · January 8, 2023, 12:06pm

Hi Ismail,

Are you referring to the constant term (i.e the b in mx + b)? To my (very limited) understanding, we used the constant term when Jeremy was going through the excel version of titanic example in Lecture 3, because he used n-1 set of dummy variables for our categorical data (eg. he only had 1 dummy variable for gender), whereas pandas created n set dummy variables for our categorical data. Jeremy said at ~19m:50s of the video that when you use the n-1 level you have to add a constant term (which implies that when you use the n level you don’t need the constant term, which he confirms ~20sec later when he says that he prefers using n because then you don’t need to use the constant term). I hope this was what you were actually after.

Cheers,
Tony

sua · February 15, 2023, 6:53pm

In the “How Random forests work” notebook, what’s the intuition behind using standard deviation? Why is that a good choice of similarity here?

galopy · February 27, 2023, 3:19am

I wrote some blogs about the MNIST project at the end of chapter 4 of the fastbook.

This blog takes the mean of images and achieves accuracy of 66%.
This blog uses neural net and gets 87% accuracy.
This blog uses fastai and gets 99% accuracy.

Hopefully these are useful for those who are working on the project.

lucasvw · February 27, 2023, 8:10am

Standard deviation is a measure for the amount of dispersion in a group of data points. E.g. if all individual data points are very close to it’s mean, that the standard deviation will be low. If all individual data points are very far from the mean, that the standard deviation will be large.

It’s being used in this context because we want to find groups where the dispersion within the group is low → e.g. all data points within the group are very similar to one another. Also, we want the group to not be trivially small (for example just 2 data points) so the group size is multiplied with the std.

Although it’s a nice simple baseline measure, I personally think that this measure is missing something pretty crucial: namely whether the mean of the two groups is different. For example, if we have data that is all centered very closely around a mean, then any split will show 2 groups with small std internally, but if the 2 groups both have the same mean, then it’s still not a strong split.

lucasvw · February 27, 2023, 8:27am

In Lesson 5, in the why-you-should-use-a-framework notebook, FastAI is being used (TabularPandas) to train a network on the Titanic data:

dls = TabularPandas(
    df, splits=splits,
    procs = [Categorify, FillMissing, Normalize],
    cat_names=["Sex","Pclass","Embarked","Deck", "Title"],
    cont_names=['Age', 'SibSp', 'Parch', 'LogFare', 'Alone', 'TicketFreq', 'Family'],
    y_names="Survived", y_block = CategoryBlock(),
).dataloaders(path=".")

learn = tabular_learner(dls, metrics=accuracy, layers=[10,10])

When doing learn.model we can see that a number of Embedding matrices are created:

TabularModel(
  (embeds): ModuleList(
    (0): Embedding(3, 3)
    (1): Embedding(4, 3)
    (2): Embedding(4, 3)
    (3): Embedding(4, 3)
    (4): Embedding(1, 2)
    (5): Embedding(3, 3)
  )
  (emb_drop): Dropout(p=0.0, inplace=False)
  (bn_cont): BatchNorm1d(7, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (layers): Sequential(
    ...

I have 2 questions on this:

Is there a mapping in the learn or dls object which shows which embedding matrix belongs to which variable?
and, which row in any Embedding belongs to which value from its associated variable?

chrwittm · February 28, 2023, 7:40am

Check out the actual code via doc(tabular_learner): Jump to the source from there.
In the code (or the docs) you can find that how the embeddings are created:
emb_szs = get_emb_sz(dls.train_ds, {} if emb_szs is None else emb_szs)
Within get_emb_sz you ca see:

"Get embedding size for each cat_name in `Tabular` or `TabularPandas`, or populate embedding size manually using sz_dict"
    return [_one_emb_sz(to.classes, n, sz_dict) for n in to.cat_names]

The sequence of the embeddings therefore is stored in to.cat_names

lucasvw · February 28, 2023, 8:05am

Thanks for your help @chrwittm! By looking at the source code I found indeed exactly what I’m looking for, all information (order of Embedding matrices and mapping of values to rows) is stored in dls.classes (= to.classes), which gives:

{'Sex': ['#na#', 'female', 'male'],
 'Pclass': ['#na#', 1, 2, 3],
 'Embarked': ['#na#', 'C', 'Q', 'S'],
 'Deck': ['#na#', 'ABC', 'DE', 'FG'],
 'Title': ['#na#'],
 'Age_na': ['#na#', False, True]}

sdCarr · March 12, 2023, 6:36pm

Good afternoon, everyone;
I’m trying to take what I learned in lesson 5 (linear-model-and-neural-net-…) on a dataframe I created with data taken from the Spotify API. In the data preparation phase in one of the columns , the row data obscillate between 0.0 and 0.9 with a shift in the histographic representation to the left of accumulated data, i.e. between 0.1 and 0.2 like this:

My question is whether in this case it would be necessary to fix this as Jeremy explains which is to take the logarithm, which reduces the large numbers and makes the distribution more reasonable ? will it give problems in the model ?
Thanks

prasadkulkarni · March 24, 2023, 6:47am

Hello folks,
am trying to run clean notebook of lecture 5 by myself using kaggle.
trying to train the model but not getting why am i getting the error that “too many values to unpack”

chrome_2uKv2YS9Ju

here’s my kaggle notebook link:

prasadkulkarni · March 24, 2023, 6:53am

Hello @sdCarr
I think applying log is necessary as the data points between 0.0 to 0.2 have greater magnitude and will dominate the results,
Also, in later parts when they are multiplied by coefficients , these values will affect the results by making them biased , Hope this helps!

galopy · March 24, 2023, 5:49pm

Hi,

Can you check what the_coeffs is? I think it should have three tensors in a tuple or a list.
Also, I think there is a problem with initialise function. Why does it reassign n_coeff to another value?

fib1123 · April 16, 2023, 7:03pm

Hi!
I have 2 questions regarding the lesson 5 content.

Can someone give more detailed explanation why when creating dummy variables for all categories we skip bias / constant? We have many other features so why do we skip just because of this specific kinds of features?
When analysing learned weights for different classes we see intuitive relation between sex_male vs sex_female. When one is positive then other is negative. What about the class? Why we see positive weights for all 3 classes? Woudn’t we expect 3rd class to be negative in that case? Or we just analyse relative differences between possible classes? (like class 1 weight > class 2 > class 3) Is it due to colinearity?

Thanks,
Stanislaw

lucasvw · April 17, 2023, 10:12am

Hi @fib1123

Are you familiar with linear regression? It has to do with multi-collinearity and the so-called “dummy variable trap”. Perhaps the easiest way to explain this is with a very simple linear model in which we just regress y on a categorical variable “sex” which can be male or female.

Let’s say we one-hot encode this sex variable so we have:

y = a + b * sex_male + c * sex_female.

Now sex_male and sex_female are mutually exclusive, so either one of them is 1 and the other is 0.

In case “sex_male” = 1, we have practically: y + a + b * 1 + c*0 = a + b
In case “sex_female” = 1, we have practically: y = a + c

Now consider an alternative model:

y = b1 * sex_male + c1*sex_female

So we have
y = b1 for males and y = c1 for females.

So this model is actually fully equivalent to the former but with recoded coefficients: b1 = a+b and c1 = a+c. E.g. we don’t need to include the constant if we use all the categories of our one-hot encoded variable.

Or we just analyse relative differences between possible classes?

Indeed, we would analyse the differences between the coefficients.

fib1123 · April 17, 2023, 10:48am

Great answer Lukas! Thanks
I know linear regression but did not know details about “dummy variable trap”.

I understand the example that you gave in the context of just one variable but it is still less obvious for me why constant would not be useful since we do not have just “sex based feature” but we have many more. So as the rule of thumb: we can skip constant if we encode ALL categorical features with all values?

But we do not have all categorical features, right? Let’s think about having model with just price, then constant / bias term is obviously beneficial:
y = aprice vs y = aprice + b. If we skip bias term we are very limited, don’t we?

So having such feature alone in addition to categorical ones (that I agree allow us skipping) in my opinion justifies usage of bias