This is a wiki post - feel free to edit to add links from the lesson or other useful info.
Thanks for a great lesson, there is a lot to digest in this one, I think it might take me a while but great to see it all coming together
There is one downside to using einops and torch.einsum. They’ve historically had performance issues compared to using the transpose method.
Out of the box using einops with PyTorch 2.0 and torch.compile will also decrease performance, since torch._dynamo doesn’t recognize einops code as traceable. This will cause a break in the model’s compiled graph kicking computation for rearrange back to the slower eager mode. This may be fixed in future PyTorch versions.
There is a workaround using torch._dynamo.allow_in_graph which I have reproduced from chilli in the EleutherAI discord:
from einops import rearrange
from torch._dynamo import allow_in_graph
allow_in_graph(rearrange)
This will tell dynamo that rearrange is traceable, allowing PyTorch to compile rearrange into the model graph. I believe this will work for most, if not all, einops methods.
allow_in_graph is not required for torch.einsum since dynamo is aware of it.
I noticed that we have an imports.py in the miniai folder. Is this manually created or was it autogenerated by nbdev. I am not so familiar with nbdev and in my own version of the repro have been avoiding manually changing things in this folder.
I manually created imports.py
FYI, there was an error in this video (h/t @ste for spotting) where I accidentally drew the heads in multi-headed attention on the wrong axis of the matrix. I’ve uploaded a new video where I’ve added some text to explain this now.
@jeremy btw the video embedded in Practical Deep Learning for Coders - 24: Attention & transformers doesn’t work. My guess is that the embedded link is wrong, currently it is:
src="https://www.youtube-nocookie.com/embed/https://www.youtube.com/watch?v=DH5bp6zTPB4?modestbranding=1"
it should be
src="https://www.youtube-nocookie.com/embed/DH5bp6zTPB4?modestbranding=1"
Update on rearrange and torch.compile:
einops 0.6.1 added torch.compile support. If you use an einops layer (Rearrange) it will work out of the box. If you use an einops function (rearrange) as Jeremy does in the lesson, then you still need to register the function to prevent it from breaking the graph. However, einops now has a function to do this automatically:
from einops._torch_specific import allow_ops_in_compiled_graph
allow_ops_in_compiled_graph()
For anyone that got this error: ImportError: cannot import name ‘AttentionBlock’ from ‘diffusers.models.attention’
Apparently AttentionBlock has been replaced by just Attention source
try this: from diffusers.models.attention import Attention as AttentionBlock
But the results won’t be the same because they seem to have changed how the class works.
Thanks for another great lesson!
I’m a little confused by the timestep embeddings. What motivates them? What Is the advantage of supplying them to the model instead of , for example, simply supplying the alphabar/t/some other scalar which indicates where on the noising schedule we are?
My best guess is that we want to pass as rich a representation of the degree of noise as possible to give the MLP that takes in the timestep embeddings the opportunity to learn something useful. I’m guessing the approach we implemented in this notebook of exponentiating/scaling and then applying sine/cosine is fairly arbitrary and we could come up with a bunch of similar approaches.
Thanks!
I wanted to share a small insight I had. Jeremy might have explained this but, if so, I wasn’t paying attention and had to learn this painfully, through trial-and-error.
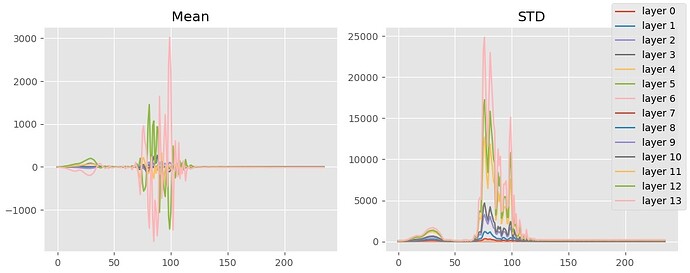
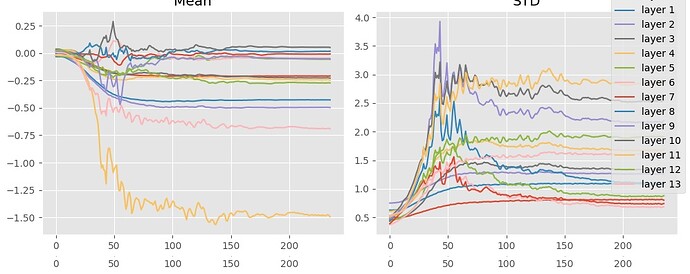
Notice that Jeremy doesn’t use Kaiming initialization when training the diffusion U-net. If you do so, the model converges on a loss of 1 for a while before it’s able to find a more optimal solution.
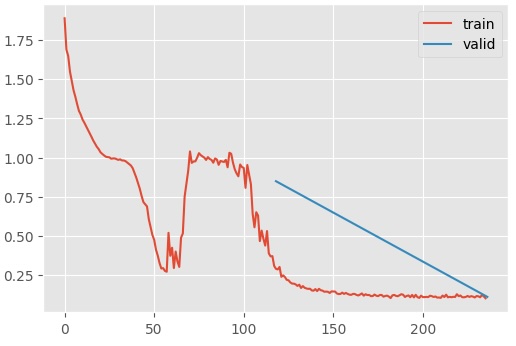
Plotting the summary statistics of the output of the resblocks, you’ll notice that this “phase shift” (is there a better word for this?) occurs when the means converge on 0. Before then, the means and standard deviations are all over the place.
I concluded that the model first has to learn a mechanism to compensate for extremely large activations before it can meaningfully fit to the epsilons. Why?
My insight arrived when I tried to the following: if you do not use Kaiming, then the loss/time curve is quite smooth.
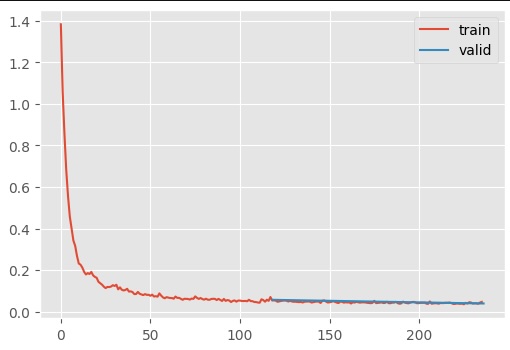
The summary statistics also look quite reasonable.
Why does Kaiming initialization result in this bizarre training dynamic? Keep in mind that Kaiming is designed to reduce to variance to 1 when the output of a neural network is expected to be only non-negatives, due to the ReLU activation function. However, a preactiviation res block does not apply ReLU to the residual link. In other words, we expect the output to have roughly unit-variance by default. Therefore, the default initialization is more appropriate to ensure that the activation magnitudes do not increase throughout forward propagation.
The embeddings in this lesson is a little different from the imdb movie database, isnt it? They’re not nn.Parameters like in the previous lesson. They’re not subject to gradient-descent+step; they’re just fixed numbers. Am I right?
Update: ok, I realised my mistake: they’re fixed numbers that’s passed into a bunch of linear layers in EmbUNetModel.emb_mlp(). To summarise, they’re some [timescale numbers] → MLP → ResNet
Sorry for that.
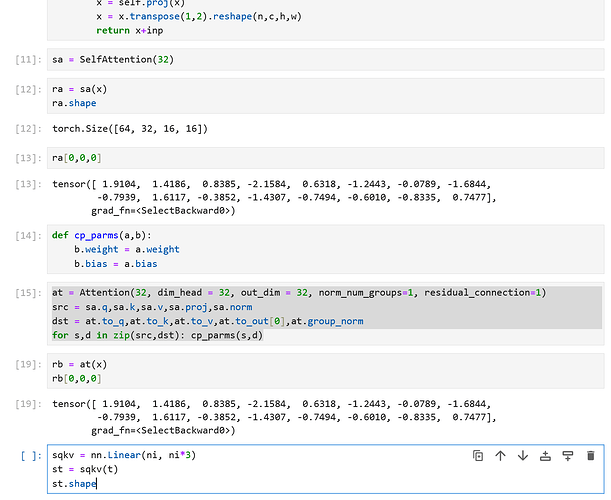
Hey guys, here’s a fix for the changed AttentionBlock:
Change Cell #3 to:
from diffusers.models.attention import Attention
And change the copying function to the following:
at = Attention(32, dim_head = 32, out_dim = 32, norm_num_groups=1, residual_connection=1)
src = sa.q,sa.k,sa.v,sa.proj,sa.norm
dst = at.to_q,at.to_k,at.to_v,at.to_out[0],at.group_norm
for s,d in zip(src,dst): cp_parms(s,d)
Finally, the numbers should match:
That was very useful, thanks