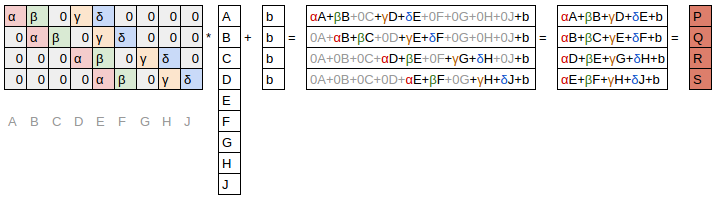
I couldn’t really grasp this concept of “wasting calculations” Jeremy talked about when answering the question at (1:16:00). Would someone mind to elaborate about it a little more or point to a resource? I feel its a relevant concept to understand convolutions better.
How Convolutions Work: A Mini-Review
Consider the model specified by this call to get_cnn_model():
def get_cnn_model(data):
return nn.Sequential(
Lambda(mnist_resize), # 28x28 input layer
nn.Conv2d( 1, 8, 5, padding=2,stride=2), nn.ReLU(), # 8x14x14 first convolution layer
nn.Conv2d( 8,16, 3, padding=1,stride=2), nn.ReLU(), # 16x7x7 second convolution layer
nn.Conv2d(16,32, 3, padding=1,stride=2), nn.ReLU(), # 32x4x4 third convolution layer
nn.Conv2d(32,32, 3, padding=1,stride=2), nn.ReLU(), # 32x2x2 fourth convolution layer
nn.AdaptiveAvgPool2d(1), # 32x1x1 adaptive average pooling layer
Lambda(flatten), # 32x1 flatten
nn.Linear(32,data.c) # 10x1 output layer
)
Let’s consider the first convolution layer. The inputs to nnConv2d specify 1 input channel, 8 output channels, a 5\times5 kernel, zero-padding of 2 pixels, and a stride length of 2. Now the input image is 28\times28, and with 2 pixels of padding on each side the image array becomes 32\times32.
If we line up a 5\times5 kernel at an initial position at the top left of this image, then column 5 of the kernel lines up with column 5 of the image, and row 5 of the kernel lines up with row 5 of the image. Sliding the kernel rightwards across the image in steps (stride) of 2 pixels until there is no more room to slide yields a total of (32-5)//2 + 1 = 14 kernel positions, including the initial one. This is the size of the output matrix of the convolution.
We can generalize this formula for the convolution output size: when a (square) convolution kernel of size n_{kernel } is applied to a (square) array of size n_{input}, using padding of n_{pad} pixels and stride of n_{stride} pixels, the size of the (square) output matrix is
n_{out} = (n_{in}+ 2\times n_{pad} - n_{kernel} )//{n_{stride}} +1,
where // represents the floor division operation.
By the same reasoning, since the image is square, starting from the initial position and sliding the kernel downwards across the image in steps of 2 pixels, again yields 14 kernel positions.
At each of the 14\times14 kernel positions, the kernel is ‘applied’ on the overlapping 5\times5 portion of the image by multiplying each pixel value by its corresponding kernel array value. We sum these 5\times5=25 products to obtain a single scalar value, which is the pixel value at this position.
How many weights do we need to fit in this layer? The convolution kernel is 5\times5, and we need a different kernel for each of the 8 output channels. So altogether there are 5\times5\times8 = 200 weights to determine for the first layer, assuming the bias vector is all zeros.
The output of the first layer is a stack of 8 channels of 14\times14 arrays, which is a 8\times14\times14 array, which has 1568 entries.
How many parameters are needed for this model? Start with the convolution layers: 5\times5\times8 = 200 for the first, 3\times3\times16 = 144 for the second, 3\times3\times32 = 288 for the third, 3\times3\times32 = 288 for the fourth. The total for the convolution layers is 200 + 144 + 288 + 288 = 920 parameters. The final fully connected linear layer maps the vector of 32 values returned by the AdaptiveAveragePool layer to the vector of 10 output parameters. This mapping requires a 32\times10 matrix, which has 320 parameters. The AdaptiveAvgPool and Lambda (flatten) layers have no parameters to solve. So the model has to determine a total number of 920 + 320 = 1240 parameters. Recall that for this calculation we have ignored bias parameters. The number of input data points for each example is 28\times28=784, and there are over 50,000 training examples, so the number of data points is vastly larger than the number of parameters!
Now test your understanding by working out the sizes of the remaining layers and checking against the answers provided in the comments to get_cnn_model()!
Thanks @simonjhb, good catch! I should’ve said “variance is defined for many useful distributions other than the Gaussian”.
@jcatanza this seems to be cross-posted. Can you please delete this one?
Yes. Done.
During https://youtu.be/HR0lt1hlR6U?t=4272 why going from 27 channels to 32 is losing information? The increase in channel numbers should instead preserve the information.
Understood now.
I think you’re refering to this image in lesson 6:
from this post: CNNs from different viewpoints. For beginners | by Matt Kleinsmith | ImpactAI | Medium
This is the image I had in the head to help me understand what was Jeremy talking about in Lesson 10.
I’ll digg deeper into this unfold function.
I felt frustrated that we hadn’t yet implemented from scratch a Conv2d layer like we did for the Linear Layer.
But maybe it would have taken too long on the course.
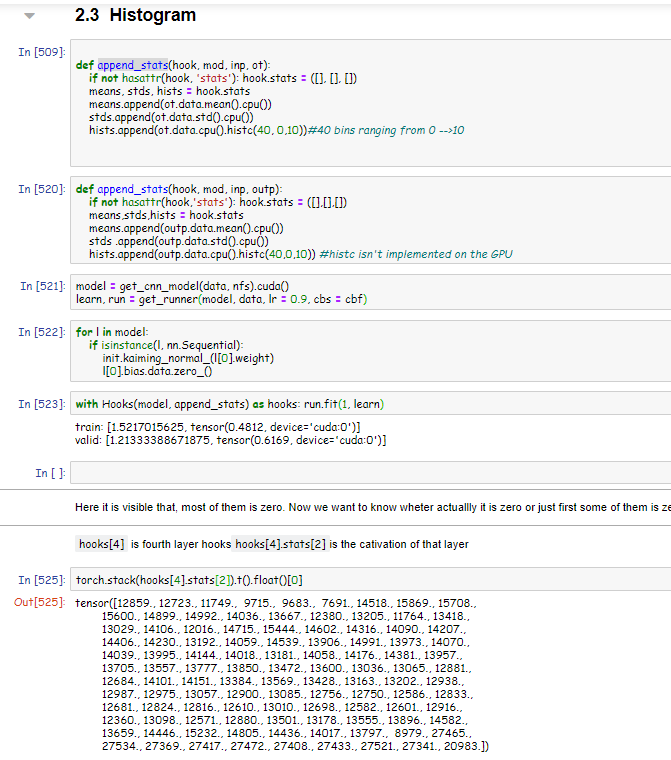
I don’t know where I am making mistakes. In append_stats function I already defined that output should be devided into 40 beans and value ranges from 0 to 10. After that, I tried to see what are actual activation in first 2 bins. As in the video it is said that, all first two bins have the value nearly 0. But my activations are huge value. They are far greater than Zero. Then I went to actual notebook and run it to see, if there is any mistakes I have done during reproducing the notebook. But the activations are also huge there. Does anyone faced such problem? Or It’s me not getting something.
Here is the code snippet and output activationIn lesson 11, Jeremy showed us that Binomial is better choice for activation function when the images have more than one objects in them (or sometimes none of them). I wanted to ask what is the right process of deciding a threshold value when using binomial activation, since the values don’t add up to 1 in this case
First of all Jeremy actually meant binary cross-entropy when he said binomial.
Threshold value is a hyperparameter so the best way to choose it is to try a few values and see which one is optimal, i.e. gets best classification accuracy. You should probably start by applying the same threshold value for all classes. Of course optimal is in the eye of the experimenter. You might place different weights on correct classification for each of the classes.
Also, I think that threshold values could be set independently for each class. Someone please correct me if I’m wrong.
Would it be wise to scale the outputs of a binary activation function, (like normalising)?
Hi all,
I was trying to write my own code based on Jeremy’s 06_cuda_cnn_hooks_init notebook.
It was going fairly ok until I stumbled upon a piece of code that while listening to the video seems very ordinary but trying to replicate made me think and get lost!
Here, to get the telemetry Jeremy used the following class:
class SequentialModel(nn.Module):
def __init__(self, *layers):
super().__init__()
self.layers = nn.ModuleList(layers)
self.act_means = [[] for _ in layers]
self.act_stds = [[] for _ in layers]
def __call__(self, x):
for i,l in enumerate(self.layers):
x = l(x)
self.act_means[i].append(x.data.mean())
self.act_stds [i].append(x.data.std ())
return x
def __iter__(self): return iter(self.layers)
I understand after running the code that act_means is a 2d list that stores data for every layer. For instance, act_means[0] will store data (means) for layer 0 and so on until layer 7.
Next, when I look at code in the call function, I notice that x.data.mean() is being stored. Now I see running this code results in 216 values for the second dimension of the list.
len(model.act_means)
results in 7 which is understandable.
However,
len(model.act_means[0])
resulted in 216.
What is the math behind this 216, in terms of how did we get this and what does this actually mean from a conceptual perspective?
I thought to break it into simple scenario by picking one image and passing through Conv2d followed by ReLU:
# Create 2 layers (Conv2d and ReLU)
conv_layer = nn.Conv2d(1,8,5)
relu_layer = nn.ReLU()
# Get 1 image from databunch
image = dataBunch.train_ds.x[0].view(28,28)
# Pass this image through Conv2d and ReLU
output = relu_layer(conv_layer(image.view(-1,1,28,28)))
# Get the output
output.data.shape #torch.Size([1, 8, 24, 24])
# Get the mean
output.data.mean() #tensor(0.1526)
Taking mean() of this output.data results as expected in a single number so not getting why 216 columns are needed for the list?
I am sure I am missing something fundamental over here so appreciate your guidance ![]()
Regards,
Dev.
Still stuck here… any inputs?
@jcatanza Based on your previous posts, I thought you tried out these code pieces yourself. Trying my luck by tagging you… 
Can someone explain the part where we choose the kernel size to be 5x5 in the first layer and 3x3 on the rest of the network, or corespondingly 7x7 in imagenet models, and why we are losing information when we choose a 3x3 kernel size on imagenet models?
Hi @devtastic
The dimension is 216 because in the notebook when run.fit is called after this cell, the network trains for 216 iterations and so you have self.act_means[i].append(x.data.mean()) being called 216 times. This simply results in 216 means being added to the list.
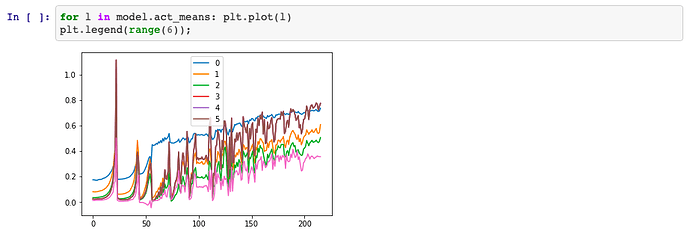
This graph pretty much confirms this: (the X-Axis has a length of about 216)
Hello @akashpalrecha ,
I understand fit is called after this line, but why the number 216? Batch size is set to 512 in the beginning… so how does 216 come up?
Not getting it still, sorry!
@devtastic, you do not need to apologize, it’s a good habit to ask for help.
Now back to your question.
Here’s what’s happening, plain and simple:
- The model starts to train.
- In each forward pass/training iteration, the
appendfunction is called and the mean ofx.datais appended to the listself.act_means[i]for each layer. -
x.data.mean()happens to be a SINGLE number. - The network trains for
216iterations, and so216forward passes, and hence you get216numbers appended to those lists.
That’s it!
Thanks again @akashpalrecha.
That’s exactly my confusion point - how/where does the model know to run 216 forward passes / iterations? Why not any other number?
That comes from the data loader objects.
The training data loader object acts as an Iterator in our training loop inside the fit function. The for loop ends where the iterator reaches the end of it’s cycle. In this case the that’s exactly where the training data is exhausted. And the number of training batches our data loader is able to spit out before it runs out happens to be 108, and since you have 2 epochs in the run.fit call, you get 216 (108*2) iterations.
You should try and investigate the fit function to get a better idea.
Also, try running this:
for i, _ in enumerate(data.train_dl): print(i)
You should get 108.