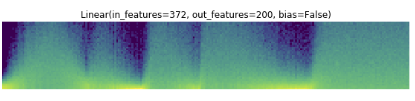
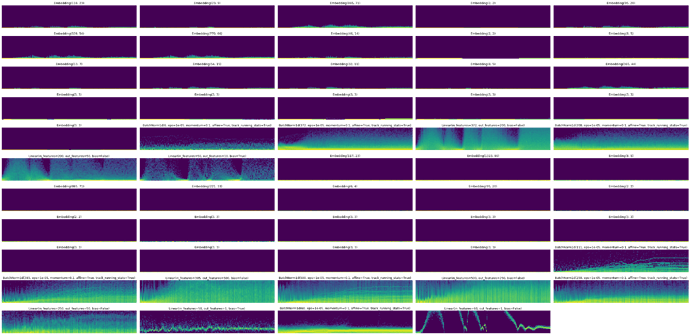
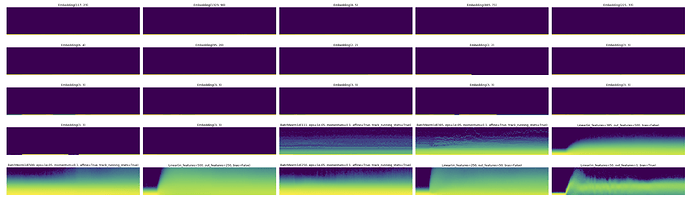
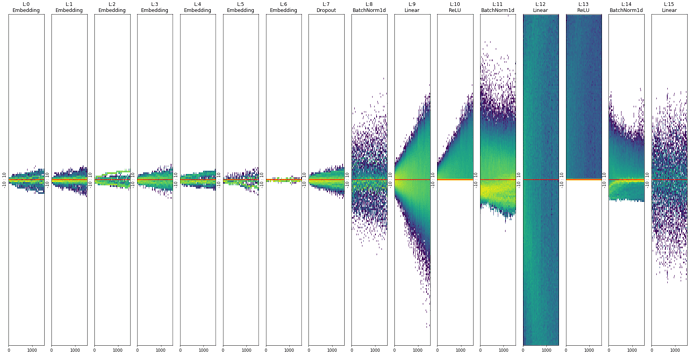
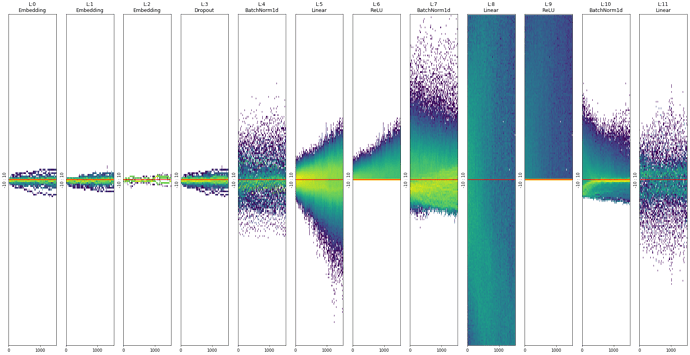
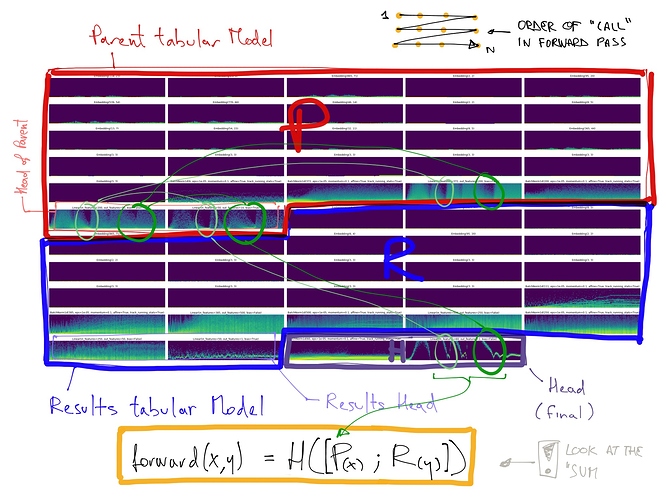
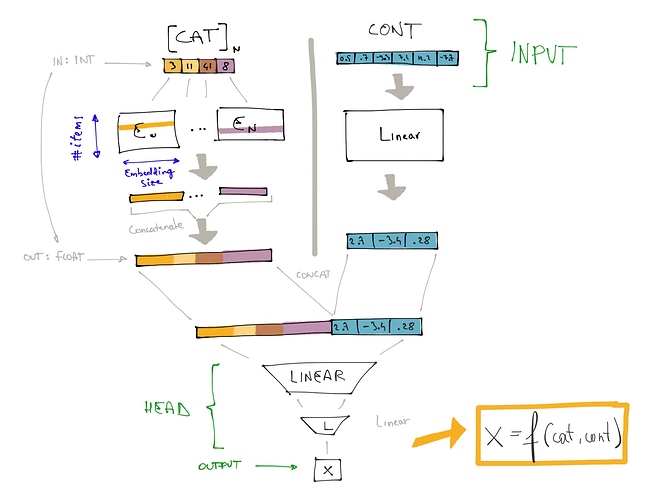
Thanks for the app name! Sorry I am at work, so I did those graph during lunch:
self.results (the TabularModel responsible to get the questionnaire into a feature vector)
Then self.questions, the TabularModel called in a loop (one time for each questionnaire in the batch). We pass a batch of questions in this model). Replaced the BatchNorm by LayerNorm here:
self.attn, the MultiHeadSelfAttention layer. It doesn’t seem to be learning anything right now… Still have to figure this out.
Then self.head which is responsible to predict the final prediction… I am confused, there doesn’t seem to be a lot of activities there:
Here is the updated code for my mode, using attention:
results_emb_szs = get_emb_sz(results_tab)
questions_emb_szs = get_emb_sz(questions_tab)
class ParentChildModel(Module):
def __init__(self):
self.results = TabularModel(results_emb_szs, len(results_cont_names), 64, [512, 256], ps=[0.01, 0.1], embed_p=0.04, bn_final=True)
self.questions = QuestionModel(questions_emb_szs, len(questions_cont_names), 1, layers=[512, 256, 64], ps=[0.01, 0.1, .1], embed_p=0.04, y_range=[-1,101])
self.attn = MultiHeadAttention(1, 64, 64, 64)
self.head = nn.Sequential(*[LinBnDrop(128, 1, p=0., bn=True), SigmoidRange(*[-1, 101])])
for p in self.parameters():
if p.dim() > 1:
nn.init.kaiming_uniform_(p)
def forward(self, data, children):
parent_cat, parent_cont = data[0], data[1]
results = self.results(parent_cat, parent_cont)
questionScores = []
batchQuestionMid = []
lengths = []
for children_cat, children_cont, length in children:
result, mid = self.questions(children_cat[:length], children_cont[:length])
result = result.squeeze()
lengths += [length]
batchQuestionMid += [F.pad(mid, pad=(0, 0, 0,children_cat.shape[0]-len(mid)), mode='constant', value=1e-7)]
questionScores += [F.pad(result, pad=(0,1000-len(result)), mode='constant', value=1e-7)]
lengths = torch.cat(lengths)
batchQuestionMid = torch.stack(batchQuestionMid)
mask = torch.arange(batchQuestionMid.shape[1]).repeat((batchQuestionMid.shape[0],1)).to(lengths.device) < lengths[:, None]
mask = mask.unsqueeze(-1)
batchQuestionMid, attention = self.attn(batchQuestionMid, batchQuestionMid, batchQuestionMid, mask)
mid_merged = batchQuestionMid.sum(axis=1)
concat = torch.cat([results, mid_merged], axis=1)
results = self.head(concat)
questionScores = torch.stack(questionScores, dim=0)
return results, questionScores
And a more complete export of the structure of the model:
ParentChildModel(
(results): TabularModel(
(embeds): ModuleList(
(0): Embedding(123, 24)
(1): Embedding(24, 9)
(2): Embedding(877, 71)
(3): Embedding(2, 2)
(4): Embedding(99, 21)
(5): Embedding(549, 55)
(6): Embedding(782, 67)
(7): Embedding(46, 14)
(8): Embedding(2, 2)
(9): Embedding(8, 5)
(10): Embedding(13, 7)
(11): Embedding(54, 15)
(12): Embedding(32, 11)
(13): Embedding(8, 5)
(14): Embedding(365, 44)
(15): Embedding(3, 3)
(16): Embedding(3, 3)
(17): Embedding(3, 3)
(18): Embedding(3, 3)
(19): Embedding(3, 3)
(20): Embedding(3, 3)
)
(emb_drop): Dropout(p=0.04, inplace=False)
(bn_cont): BatchNorm1d(6, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(layers): Sequential(
(0): LinBnDrop(
(0): BatchNorm1d(376, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(1): Dropout(p=0.01, inplace=False)
(2): Linear(in_features=376, out_features=512, bias=False)
(3): ReLU(inplace=True)
)
(1): LinBnDrop(
(0): BatchNorm1d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(1): Dropout(p=0.1, inplace=False)
(2): Linear(in_features=512, out_features=256, bias=False)
(3): ReLU(inplace=True)
)
(2): LinBnDrop(
(0): BatchNorm1d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(1): Linear(in_features=256, out_features=64, bias=False)
)
)
)
(questions): QuestionModel(
(embeds): ModuleList(
(0): Embedding(122, 24)
(1): Embedding(1339, 90)
(2): Embedding(8, 5)
(3): Embedding(877, 71)
(4): Embedding(224, 33)
(5): Embedding(6, 4)
(6): Embedding(99, 21)
(7): Embedding(2, 2)
(8): Embedding(2, 2)
(9): Embedding(3, 3)
(10): Embedding(3, 3)
(11): Embedding(3, 3)
(12): Embedding(3, 3)
(13): Embedding(3, 3)
(14): Embedding(3, 3)
(15): Embedding(3, 3)
)
(emb_drop): Dropout(p=0.04, inplace=False)
(bn_cont): LayerNorm((110,), eps=1e-05, elementwise_affine=True)
(layers): Sequential(
(0): LinLnDrop(
(0): LayerNorm((383,), eps=1e-05, elementwise_affine=True)
(1): Dropout(p=0.01, inplace=False)
(2): Linear(in_features=383, out_features=512, bias=False)
(3): ReLU(inplace=True)
)
(1): LinLnDrop(
(0): LayerNorm((512,), eps=1e-05, elementwise_affine=True)
(1): Dropout(p=0.1, inplace=False)
(2): Linear(in_features=512, out_features=256, bias=False)
(3): ReLU(inplace=True)
)
(2): LinLnDrop(
(0): LayerNorm((256,), eps=1e-05, elementwise_affine=True)
(1): Dropout(p=0.1, inplace=False)
(2): Linear(in_features=256, out_features=64, bias=False)
(3): ReLU(inplace=True)
)
)
(layers2): Sequential(
(0): LinLnDrop(
(0): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
(1): Linear(in_features=64, out_features=1, bias=False)
)
(1): SigmoidRange(low=-1, high=101)
)
)
(attn): MultiHeadAttention(
(w_qs): Linear(in_features=64, out_features=64, bias=False)
(w_ks): Linear(in_features=64, out_features=64, bias=False)
(w_vs): Linear(in_features=64, out_features=64, bias=False)
(fc): Linear(in_features=64, out_features=64, bias=False)
(attention): ScaledDotProductAttention(
(dropout): Dropout(p=0.1, inplace=False)
)
(dropout): Dropout(p=0.1, inplace=False)
(layer_norm): LayerNorm((64,), eps=1e-06, elementwise_affine=True)
)
(head): Sequential(
(0): LinBnDrop(
(0): BatchNorm1d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(1): Linear(in_features=128, out_features=1, bias=False)
)
(1): SigmoidRange(low=-1, high=101)
)
)