Hi All,
There was a lot of material covered for lesson9. There’s a copy of the notes on my github : https://github.com/timdavidlee/fast_dl2
Otherwise, hope the notes are helpful.
[Update, i actually hit the character limit, so I’ve truncated some of the notes]
[Update: 4/8, applied jeremy’s edits]
Tim
%matplotlib inline
%reload_ext autoreload
%autoreload 2
import sys
sys.path.append('../')
from fastai.conv_learner import *
from fastai.dataset import *
from pathlib import Path
import json
from PIL import ImageDraw, ImageFont
from matplotlib import patches, patheffects
# check to make sure you set the device
torch.cuda.set_device(0)
Welcome to Lecture 9
Last Week: Largest Item Classifier
Last Week: Bbox only
Let’s Continue start with Single Object detecion
Load the data from last week, and global keys
-
PATH- is the location of the dataset -
JPEGS- images -
CSV- filenames and categorical labels
PATH = Path('data/pascal')
JPEGS = 'VOCdevkit/VOC2007/JPEGImages'
CSV = PATH/'tmp/lrg.csv'
IMAGES,ANNOTATIONS,CATEGORIES = ['images', 'annotations', 'categories']
FILE_NAME,ID,IMG_ID,CAT_ID,BBOX = 'file_name','id','image_id','category_id','bbox'
Show image function
def show_img(im, figsize=None, ax=None):
if not ax: fig,ax = plt.subplots(figsize=figsize)
ax.imshow(im)
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
return ax
-
bb_hw= Convenience Function to swap the order of the coordinates (See lesson 8) -
draw_outline= adds a black border around any line. This ensures we can read it regardless of whether the background is light or dark. -
draw_rect= draw the bounding rectangle -
draw_text= write the text category on the image
def bb_hw(a): return np.array([a[1],a[0],a[3]-a[1],a[2]-a[0]])
def draw_outline(o, lw):
o.set_path_effects([patheffects.Stroke(
linewidth=lw, foreground='black'), patheffects.Normal()])
def draw_rect(ax, b):
patch = ax.add_patch(patches.Rectangle(b[:2], *b[-2:], fill=False, edgecolor='white', lw=2))
draw_outline(patch, 4)
def draw_text(ax, xy, txt, sz=14):
text = ax.text(*xy, txt,
verticalalignment='top', color='white', fontsize=sz, weight='bold')
draw_outline(text, 1)
Load the 2007 training data in the json format
trn_j = json.load((PATH/'pascal_train2007.json').open())
trn_fns = dict((o[ID], o[FILE_NAME]) for o in trn_j[IMAGES])
cats = dict((o[ID], o['name']) for o in trn_j[CATEGORIES])
Our image data
trn_j.keys()
dict_keys(['images', 'type', 'annotations', 'categories'])
ID to picture file name
trn_fns[12]
'000012.jpg'
BB_CSV = PATH/'tmp/bb.csv'
Load the resnet model
f_model=resnet34
sz=224
bs=64
val_idxs = get_cv_idxs(len(trn_fns))
create transformations and image dataset:
-
sz= image size -
crop_type= this case we will not crop the image, since we might cut off objects we need to recognize around the edges, but it will ‘squish’ it into a square shape, since this is required by fastai( for now at least). -
tfm_y= this is the y transformation that will be adjusted
Objects:
-
tfms= transformations to apply -
md= dataset has the bounding box information -
md2= transformations to has the actual categorical labelings
tfms = tfms_from_model(f_model, sz, crop_type=CropType.NO, tfm_y=TfmType.COORD)
md = ImageClassifierData.from_csv(PATH, JPEGS, BB_CSV, tfms=tfms,
continuous=True, val_idxs=val_idxs)
md2 = ImageClassifierData.from_csv(PATH, JPEGS, CSV, tfms=tfms_from_model(f_model, sz))
Let’s make a custom Datasets that will have a 2nd set of labels
The custom dataset will have the following structure:
**(md) Image - (md)Bounding Box - (md2) Label **
Note that the __getitem__() will return a concatenated tuple:
(x, (y1, y2))
def __getitem__(self, i):
x,y = self.ds[i]
return (x, (y,self.y2[i]))
class ConcatLblDataset(Dataset):
def __init__(self, ds, y2): self.ds,self.y2 = ds,y2
def __len__(self): return len(self.ds)
def __getitem__(self, i):
x,y = self.ds[i]
return (x, (y,self.y2[i]))
Create training and test sets
trn_ds2 = ConcatLblDataset(md.trn_ds, md2.trn_y)
val_ds2 = ConcatLblDataset(md.val_ds, md2.val_y)
The image
val_ds2[0][0]
array([[[ 0.39125, 0.43014, 0.48172, ..., 0.17518, 0.32367, 0.40783],
[ 0.51636, 0.44973, 0.59202, ..., 0.17386, 0.23164, 0.36722],
[ 0.54416, 0.57267, 0.70099, ..., 0.05768, 0.2232 , 0.35455],
...,
[ 1.46039, 1.50291, 1.5195 , ..., 0.7803 , 0.56716, -0.63922],
[ 0.93739, 1.021 , 1.15993, ..., 1.12806, 1.08947, 0.45857],
[ 0.58584, 0.45245, 0.29605, ..., 1.00028, 0.92495, 0.82729]],
[[ 0.24041, 0.31444, 0.41422, ..., 0.33162, 0.47052, 0.54764],
[ 0.39737, 0.42156, 0.57304, ..., 0.33887, 0.38799, 0.52038],
[ 0.52462, 0.58245, 0.67485, ..., 0.2519 , 0.40003, 0.51502],
...,
[ 1.47208, 1.50185, 1.50771, ..., 0.60917, 0.44337, -0.73978],
[ 0.84169, 0.94566, 1.06783, ..., 0.97373, 1.01637, 0.39674],
[ 0.47731, 0.36442, 0.1823 , ..., 0.85592, 0.85008, 0.75529]],
[[ 0.63094, 0.76758, 0.91924, ..., 0.46997, 0.58218, 0.63571],
[ 0.86685, 0.89343, 1.08916, ..., 0.4597 , 0.4921 , 0.60825],
[ 0.96684, 1.00092, 1.07853, ..., 0.35109, 0.50631, 0.63579],
...,
[ 1.56056, 1.59266, 1.60554, ..., 0.54531, 0.38118, -0.79327],
[ 0.92625, 1.02055, 1.14452, ..., 0.91826, 0.93747, 0.31286],
[ 0.56966, 0.44559, 0.26428, ..., 0.8008 , 0.77093, 0.67405]]], dtype=float32)
The Bounding box and category
val_ds2[0][1]
(array([ 0., 49., 205., 180.], dtype=float32), 14)
Replace the md dataset with the new 2 labeled dataset
md.trn_dl.dataset = trn_ds2
md.val_dl.dataset = val_ds2
We have to denormalize the images from the dataloader before they can be plotted.
x,y=next(iter(md.val_dl))
ima=md.val_ds.ds.denorm(to_np(x))[1]
b = bb_hw(to_np(y[0][1])); b
array([ 1., 63., 222., 159.], dtype=float32)
ax = show_img(ima)
draw_rect(ax, b)
draw_text(ax, b[:2], md2.classes[y[1][1]])

Add a custom head to the end of resnet34
We need one output activation for each class (for its probability) plus one for each bounding box coordinate. We’ll use an extra linear layer this time, plus some dropout, to help us train a more flexible model.
head_reg4 = nn.Sequential(
Flatten(),
nn.ReLU(),
nn.Dropout(0.5),
nn.Linear(25088,256),
nn.ReLU(),
nn.BatchNorm1d(256),
nn.Dropout(0.5),
nn.Linear(256,4+len(cats)),
)
models = ConvnetBuilder(f_model, 0, 0, 0, custom_head=head_reg4)
learn = ConvLearner(md, models)
learn.opt_fn = optim.Adam
Definte a Loss, L1 regularization, and Accuracy helper functions
Loss function
-
bb_i = F.sigmoid(bb_i)*224- force the value between 0 and 1 (times 224). This is to force the data into a specific range of values - Where to put
batch_norm? Recommended to put it after relu, so you keep the ability to make negative numbers. -
L1 loss + Cross Entropy Loss=F.l1_loss(bb_i, bb_t) + F.cross_entropy(c_i, c_t)*20. Thex20is approximated to ensure that the two losses are on the same scale
def detn_loss(input, target):
bb_t,c_t = target
bb_i,c_i = input[:, :4], input[:, 4:]
bb_i = F.sigmoid(bb_i)*224
# I looked at these quantities separately first then picked a multiplier
# to make them approximately equal
return F.l1_loss(bb_i, bb_t) + F.cross_entropy(c_i, c_t)*20
def detn_l1(input, target):
bb_t,_ = target
bb_i = input[:, :4]
bb_i = F.sigmoid(bb_i)*224
return F.l1_loss(V(bb_i),V(bb_t)).data
def detn_acc(input, target):
_,c_t = target
c_i = input[:, 4:]
return accuracy(c_i, c_t)
learn.crit = detn_loss
learn.metrics = [detn_acc, detn_l1]
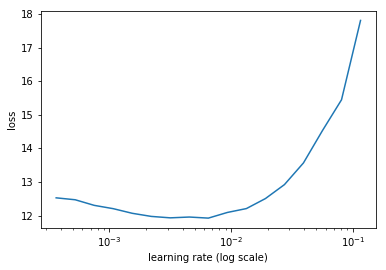
With the metrics defined, we find the learning rate
learn.lr_find()
learn.sched.plot()
97%|█████████▋| 31/32 [00:09<00:00, 3.19it/s, loss=524]
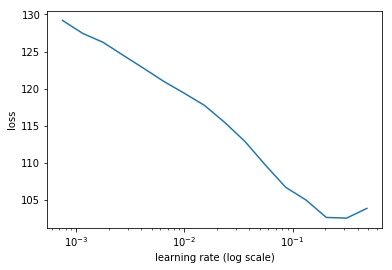
Set the rate
lr=1e-2
Fit the Model
learn.fit(lr, 1, cycle_len=3, use_clr=(32,5))
epoch trn_loss val_loss detn_acc detn_l1
0 73.80378 43.574409 0.813852 31.699385
1 51.747788 37.229919 0.819561 25.624957
2 41.568981 35.318695 0.82497 24.513911
[35.318695, 0.8249699547886848, 24.51391077041626]
Save our Model
learn.save('reg1_0')
Freeze everything except the last two layers
learn.freeze_to(-2)
#### Setting learning rates
lrs = np.array([lr/100, lr/10, lr])
learn.lr_find(lrs/1000)
learn.sched.plot(0)
91%|█████████ | 29/32 [00:08<00:00, 3.36it/s, loss=230]
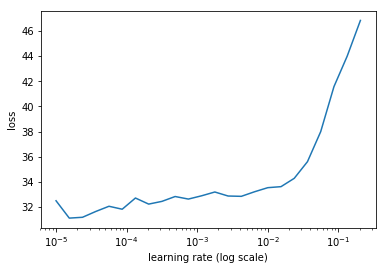
learn.fit(lrs/5, 1, cycle_len=5, use_clr=(32,10))
epoch trn_loss val_loss detn_acc detn_l1
0 18.630316 36.514301 0.791466 21.233154
1 19.990961 33.011433 0.81881 20.244233
2 18.506014 31.954967 0.820763 19.621269
3 16.846955 31.920164 0.81881 19.204269
4 15.234001 31.665308 0.819261 18.943963
[31.665308, 0.8192608207464218, 18.943962812423706]
learn.save('reg1_1')
learn.load('reg1_1')
learn.unfreeze()
learn.fit(lrs/10, 1, cycle_len=10, use_clr=(32,10))
epoch trn_loss val_loss detn_acc detn_l1
0 13.102859 30.631477 0.817758 18.990284
1 13.380544 32.969467 0.810397 19.570258
2 13.436793 32.149635 0.821214 19.051544
3 12.934334 31.497986 0.83729 18.988035
4 12.444968 32.228378 0.819261 18.880555
5 11.878257 32.434448 0.809044 18.574428
6 11.490413 31.936653 0.822716 18.974106
7 10.877252 31.002441 0.832933 18.324932
8 10.552304 30.984261 0.832933 18.481523
9 10.308766 31.074959 0.81881 18.369649
[31.074959, 0.8188100978732109, 18.369649052619934]
learn.save('reg1')
learn.load('reg1')
y = learn.predict()
x,_ = next(iter(md.val_dl))
Big Idea
Figuring out what hte main object in an image is, that is the difficult task. Finding the bounding box is the easier part. So a model that has two do both, the tasks inform each other since they share some concept together. As a result, they should share some of the layers of the network together.
from scipy.special import expit
fig, axes = plt.subplots(3, 4, figsize=(12, 8))
for i,ax in enumerate(axes.flat):
ima=md.val_ds.ds.denorm(to_np(x))[i]
bb = expit(y[i][:4])*224
b = bb_hw(bb)
c = np.argmax(y[i][4:])
ax = show_img(ima, ax=ax)
draw_rect(ax, b)
draw_text(ax, b[:2], md2.classes[c])
plt.tight_layout()
Clipping input data to the valid range for imshow with RGB data ([0..1] for floats or [0..255] for integers).
Checkout the Multi Label Classification
The notebook is posted link
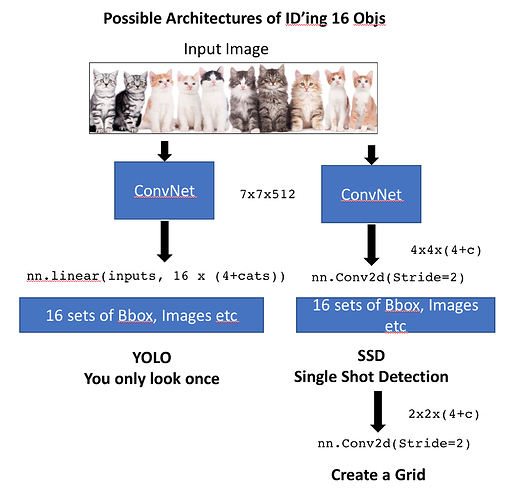
Finding multiple objects in a picture
Using the SSD Approach, we will now have a grid
So each Conv quadrant will be responsible for each part of the image. Why do we want each Convolution to be responsible for each part of the image? A concept called receptive field. Throughout your convolution layers, each piece of your tensor, has a receptive field.
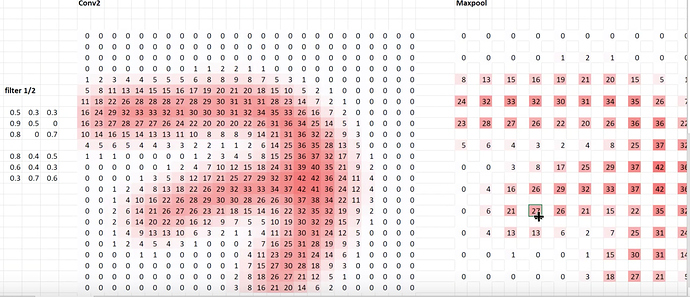
Let’s look at Microsoft Excel
Our image went through a 3x3 kernel (right)
Created a two channel output
Then went through another channel output into max pooling (sparse area)
If we trace one of the maxpool steps (pretend its a Conv2D stride 2 layer) backwards:
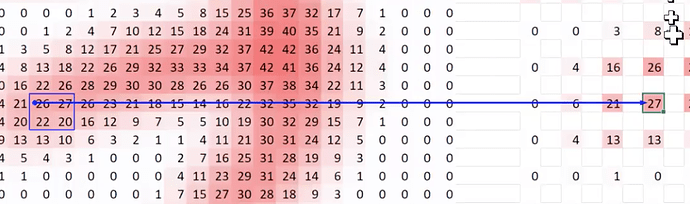
Tracing back even farther:
Tracing back to the source image:
The pixels in the middle have a lot of connections, and the edges don’t have as many. The center of the box has more dependencies. This is critically important for understanding convolution receptive fields.
%matplotlib inline
%reload_ext autoreload
%autoreload 2
import sys
sys.path.append('../')
from fastai.conv_learner import *
from fastai.dataset import *
from pathlib import Path
import json
from PIL import ImageDraw, ImageFont
from matplotlib import patches, patheffects
# check to make sure you set the device
torch.cuda.set_device(0)
Setup Globals
PATH = Path('data/pascal')
trn_j = json.load((PATH / 'pascal_train2007.json').open())
IMAGES,ANNOTATIONS,CATEGORIES = ['images', 'annotations', 'categories']
FILE_NAME,ID,IMG_ID,CAT_ID,BBOX = 'file_name','id','image_id','category_id','bbox'
cats = dict((o[ID], o['name']) for o in trn_j[CATEGORIES])
trn_fns = dict((o[ID], o[FILE_NAME]) for o in trn_j[IMAGES])
trn_ids = [o[ID] for o in trn_j[IMAGES]]
JPEGS = 'VOCdevkit/VOC2007/JPEGImages'
IMG_PATH = PATH/JPEGS
Define Common Functions (very similar to the first pascal model)
def get_trn_anno():
trn_anno = collections.defaultdict(lambda:[])
for o in trn_j[ANNOTATIONS]:
if not o['ignore']:
bb = o[BBOX]
bb = np.array([bb[1], bb[0], bb[3]+bb[1]-1, bb[2]+bb[0]-1])
trn_anno[o[IMG_ID]].append((bb,o[CAT_ID]))
return trn_anno
def show_img(im, figsize=None, ax=None):
if not ax: fig,ax = plt.subplots(figsize=figsize)
ax.imshow(im)
ax.set_xticks(np.linspace(0, 224, 8))
ax.set_yticks(np.linspace(0, 224, 8))
ax.grid()
ax.set_yticklabels([])
ax.set_xticklabels([])
return ax
def draw_outline(o, lw):
o.set_path_effects([patheffects.Stroke(
linewidth=lw, foreground='black'), patheffects.Normal()])
def draw_rect(ax, b, color='white'):
patch = ax.add_patch(patches.Rectangle(b[:2], *b[-2:], fill=False, edgecolor=color, lw=2))
draw_outline(patch, 4)
def draw_text(ax, xy, txt, sz=14, color='white'):
text = ax.text(*xy, txt,
verticalalignment='top', color=color, fontsize=sz, weight='bold')
draw_outline(text, 1)
def bb_hw(a): return np.array([a[1],a[0],a[3]-a[1],a[2]-a[0]])
def draw_im(im, ann):
ax = show_img(im, figsize=(16,8))
for b,c in ann:
b = bb_hw(b)
draw_rect(ax, b)
draw_text(ax, b[:2], cats[c], sz=16)
def draw_idx(i):
im_a = trn_anno[i]
im = open_image(IMG_PATH/trn_fns[i])
draw_im(im, im_a)
Setup Multiclass
trn_anno = get_trn_anno()
MC_CSV = PATH/'tmp/mc.csv'
mc = [set([cats[p[1]] for p in trn_anno[o]]) for o in trn_ids]
mcs = [' '.join(str(p) for p in o) for o in mc]
df = pd.DataFrame({'fn': [trn_fns[o] for o in trn_ids], 'clas': mcs}, columns=['fn','clas'])
df.to_csv(MC_CSV, index=False)
df.head()
.dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
| fn | clas | |
|---|---|---|
| 0 | 000012.jpg | car |
| 1 | 000017.jpg | person horse |
| 2 | 000023.jpg | bicycle person |
| 3 | 000026.jpg | car |
| 4 | 000032.jpg | person aeroplane |
Setup Resnet Model and Train
f_model=resnet34
sz=224
bs=64
tfms = tfms_from_model(f_model, sz, crop_type=CropType.NO)
md = ImageClassifierData.from_csv(PATH, JPEGS, MC_CSV, tfms=tfms)
learn = ConvLearner.pretrained(f_model, md)
learn.opt_fn = optim.Adam
# find learning rate
lrf=learn.lr_find(1e-5,100)
# plot the learning rate to visually choose
learn.sched.plot(0)
# select learning rate
lr = 2e-2
# fit the model
learn.fit(lr, 1, cycle_len=3, use_clr=(32,5))
epoch trn_loss val_loss <lambda>
0 1.326271 16.738022 0.394231
epoch trn_loss val_loss <lambda>
0 0.326659 0.138878 0.954184
1 0.174125 0.078377 0.973558
2 0.11821 0.074982 0.974654
[0.07498233, 0.9746544435620308]
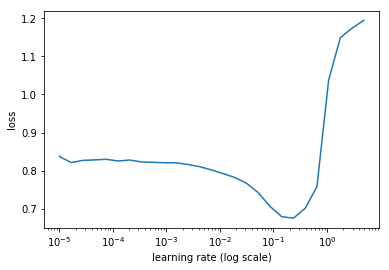
# define learning rates to search
lrs = np.array([lr/100, lr/10, lr])
# freeze the model till teh last 2 steps as before:
learn.freeze_to(-2)
# find the optimal learning rate again
learn.lr_find(lrs/1000)
learn.sched.plot(0)
# refit the model
learn.fit(lrs/10, 1, cycle_len=5, use_clr=(32,5))
81%|████████▏ | 26/32 [00:07<00:01, 3.42it/s, loss=0.33]
epoch trn_loss val_loss <lambda>
0 0.070927 0.081387 0.972078
1 0.052779 0.078058 0.974429
2 0.038978 0.078155 0.974745
3 0.027514 0.074822 0.977141
4 0.019513 0.075868 0.977652
[0.075868085, 0.9776517376303673]
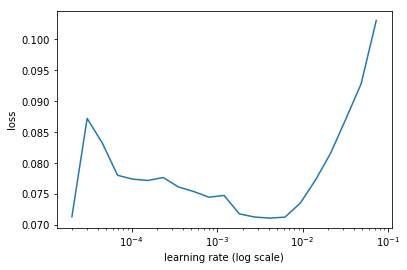
Save the model
learn.save('mclas')
learn.load('mclas')
multiple Bbox per cell
CLAS_CSV = PATH/'tmp/clas.csv'
MBB_CSV = PATH/'tmp/mbb.csv'
f_model=resnet34
sz=224
bs=64
Create Lookups and reference objects
-
mc- list of items found per image -
mcs- list of items found per image, but the ID -
id2cat- numeric value to category -
cat2id- category to id
mc = [[cats[p[1]] for p in trn_anno[o]] for o in trn_ids]
id2cat = list(cats.values())
cat2id = {v:k for k,v in enumerate(id2cat)}
mcs = np.array([np.array([cat2id[p] for p in o]) for o in mc]); mcs
array([array([6]), array([14, 12]), array([ 1, 1, 14, 14, 14]), ..., array([17, 8, 14, 14, 14]),
array([6]), array([11])], dtype=object)
# get cross validation ids
val_idxs = get_cv_idxs(len(trn_fns))
((val_mcs,trn_mcs),) = split_by_idx(val_idxs, mcs)
Create and Save multiple Bounding boxes
mbb = [np.concatenate([p[0] for p in trn_anno[o]]) for o in trn_ids]
mbbs = [' '.join(str(p) for p in o) for o in mbb]
df = pd.DataFrame({'fn': [trn_fns[o] for o in trn_ids], 'bbox': mbbs}, columns=['fn','bbox'])
df.to_csv(MBB_CSV, index=False)
df.head()
.dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
| fn | bbox | |
|---|---|---|
| 0 | 000012.jpg | 96 155 269 350 |
| 1 | 000017.jpg | 61 184 198 278 77 89 335 402 |
| 2 | 000023.jpg | 229 8 499 244 219 229 499 333 0 1 368 116 1 2 ... |
| 3 | 000026.jpg | 124 89 211 336 |
| 4 | 000032.jpg | 77 103 182 374 87 132 122 196 179 194 228 212 ... |
Setup Dataset
aug_tfms = [RandomRotate(10, tfm_y=TfmType.COORD),
RandomLighting(0.05, 0.05, tfm_y=TfmType.COORD),
RandomFlip(tfm_y=TfmType.COORD)]
tfms = tfms_from_model(f_model, sz, crop_type=CropType.NO, tfm_y=TfmType.COORD, aug_tfms=aug_tfms)
md = ImageClassifierData.from_csv(PATH, JPEGS, MBB_CSV, tfms=tfms, continuous=True, num_workers=4)
Create our Dataset with 2 associated Labels
class ConcatLblDataset(Dataset):
def __init__(self, ds, y2):
self.ds,self.y2 = ds,y2
self.sz = ds.sz
def __len__(self): return len(self.ds)
def __getitem__(self, i):
x,y = self.ds[i]
return (x, (y,self.y2[i]))
trn_ds2 = ConcatLblDataset(md.trn_ds, trn_mcs)
val_ds2 = ConcatLblDataset(md.val_ds, val_mcs)
md.trn_dl.dataset = trn_ds2
md.val_dl.dataset = val_ds2
Setup some plotting functions
import matplotlib.cm as cmx
import matplotlib.colors as mcolors
from cycler import cycler
def get_cmap(N):
color_norm = mcolors.Normalize(vmin=0, vmax=N-1)
return cmx.ScalarMappable(norm=color_norm, cmap='Set3').to_rgba
def show_ground_truth(ax, im, bbox, clas=None, prs=None, thresh=0.3):
bb = [bb_hw(o) for o in bbox.reshape(-1,4)]
if prs is None: prs = [None]*len(bb)
if clas is None: clas = [None]*len(bb)
ax = show_img(im, ax=ax)
for i,(b,c,pr) in enumerate(zip(bb, clas, prs)):
if((b[2]>0) and (pr is None or pr > thresh)):
draw_rect(ax, b, color=colr_list[i%num_colr])
txt = f'{i}: '
if c is not None: txt += ('bg' if c==len(id2cat) else id2cat[c])
if pr is not None: txt += f' {pr:.2f}'
draw_text(ax, b[:2], txt, color=colr_list[i%num_colr])
num_colr = 12
cmap = get_cmap(num_colr)
colr_list = [cmap(float(x)) for x in range(num_colr)]
View the Sample labels
x,y=to_np(next(iter(md.val_dl)))
x=md.val_ds.ds.denorm(x)
x,y=to_np(next(iter(md.trn_dl)))
x=md.trn_ds.ds.denorm(x)
fig, axes = plt.subplots(3, 4, figsize=(16, 12))
for i,ax in enumerate(axes.flat):
show_ground_truth(ax, x[i], y[0][i], y[1][i])
plt.tight_layout()
Make a model to predict what shows up in a 4x4 grid
-
anc_grid= how big of a square grid to make (subdivision) -
anc_offset= center offsets -
anc_x= x coordinates for centers -
anc_y= y coordinates for centers -
anc_ctrs- the actual coordinates for the grid centers -
anc_sizes- size of the quadrants
anc_grid = 4
k = 1
anc_offset = 1/(anc_grid*2)
anc_x = np.repeat(np.linspace(anc_offset, 1-anc_offset, anc_grid), anc_grid)
anc_y = np.tile(np.linspace(anc_offset, 1-anc_offset, anc_grid), anc_grid)
anc_ctrs = np.tile(np.stack([anc_x,anc_y], axis=1), (k,1))
anc_sizes = np.array([[1/anc_grid,1/anc_grid] for i in range(anc_grid*anc_grid)])
anchors = V(np.concatenate([anc_ctrs, anc_sizes], axis=1), requires_grad=False).float()
grid_sizes = V(np.array([1/anc_grid]), requires_grad=False).unsqueeze(1)
anchors
Variable containing:
0.1250 0.1250 0.2500 0.2500
0.1250 0.3750 0.2500 0.2500
0.1250 0.6250 0.2500 0.2500
0.1250 0.8750 0.2500 0.2500
0.3750 0.1250 0.2500 0.2500
0.3750 0.3750 0.2500 0.2500
0.3750 0.6250 0.2500 0.2500
0.3750 0.8750 0.2500 0.2500
0.6250 0.1250 0.2500 0.2500
0.6250 0.3750 0.2500 0.2500
0.6250 0.6250 0.2500 0.2500
0.6250 0.8750 0.2500 0.2500
0.8750 0.1250 0.2500 0.2500
0.8750 0.3750 0.2500 0.2500
0.8750 0.6250 0.2500 0.2500
0.8750 0.8750 0.2500 0.2500
[torch.cuda.FloatTensor of size 16x4 (GPU 0)]
plt.scatter(anc_x, anc_y)
plt.xlim(0, 1)
plt.ylim(0, 1);
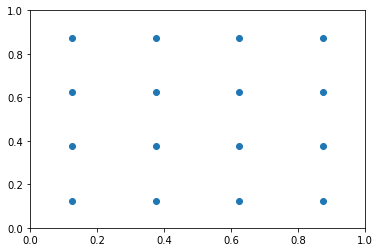
#anchors = anchors.cpu(); grid_sizes = grid_sizes.cpu(); anchor_cnr = anchor_cnr.cpu()
def hw2corners(ctr, hw): return torch.cat([ctr-hw/2, ctr+hw/2], dim=1)
anchor_cnr = hw2corners(anchors[:,:2], anchors[:,2:])
anchor_cnr
Variable containing:
0.0000 0.0000 0.2500 0.2500
0.0000 0.2500 0.2500 0.5000
0.0000 0.5000 0.2500 0.7500
0.0000 0.7500 0.2500 1.0000
0.2500 0.0000 0.5000 0.2500
0.2500 0.2500 0.5000 0.5000
0.2500 0.5000 0.5000 0.7500
0.2500 0.7500 0.5000 1.0000
0.5000 0.0000 0.7500 0.2500
0.5000 0.2500 0.7500 0.5000
0.5000 0.5000 0.7500 0.7500
0.5000 0.7500 0.7500 1.0000
0.7500 0.0000 1.0000 0.2500
0.7500 0.2500 1.0000 0.5000
0.7500 0.5000 1.0000 0.7500
0.7500 0.7500 1.0000 1.0000
[torch.cuda.FloatTensor of size 16x4 (GPU 0)]
n_clas = len(id2cat)+1
n_act = k*(4+n_clas)
This is a simple Conv Model
class StdConv(nn.Module):
def __init__(self, nin, nout, stride=2, drop=0.1):
super().__init__()
self.conv = nn.Conv2d(nin, nout, 3, stride=stride, padding=1)
self.bn = nn.BatchNorm2d(nout)
self.drop = nn.Dropout(drop)
def forward(self, x): return self.drop(self.bn(F.relu(self.conv(x))))
def flatten_conv(x,k):
bs,nf,gx,gy = x.size()
x = x.permute(0,2,3,1).contiguous()
return x.view(bs,-1,nf//k)
This is an output Conv Model with 2 Conv2d layers
class OutConv(nn.Module):
def __init__(self, k, nin, bias):
super().__init__()
self.k = k
self.oconv1 = nn.Conv2d(nin, (len(id2cat)+1)*k, 3, padding=1)
self.oconv2 = nn.Conv2d(nin, 4*k, 3, padding=1)
self.oconv1.bias.data.zero_().add_(bias)
def forward(self, x):
return [flatten_conv(self.oconv1(x), self.k),
flatten_conv(self.oconv2(x), self.k)]
The SSD Model
-
Stride 1 Convolution- doesn’t change the dimension size, but we have a mini neural network -
StdConv- a combination block ofConv2d,BatchNorm,Dropoutdefined above. -
OutConv- a combination block ofConv2d, 4 x Stride 1,Conv2d, C x Stride 1with two layers we are outputting4 + C
Note that we are adding one more class for background.
class SSD_Head(nn.Module):
def __init__(self, k, bias):
super().__init__()
self.drop = nn.Dropout(0.25)
self.sconv0 = StdConv(512,256, stride=1)
# self.sconv1 = StdConv(256,256)
self.sconv2 = StdConv(256,256)
self.out = OutConv(k, 256, bias)
def forward(self, x):
x = self.drop(F.relu(x))
x = self.sconv0(x)
# x = self.sconv1(x)
x = self.sconv2(x)
return self.out(x)
head_reg4 = SSD_Head(k, -3.)
models = ConvnetBuilder(f_model, 0, 0, 0, custom_head=head_reg4)
learn = ConvLearner(md, models)
learn.opt_fn = optim.Adam
k
1
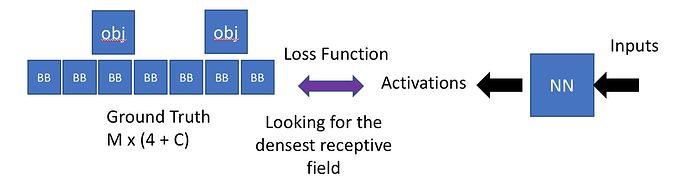
How do we write a loss function for this?
- Has to look at each of these 16 sets of activations, which will each have 4 bounding box and categories + 1
- The loss function actually needs to take each object in the image and match them to a convolutional grid cell. This is called the matching problem
def one_hot_embedding(labels, num_classes):
return torch.eye(num_classes)[labels.data.cpu()]
class BCE_Loss(nn.Module):
def __init__(self, num_classes):
super().__init__()
self.num_classes = num_classes
def forward(self, pred, targ):
t = one_hot_embedding(targ, self.num_classes+1)
t = V(t[:,:-1].contiguous())#.cpu()
x = pred[:,:-1]
w = self.get_weight(x,t)
return F.binary_cross_entropy_with_logits(x, t, w, size_average=False)/self.num_classes
def get_weight(self,x,t): return None
loss_f = BCE_Loss(len(id2cat))
Reminder - 4x4 quadrants there’s 20 classes, 1 background + 4 channels
fn bbox
0 000012.jpg 96 155 269 350
1 000017.jpg 61 184 198 278 77 89 335 402
Feeds a high number if it IS a good reflection, and a low number is lower.
def intersect(box_a, box_b):
""" Returns the intersection of two boxes """
max_xy = torch.min(box_a[:, None, 2:], box_b[None, :, 2:])
min_xy = torch.max(box_a[:, None, :2], box_b[None, :, :2])
inter = torch.clamp((max_xy - min_xy), min=0)
return inter[:, :, 0] * inter[:, :, 1]
def box_sz(b):
""" Returns the box size"""
return ((b[:, 2]-b[:, 0]) * (b[:, 3]-b[:, 1]))
def jaccard(box_a, box_b):
""" Returns the jaccard distance between two boxes"""
inter = intersect(box_a, box_b)
union = box_sz(box_a).unsqueeze(1) + box_sz(box_b).unsqueeze(0) - inter
return inter / union
def get_y(bbox,clas):
""" ??? """
bbox = bbox.view(-1,4)/sz
bb_keep = ((bbox[:,2]-bbox[:,0])>0).nonzero()[:,0]
return bbox[bb_keep],clas[bb_keep]
def actn_to_bb(actn, anchors):
""" activations to bounding boxes """
actn_bbs = torch.tanh(actn)
actn_centers = (actn_bbs[:,:2]/2 * grid_sizes) + anchors[:,:2]
actn_hw = (actn_bbs[:,2:]/2+1) * anchors[:,2:]
return hw2corners(actn_centers, actn_hw)
def map_to_ground_truth(overlaps, print_it=False):
""" ?? """
prior_overlap, prior_idx = overlaps.max(1)
if print_it: print(prior_overlap)
# pdb.set_trace()
gt_overlap, gt_idx = overlaps.max(0)
gt_overlap[prior_idx] = 1.99
for i,o in enumerate(prior_idx): gt_idx[o] = i
return gt_overlap,gt_idx
def ssd_1_loss(b_c,b_bb,bbox,clas,print_it=False):
bbox,clas = get_y(bbox,clas)
a_ic = actn_to_bb(b_bb, anchors)
overlaps = jaccard(bbox.data, anchor_cnr.data)
gt_overlap,gt_idx = map_to_ground_truth(overlaps,print_it)
gt_clas = clas[gt_idx]
pos = gt_overlap > 0.4
pos_idx = torch.nonzero(pos)[:,0]
gt_clas[1-pos] = len(id2cat)
gt_bbox = bbox[gt_idx]
loc_loss = ((a_ic[pos_idx] - gt_bbox[pos_idx]).abs()).mean()
clas_loss = loss_f(b_c, gt_clas)
return loc_loss, clas_loss
def ssd_loss(pred,targ,print_it=False):
lcs,lls = 0.,0.
for b_c,b_bb,bbox,clas in zip(*pred,*targ):
loc_loss,clas_loss = ssd_1_loss(b_c,b_bb,bbox,clas,print_it)
lls += loc_loss
lcs += clas_loss
if print_it: print(f'loc: {lls.data[0]}, clas: {lcs.data[0]}')
return lls+lcs
Test to make sure that model works
x,y = next(iter(md.val_dl))
#x,y = V(x).cpu(),V(y)
x,y = V(x),V(y)
learn.model.cuda()
batch = learn.model(x)
#ssd_loss(batch, y, True)
learn.model.cuda()
batch = learn.model(x)
type(batch[0].data), type(y[0].data)
(torch.cuda.FloatTensor, torch.cuda.FloatTensor)
Train the model
learn.crit = ssd_loss
lr = 3e-3
lrs = np.array([lr/100,lr/10,lr])
learn.lr_find(lrs/1000,1.)
learn.sched.plot(1)
learn.fit(lr, 1, cycle_len=1, use_clr=(20,3))
learn.fit(lr, 1, cycle_len=5, use_clr=(20,10))
learn.save('0')
epoch trn_loss val_loss
0 178.904678 179954.0
epoch trn_loss val_loss
0 41.900517 30.778248
epoch trn_loss val_loss
0 31.734285 29.830471
1 29.553838 28.571745
2 27.744743 26.556757
3 26.028599 26.084572
4 24.452854 25.413759
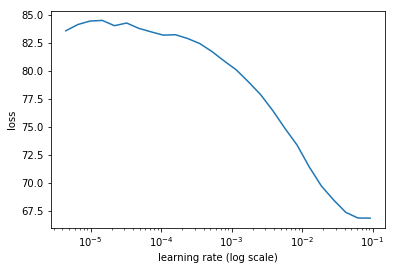
learn.load('0')
Let’s walk through a Loss Function
# grab a single batch
x,y = next(iter(md.val_dl))
# turn into variables
x,y = V(x),V(y)
# set model to eval mode (trained in the previous block)
learn.model.eval()
batch = learn.model(x)
# destructure the class and the bounding box
b_clas,b_bb = batch
The dimensions
- 64 Batch size by
- 16 Grid cells
- 21 classes
- 4 Bounding Box coord
b_clas.size(),b_bb.size()
(torch.Size([64, 16, 21]), torch.Size([64, 16, 4]))
Looking at image 7
idx=7
# class
b_clasi = b_clas[idx]
# bounding box
b_bboxi = b_bb[idx]
# image
ima=md.val_ds.ds.denorm(to_np(x))[idx]
# bounding box / classification
bbox,clas = get_y(y[0][idx], y[1][idx])
bbox,clas
(Variable containing:
0.6786 0.4866 0.9911 0.6250
0.7098 0.0848 0.9911 0.5491
0.5134 0.8304 0.6696 0.9063
[torch.cuda.FloatTensor of size 3x4 (GPU 0)], Variable containing:
8
10
17
[torch.cuda.LongTensor of size 3 (GPU 0)])
Truth of Image 7
# Convert torch tensors to numpy
def torch_gt(ax, ima, bbox, clas, prs=None, thresh=0.4):
return show_ground_truth(ax, ima, to_np((bbox*224).long()),
to_np(clas), to_np(prs) if prs is not None else None, thresh)
fig, ax = plt.subplots(figsize=(7,7))
torch_gt(ax, ima, bbox, clas)

Look at our 16 anchor boxes
fig, ax = plt.subplots(figsize=(7,7))
torch_gt(ax, ima, anchor_cnr, b_clasi.max(1)[1])

Let’s look at the sofa
Lets look at the area of intersection with boxes 7 and 11

The Jaccard index will be the area of intersection over the area over union. In this picture it is the green area over green + yellow. Higher jaccard index = higher intersection
For Every object ( 0 Chair, 1 Dining, 2 Sofa) we will compare and calc Jaccard index, result is 3x16 matrix
Lets first look at the anchor coordinates. center x | center y | height | width
anchors
Variable containing:
0.1250 0.1250 0.2500 0.2500
0.1250 0.3750 0.2500 0.2500
0.1250 0.6250 0.2500 0.2500
0.1250 0.8750 0.2500 0.2500
0.3750 0.1250 0.2500 0.2500
0.3750 0.3750 0.2500 0.2500
0.3750 0.6250 0.2500 0.2500
0.3750 0.8750 0.2500 0.2500
0.6250 0.1250 0.2500 0.2500
0.6250 0.3750 0.2500 0.2500
0.6250 0.6250 0.2500 0.2500
0.6250 0.8750 0.2500 0.2500
0.8750 0.1250 0.2500 0.2500
0.8750 0.3750 0.2500 0.2500
0.8750 0.6250 0.2500 0.2500
0.8750 0.8750 0.2500 0.2500
[torch.cuda.FloatTensor of size 16x4 (GPU 0)]
Get the activtions
a_ic = actn_to_bb(b_bboxi, anchors)
fig, ax = plt.subplots(figsize=(7,7))
torch_gt(ax, ima, a_ic, b_clasi.max(1)[1], b_clasi.max(1)[0].sigmoid(), thresh=0.0)
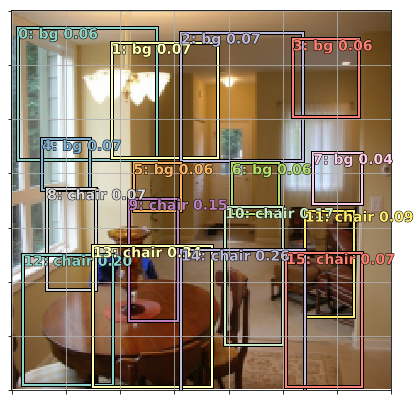
Calculate Jaccard index (all objects x all grid cells)
overlaps = jaccard(bbox.data, anchor_cnr.data)
overlaps
Columns 0 to 9
0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0091
0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0356 0.0549
0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
Columns 10 to 15
0.0922 0.0000 0.0000 0.0315 0.3985 0.0000
0.0103 0.0000 0.2598 0.4538 0.0653 0.0000
0.0000 0.1897 0.0000 0.0000 0.0000 0.0000
[torch.cuda.FloatTensor of size 3x16 (GPU 0)]
For each object, we can find the highest overlap with any cell
Returns:
- Maximum amount
- And the corresponding cell index
# Dining Table
overlaps.max(1)
(
0.3985
0.4538
0.1897
[torch.cuda.FloatTensor of size 3 (GPU 0)],
14
13
11
[torch.cuda.LongTensor of size 3 (GPU 0)])
# Chair
overlaps.max(0)
(
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0356
0.0549
0.0922
0.1897
0.2598
0.4538
0.3985
0.0000
[torch.cuda.FloatTensor of size 16 (GPU 0)],
0
0
0
0
0
0
0
0
1
1
0
2
1
1
0
0
[torch.cuda.LongTensor of size 16 (GPU 0)])
Combine overlaps with map_to_ground_truth
- Object gets assigned to a cell if it has maximum value
- Remaining cells get assigned to objects that have 0.5 or more
- All others are considered backgrounds
gt_overlap,gt_idx = map_to_ground_truth(overlaps)
gt_overlap,gt_idx
(
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0356
0.0549
0.0922
1.9900
0.2598
1.9900
1.9900
0.0000
[torch.cuda.FloatTensor of size 16 (GPU 0)],
0
0
0
0
0
0
0
0
1
1
0
2
1
1
0
0
[torch.cuda.LongTensor of size 16 (GPU 0)])
Convert to Classes
gt_clas = clas[gt_idx]; gt_clas
Variable containing:
8
8
8
8
8
8
8
8
10
10
8
17
10
10
8
8
[torch.cuda.LongTensor of size 16 (GPU 0)]
Comparing Ground Truth Objects to fixed anchor boxes.
thresh = 0.5
pos = gt_overlap > thresh
pos_idx = torch.nonzero(pos)[:,0]
neg_idx = torch.nonzero(1-pos)[:,0]
pos_idx
11
13
14
[torch.cuda.LongTensor of size 3 (GPU 0)]
Show the Cell Assignment
gt_clas[1-pos] = len(id2cat)
[id2cat[o] if o<len(id2cat) else 'bg' for o in gt_clas.data]
['bg',
'bg',
'bg',
'bg',
'bg',
'bg',
'bg',
'bg',
'bg',
'bg',
'bg',
'sofa',
'bg',
'diningtable',
'chair',
'bg']
End the Matching Stage
loc_loss = L1_loss = mean(|matched_activations - ground truth|)
gt_bbox = bbox[gt_idx]
loc_loss = ((a_ic[pos_idx] - gt_bbox[pos_idx]).abs()).mean()
clas_loss = F.cross_entropy(b_clasi, gt_clas)
loc_loss,clas_loss
(Variable containing:
1.00000e-02 *
5.8389
[torch.cuda.FloatTensor of size 1 (GPU 0)], Variable containing:
0.8217
[torch.cuda.FloatTensor of size 1 (GPU 0)])
Let’s plot a few pictures
fig, axes = plt.subplots(3, 4, figsize=(16, 12))
for idx,ax in enumerate(axes.flat):
ima=md.val_ds.ds.denorm(to_np(x))[idx]
bbox,clas = get_y(y[0][idx], y[1][idx])
ima=md.val_ds.ds.denorm(to_np(x))[idx]
bbox,clas = get_y(bbox,clas); bbox,clas
a_ic = actn_to_bb(b_bb[idx], anchors)
torch_gt(ax, ima, a_ic, b_clas[idx].max(1)[1], b_clas[idx].max(1)[0].sigmoid(), 0.01)
plt.tight_layout()
Clipping input data to the valid range for imshow with RGB data ([0..1] for floats or [0..255] for integers).
How do we interpret Activations?
Each predicted bounding box, can be moved up to 50%, twice or half as large. We have to convert the activations into a scaling.
def actn_to_bb(actn, anchors):
""" activations to bounding boxes """
actn_bbs = torch.tanh(actn)
actn_centers = (actn_bbs[:,:2]/2 * grid_sizes) + anchors[:,:2]
actn_hw = (actn_bbs[:,2:]/2+1) * anchors[:,2:]
return hw2corners(actn_centers, actn_hw)
Each box can only have one object associated with it. Its possible for an anchorbox to have NOTHING in it. We could:
- treat background as a class - difficult, because its asking the NN to say ‘does this square NOT have 20 other things’
- BCE loss, checks by process of elimination - if there’s no 20 objecst detected, then its background (0 positives)
def one_hot_embedding(labels, num_classes):
return torch.eye(num_classes)[labels.data.cpu()]
class BCE_Loss(nn.Module):
def __init__(self, num_classes):
super().__init__()
self.num_classes = num_classes
def forward(self, pred, targ):
t = one_hot_embedding(targ, self.num_classes+1)
t = V(t[:,:-1].contiguous())#.cpu()
x = pred[:,:-1]
w = self.get_weight(x,t)
return F.binary_cross_entropy_with_logits(x, t, w, size_average=False)/self.num_classes
def get_weight(self,x,t): return None
loss_f = BCE_Loss(len(id2cat))
SSD Loss
# total SSD loss for batch
def ssd_loss(pred,targ,print_it=False):
lcs,lls = 0.,0.
for b_c,b_bb,bbox,clas in zip(*pred,*targ):
loc_loss,clas_loss = ssd_1_loss(b_c,b_bb,bbox,clas,print_it)
lls += loc_loss
lcs += clas_loss
if print_it: print(f'loc: {lls.data[0]}, clas: {lcs.data[0]}')
return lls+lcs
# SSD loss for one image
def ssd_1_loss(b_c,b_bb,bbox,clas,print_it=False):
# get bounding box and classes
bbox,clas = get_y(bbox,clas)
# activations to bounding box
a_ic = actn_to_bb(b_bb, anchors)
# calculate overlaps
overlaps = jaccard(bbox.data, anchor_cnr.data)
# get the overlaps based on the criteria
gt_overlap,gt_idx = map_to_ground_truth(overlaps,print_it)
# get the classes
gt_clas = clas[gt_idx]
# find the positives
pos = gt_overlap > 0.4
pos_idx = torch.nonzero(pos)[:,0]
# do the cell assignments
gt_clas[1-pos] = len(id2cat)
gt_bbox = bbox[gt_idx]
# calc L1 loss and cross entropy loss
loc_loss = ((a_ic[pos_idx] - gt_bbox[pos_idx]).abs()).mean()
clas_loss = loss_f(b_c, gt_clas)
return loc_loss, clas_loss
How can we improve?
Let’s increase the resolution of the anchor boxes.
Create Anchor Boxes of different sizes / Aspect Ratios ( 3 aspect ratios, 3 zooms)
Use more conv. layers as source of anchor boxes
4 x 4 , 2 x 2, 1 x 1
We can combine the methods to create a LOT of anchor boxes
# Grid cell sizes
anc_grids = [4,2,1]
anc_zooms = [0.75, 1., 1.3]
anc_ratios = [(1.,1.), (1.,0.5), (0.5,1.)]
anchor_scales = [(anz*i,anz*j) for anz in anc_zooms for (i,j) in anc_ratios]
k = len(anchor_scales)
anc_offsets = [1/(o*2) for o in anc_grids]
k
9
Make the Corners
anc_x = np.concatenate([np.repeat(np.linspace(ao, 1-ao, ag), ag)
for ao,ag in zip(anc_offsets,anc_grids)])
anc_y = np.concatenate([np.tile(np.linspace(ao, 1-ao, ag), ag)
for ao,ag in zip(anc_offsets,anc_grids)])
anc_ctrs = np.repeat(np.stack([anc_x,anc_y], axis=1), k, axis=0)
Make the Dimensions
anc_sizes = np.concatenate([np.array([[o/ag,p/ag] for i in range(ag*ag) for o,p in anchor_scales])
for ag in anc_grids])
grid_sizes = V(np.concatenate([np.array([ 1/ag for i in range(ag*ag) for o,p in anchor_scales])
for ag in anc_grids]), requires_grad=False).unsqueeze(1)
anchors = V(np.concatenate([anc_ctrs, anc_sizes], axis=1), requires_grad=False).float()
anchor_cnr = hw2corners(anchors[:,:2], anchors[:,2:])
Change our Architecture, so it spits out enough activations, Sample of Ground Truth
Try to make the activations who closely represents the bounding box
- Now we can have multiple anchor boxes per grid cell
- For every object, have to figure out which anchor box which is closer
- For each anchor box, we have to find which object its responsible for
- We don’t need to necessarily change the number of Conv. Filters. We will get these for free
For ground truth boxes = n x (4 + c)
here’s the Model
-
k= number of zooms x number of aspect ratios. Grids will be for free -
Note the number of
OutConvthere’s many more outputs this time around
class SSD_MultiHead(nn.Module):
def __init__(self, k, bias, drop=0.1):
super().__init__()
self.drop = nn.Dropout(drop)
self.sconv1 = StdConv(512,256, drop=drop)
self.sconv2 = StdConv(256,256, drop=drop)
self.sconv3 = StdConv(256,256, drop=drop)
self.out0 = OutConv(k, 256, bias)
self.out1 = OutConv(k, 256, bias)
self.out2 = OutConv(k, 256, bias)
self.out3 = OutConv(k, 256, bias)
def forward(self, x):
x = self.drop(F.relu(x))
x = self.sconv1(x)
o1c,o1l = self.out1(x)
x = self.sconv2(x)
o2c,o2l = self.out2(x)
x = self.sconv3(x)
o3c,o3l = self.out3(x)
return [torch.cat([o1c,o2c,o3c], dim=1),
torch.cat([o1l,o2l,o3l], dim=1)]
head_reg4 = SSD_MultiHead(k, -4.)
models = ConvnetBuilder(f_model, 0, 0, 0, custom_head=head_reg4)
learn = ConvLearner(md, models)
learn.opt_fn = optim.Adam
learn.crit = ssd_loss
lr = 1e-2
lrs = np.array([lr/100,lr/10,lr])
learn.lr_find(lrs/1000,1.)
learn.sched.plot(n_skip_end=2)
epoch trn_loss val_loss
0 436.807953 900833.375
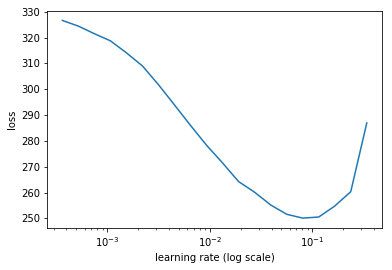
learn.fit(lrs, 1, cycle_len=4, use_clr=(20,8))
epoch trn_loss val_loss
0 153.950207 126.174835
1 119.084206 96.903702
2 99.650275 86.885757
3 86.064523 81.786957
[81.78696]
learn.save('tmp')
learn.freeze_to(-2)
learn.fit(lrs/2, 1, cycle_len=4, use_clr=(20,8))
epoch trn_loss val_loss
0 81.888921 154.412491
1 77.393581 86.504921
2 69.236292 77.665382
3 61.646758 74.613998
[74.614]
Lets look at a batch with probability 0.1
x,y = next(iter(md.val_dl))
y = V(y)
batch = learn.model(V(x))
b_clas,b_bb = batch
x = to_np(x)
fig, axes = plt.subplots(3, 4, figsize=(16, 12))
for idx,ax in enumerate(axes.flat):
ima=md.val_ds.ds.denorm(x)[idx]
bbox,clas = get_y(y[0][idx], y[1][idx])
a_ic = actn_to_bb(b_bb[idx], anchors)
torch_gt(ax, ima, a_ic, b_clas[idx].max(1)[1], b_clas[idx].max(1)[0].sigmoid(), 0.2)
plt.tight_layout()
Clipping input data to the valid range for imshow with RGB data ([0..1] for floats or [0..255] for integers).
Rich History of Object Detection
- 2013 - Multibox method paper. You can have a loss function with a matching process
- Ross Girshick - one conv net makes region proposals, one conv net, fed each region into a separate classifier FAST RCNN
- YOLO & SSD - multibox, but cut through the clutter
- 2017 - FOCAL LOSS RetinaNet - the messy crap doesn’t work.
Where’s the bike!?

If you have a 1 x 1, there’s a good chance you will find an image. If you have a 4 x 4 search, there’s a reduced chance that an object.
Why overlapping + large numbers of anchor boxes?
The jacarrad index calculation makes it difficult to achieve over 0.5 without different sized boxes.
Consider reading the paper.
Paper
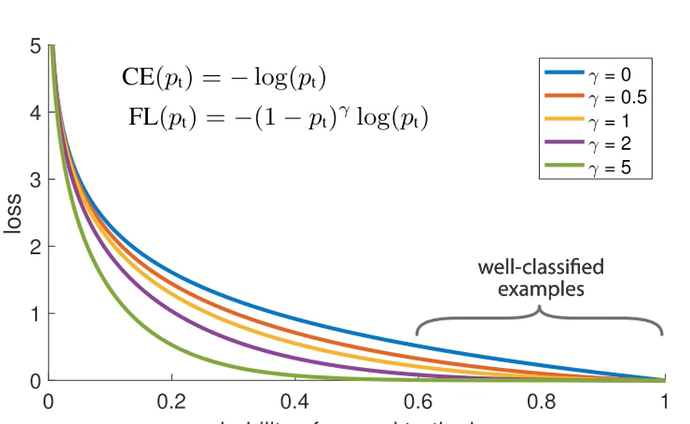
Considering the blue line, even if we are at 0.6 confident, the loss is still pretty high. You can’t simply say its “not background” you have to be confident its one of the 20 classes. So for smaller objects, its not confident enough. Thats also why the boxes are so big for some objects.
So they suggest a new loss function - purple line. The FL function is a scaling function of cross entropy loss
It is amazing that the solution is very elegant, and very straightforward in execution.
How to deal with Class imbalance
Then they define Focal Loss with Class weighting
Focal Loss
def plot_results(thresh):
x,y = next(iter(md.val_dl))
y = V(y)
batch = learn.model(V(x))
b_clas,b_bb = batch
x = to_np(x)
fig, axes = plt.subplots(3, 4, figsize=(16, 12))
for idx,ax in enumerate(axes.flat):
ima=md.val_ds.ds.denorm(x)[idx]
bbox,clas = get_y(y[0][idx], y[1][idx])
a_ic = actn_to_bb(b_bb[idx], anchors)
clas_pr, clas_ids = b_clas[idx].max(1)
clas_pr = clas_pr.sigmoid()
torch_gt(ax, ima, a_ic, clas_ids, clas_pr, clas_pr.max().data[0]*thresh)
plt.tight_layout()
class FocalLoss(BCE_Loss):
def get_weight(self,x,t):
alpha,gamma = 0.25,2.
p = x.sigmoid()
pt = p*t + (1-p)*(1-t)
w = alpha*t + (1-alpha)*(1-t)
return w * (1-pt).pow(gamma)
loss_f = FocalLoss(len(id2cat))
Retrain the model
learn.lr_find(lrs/1000,1.)
learn.sched.plot(n_skip_end=2)
91%|█████████ | 29/32 [00:18<00:01, 1.53it/s, loss=53.9]
learn.fit(lrs, 1, cycle_len=10, use_clr=(20,10))
0%| | 0/32 [00:00<?, ?it/s]
Exception in thread Thread-57:
Traceback (most recent call last):
File "/home/paperspace/anaconda3/envs/fastai/lib/python3.6/threading.py", line 916, in _bootstrap_inner
self.run()
File "/home/paperspace/anaconda3/envs/fastai/lib/python3.6/site-packages/tqdm/_tqdm.py", line 144, in run
for instance in self.tqdm_cls._instances:
File "/home/paperspace/anaconda3/envs/fastai/lib/python3.6/_weakrefset.py", line 60, in __iter__
for itemref in self.data:
RuntimeError: Set changed size during iteration
epoch trn_loss val_loss
0 14.627009 27.391459
1 17.046875 55.384224
2 15.914187 15.103384
3 14.135144 13.905497
4 12.67438 12.506262
5 11.445519 13.349274
6 10.465744 11.700116
7 9.644463 11.588182
8 8.954488 11.204657
9 8.42627 11.142858
[11.142858]
learn.save('fl0')
learn.load('fl0')
learn.freeze_to(-2)
learn.fit(lrs/4, 1, cycle_len=10, use_clr=(20,10))
epoch trn_loss val_loss
0 7.77895 11.484667
1 7.945573 11.758629
2 7.907224 11.412073
3 7.673045 11.21604
4 7.334933 11.071276
5 7.017753 11.007197
6 6.75496 11.007086
7 6.531224 10.968062
8 6.319731 10.930752
9 6.154025 10.955283
[10.955283]
learn.save('drop4')
learn.load('drop4')
x,y = next(iter(md.val_dl))
x,y = V(x),V(y)
batch = learn.model(x)
#ssd_loss(batch, y, True)
plot_results(0.75)
Clipping input data to the valid range for imshow with RGB data ([0..1] for floats or [0..255] for integers).
Non-Maximum Suppression
- Will review the different boxes and compares if the boxes overlap a lot, and if they predict the same thing, and will eliminate the duplicate with the lower p-value.
















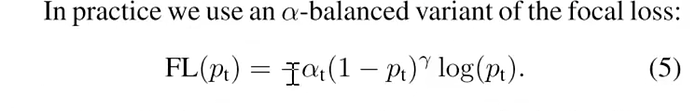

 That’s all the comments I have.
That’s all the comments I have.