Oh no, I just figured I lost my 3 page long draft with the next things I discovered. Hrrr… that “saved” flag on the bottom is very misleading!
I’ll try to reproduce what I did:
I fixed the issue of the hooks by changing the Hook and Hooks inits to allow a name to each hook so I can filter them by name. It was done in the following way:
class Hook():
def __init__(self, m, f, name):
self.hook = m.register_forward_hook(partial(f, self))
self.name = name
class Hooks(ListContainer):
def __init__(self, ms, f): super().__init__([Hook(m, f, m._get_name()) for m in ms])
now I can filter specific modules in my model to show using:
linear_hooks = [h for h in hooks if h.name=='Linear']
relu_hooks = [h for h in hooks if h.name=='ReLU']
and I can then plot the parts that are interesting for me.
I then moved on to initialization. I ranted a bit about how crazy it is that a respected library such as pytorch contains such a basic problem in the initialization of all its layers, that most of the people don’t really know about (I discussed it in depth in one of the replies above). I think its might be preferable for the users not to have initialization at all than having a wrong one implemented.
So with the default pytorch Kaiming_uniform init of the linear layer I get after the usual 70 epochs a score of
train: [0.5789444006975407, tensor(0.7811, device='cuda:0')]
valid: [0.6379683866943181, tensor(0.7638, device='cuda:0')]
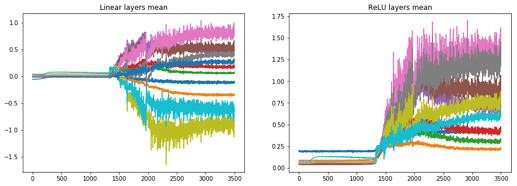
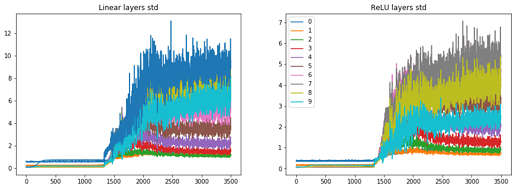
and the stats looks as the following:
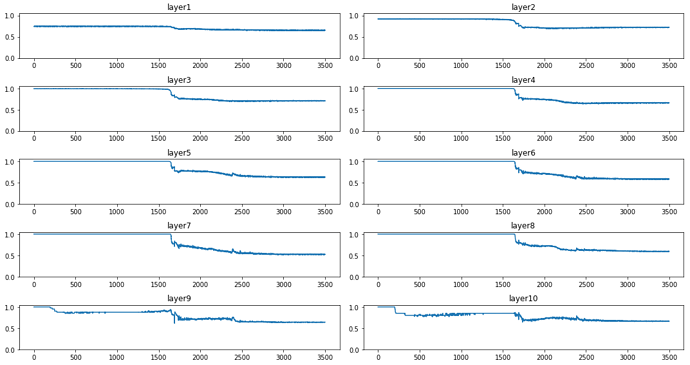
the min-bin graphs are here:
and we can see that mostly in the plateau stage layer 1, 9 and 10 are active and the rest are dormant. When significant learning starts the other layers activations start to grow too.
I’ll try the (hopefully) correct Kaiming initialization, i.e. specifying explicitly the kind of nonlinearity (otherwise it assumes leaky_relu). I chose normal init because its in the actual original Kaiming paper:
for l in model:
if isinstance(l, nn.Sequential):
init.kaiming_normal_(l[0].weight, nonlinearity='relu')
l[0].bias.data.zero_()
I get
train: [0.6051937907277019, tensor(0.7751, device='cuda:0')]
valid: [0.649643508282735, tensor(0.7614, device='cuda:0')]
which seems worse! But as I discovered before, the results have strong variations so maybe I can’t really conclude anything from the end results. What I definitely see is that we still have that long “plateau” period where most of the layers are dormant.
I guess both methods, the “correct” and the wrong one, are not really correct at all.
I could have delved deeper and check whether the layers really have std of 1 along the network depth, but now i feel kind of impatient with the analytical methods (Kaiming, Xavier), and more inclined to try the “All you need is a good init” approach which basically say: forget about trying to analytically calculate the right multiplication factor for each layers weight, and just check what is the std and use its inverse as the multiplier to make sure that the layers’ activation std is 1.
Luckily, @simonjhb wrote a clear post and published a notebook about how to implement this initialization! here is the function from the notebook:
def LSUV(model, tol_var=0.01, t_max=100):
o = x
for m in model:
if hasattr(m,'weight'):
t = 0
u = m(o)
while (u.var() - 1).abs() > tol_var and t < t_max:
t += 1
m.weight.data = m.weight.data/u.std()
u = m(o)
o = u
else:
o = m(o)
return model
Now I really don’t understand why we actually need the loop and iterative process here. Isn’t it correct that when one divides some data by its std one gets std=1 by definition? What am I missing? variation among batches? But anyhow, this function will not update the batch in the inner loop, and after 1 iteration is supposed to have std of exactly 1. Also, what about the non linearity? the activations we want to standardize (std->1) are the ones after the ReLU, because these are the inputs of the next layer, right? I think so, but am not sure. So i’d like to change these 2 things in the LSUV function.
I’m posting so I won’t lose this again and continue in the next post… This feels a bit primitive