Accumulating Gradients

fastai
30

I can create a notebook and share but I am bit busy now. But please feel free to try out yourself.

1 Like
31

I will do…
I will try it on the pet notebook lesson1

1 Like
32

It’s my pleasure contributing and I am happy to be contributing since fast.ai library has such a powerful callback system, very easy to use. Thanks to all devs !

2 Likes
33

By the way currently if you call lr_find it resets to originalOptimWrapper. Don’t know why but investigating. A work around:

def get_learner():
    turn_on_accumulation()
    learn = create_cnn(data=data, arch=models.resnet101,lin_ftrs=[2048], metrics=accuracy,
                       callback_fns=[partial(AccumulateStepper, n_step=25)])
    learn.loss_func = CrossEntropyFlat(reduction="sum")
    return learn

learn = get_learner() 
learn.lr_find() # pick lr
learn = get_learner()
1 Like
34

Here are the notebooks that I am testing now:

github links:
lesson1-pets-v13-grad-accum-OFF-fp32.ipynb https://github.com/hwasiti/fastai-course-v3/blob/master/nbs/dl1/lesson1-pets-v13-grad-accum-OFF-fp32.ipynb
lesson1-pets-v13-grad-accum-ON-fp32.ipynb https://github.com/hwasiti/fastai-course-v3/blob/master/nbs/dl1/lesson1-pets-v13-grad-accum-ON-fp32.ipynb
lesson1-pets-v13-grad-accum-OFF-fp16.ipynb https://github.com/hwasiti/fastai-course-v3/blob/master/nbs/dl1/lesson1-pets-v13-grad-accum-OFF-fp16.ipynb
lesson1-pets-v13-grad-accum-ON-fp16.ipynb https://github.com/hwasiti/fastai-course-v3/blob/master/nbs/dl1/lesson1-pets-v13-grad-accum-ON-fp16.ipynb

I will do a statistical comparison and will report the analysis here shortly.

Please have a look on them and confirm whether they are fine.
Thanks

1 Like
35

Here is the data for running the FP32 notebooks (with or without gradient accumulation):

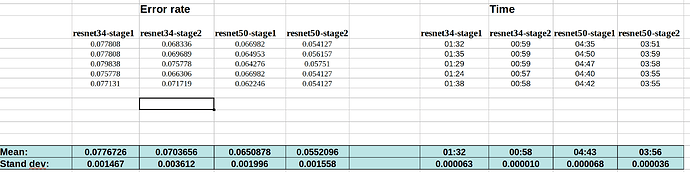
Without grad accum.:

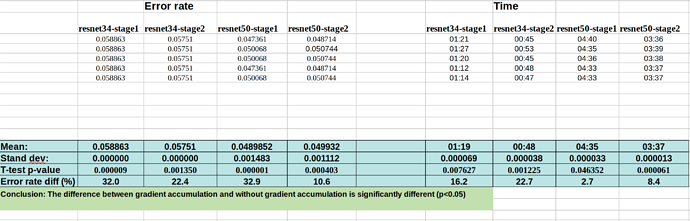
Screenshot%20from%202019-02-19%2014-07-56
Screenshot from 2019-02-19 14-07-56.png2846×912 151 KB

With grad accum.:

Screenshot%20from%202019-02-19%2014-08-12
Screenshot from 2019-02-19 14-08-12.png2788×698 91.8 KB

My intention was to run each notebook 10 times. But from the data, I can see that seed is indeed working perfectly. And there are only tiny variation from run to run within each method.

So the change in the error rate after applying those callbacks is ~25% on average, which cannot be explained by the noise of variation from run to run.

@jeremy
Kerem is going to make a PR request for gradient accumulation with the help of @sgugger . It seems from my analysis above that there is significant difference in the accuracy of doing gradient accumulation of 4 steps with bs=8 (i.e., effectively bs=32), compared to a normal run with bs=32. The difference in error rate is ~25%.
I’ve listed the notebooks used in my previous posts.

Just to be sure before doing the PR, do you think, there is something missing in these callbacks? Isn’t it that we should expect the same error rate in both cases?

1 Like
36

Have you tried fit or fit_one_cycle. Maybe since learning rates will differ during the training, fit_one_cycle might be causing this difference ? Will look closely.

37

I used the same lesson1 notebook without changes. You can have a look on the notebooks in the github links in my previous post.

Any factor (other than what we have introduced, i.e., gradient accumulation) if it has effect from run to run, it would show that variability inside the repetitions of the same group. But we can see from the chart that it is very nicely consistent if we check only the without grad accum. or check only the with grad. accum. group.

38

I see, thanks for the experiments. I will conduct more analysis to see why same effective batch sizes might be giving different results. For example, at very extreme bs=2 n_step=16 bs=32 is far from the same performance of bs=32 without accumulation. Technically this shouldn’t be the case!

I am guessing this might be something to do with the optimizer.

1 Like
39

Here is a Pytorch implementation of gradient accumulation:

1 Like
40

The way I implemented using reduction=sum + params.grad.div()_ works on a Toy example and I am getting the exact same gradient weight updates, both with and without accumulation. The reason we are getting different results by using it as a callback might be a subtle thing which is not related to accumulation but more likely to optimizer.

Here is the toy notebook: https://github.com/KeremTurgutlu/whale/blob/master/Accumulating%20Grad.ipynb

41

I suspect something related to batch normalization. I think it differs for BN if it gets 2 images 16 times than getting 32 images. Maybe BN should be changed to something else like instance normalization or some other BN variant. But this is out of my territory. I hope Jeremy will chime in to help us out…

2 Likes
42

It seems BN is an issue here. If we would PR merge this callback as it is, but getting lower accuracy, I think that would not worth it. Maybe we can find how to remedy this BN issue. But it seems then we have to change the BN layers in the arch?

Most articles did not solve the BN issue when they showed how to do gradient accumulation, and they have not even mentioned it. I think that’s because they haven’t checked whether the accuracy they are getting are the same.

related:

3 Likes
43

Yes, BatchNorm will be problematic and I’m not sure there is a proper workaround.
@kcturgutlu I will try a few changes in the training loop that shouldn’t require the wrapper around the optimizer and allow to skip the step/zero_grad so that it can be all in a Callback

2 Likes
44

Ok, it’s pushed on master. Now, if you return True at the end of on_backward_end, the step is skipped, and if you return True at the end of on_step_end, the zeroing of the gradients is skipped. So if I take your current Callback, both should finish with:

return self.acc_batches % self.n_step == 0
5 Likes
45

Thanks a lot, I will modify the callback with the current changes.

1 Like
46

Being able to control independently and without any hardware restrictions,

  1. Effective batch size for all layers except BN
    AND
  2. Effective batch size for Batch Norm layers

would definitely be useful for many problems.

Most optimal size for 1) and 2) is likely not the same in a lot of problems/datasets.

In this paper they used the concept of ghost batch norm (https://openreview.net/pdf?id=B1Yy1BxCZ) to implement this control. But that is presumably a complex implementation linked to TPU management.

Technically, to solve 2), I guess we need a specific accumulation of BN activations (moving average during forward pass) and syncronized accumulation of gradients before parameters update specific to BN. But, to my understanding, accumulation of BN activations in forward pass in main memory would presumably be very slow and would counter most of the benefit of using the GPU at all.

5 Likes
47

I modified the callback and updated the current PR. Here is a test with a custom head which doesn’t use BN and uses vgg11.

Effective bs = 32 and bs=2 x n_step=16 very similar results.

https://github.com/KeremTurgutlu/whale/blob/master/experimental/Every_nth_Batch_Accumulate_Update%20-%20No%20Batchnorm.ipynb

48

It would be really cool to do accumulation and handle BN layers. What if we create a wrapper over all BN layers at the beginning of training and maybe do forward every n_step while keeping track of desired running_mean and running_var ourselves. Would something like this work?

1 Like
49

Yes, a wrapper around the batchnorm layer would probably best. We might lose speed though, since there might be some optimization in pytorch for this. Might be possible to counter with torch.jit, I’ve just started to experiment with it to do quick custom LSTMs and it seems quite nice.

In any case, we removed all batchnorm in the unet with Jeremy because it was soooo unstable with small batch sizes so I’m pretty sure that it’s the cause of your differences in accumulating grad.

4 Likes