Wiki: Lesson 4

Part 1 (2018)
92

Can someone expline me what every line in the loop does:

print(ss,"\n")
for i in range(50):
    n=res[-1].topk(2)[1]
    n = n[1] if n.data[0]==0 else n[0]
    print(TEXT.vocab.itos[n.data[0]], end=' ')
    res,*_ = m(n[0].unsqueeze(0))
print('...')

When I run it I get the following error:

/home/paperspace/anaconda3/envs/fastai/lib/python3.6/site-packages/ipykernel_launcher.py:5: UserWarning: invalid index of a 0-dim tensor. This will be an error in PyTorch 0.5. Use tensor.item() to convert a 0-dim tensor to a Python number
  """
---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-34-d2cf2df24465> in <module>()
      4     n = n[1] if n.data[0]==0 else n[0]
      5     print(TEXT.vocab.itos[n.data[0]], end=' ')
----> 6     res,*_ = m(n.unsqueeze(0))
      7 print('...')

~/anaconda3/envs/fastai/lib/python3.6/site-packages/torch/nn/modules/module.py in __call__(self, *input, **kwargs)
    489             result = self._slow_forward(*input, **kwargs)
    490         else:
--> 491             result = self.forward(*input, **kwargs)
    492         for hook in self._forward_hooks.values():
    493             hook_result = hook(self, input, result)

~/anaconda3/envs/fastai/lib/python3.6/site-packages/torch/nn/modules/container.py in forward(self, input)
     89     def forward(self, input):
     90         for module in self._modules.values():
---> 91             input = module(input)
     92         return input
     93 

~/anaconda3/envs/fastai/lib/python3.6/site-packages/torch/nn/modules/module.py in __call__(self, *input, **kwargs)
    489             result = self._slow_forward(*input, **kwargs)
    490         else:
--> 491             result = self.forward(*input, **kwargs)
    492         for hook in self._forward_hooks.values():
    493             hook_result = hook(self, input, result)

~/fastai/courses/dl1/fastai/lm_rnn.py in forward(self, input)
     91             dropouth, list of tensors evaluated from each RNN layer using dropouth,
     92         """
---> 93         sl,bs = input.size()
     94         if bs!=self.bs:
     95             self.bs=bs

ValueError: not enough values to unpack (expected 2, got 1)

And I do not really understand the code, therefore I don’t know how to fix it.:neutral_face:

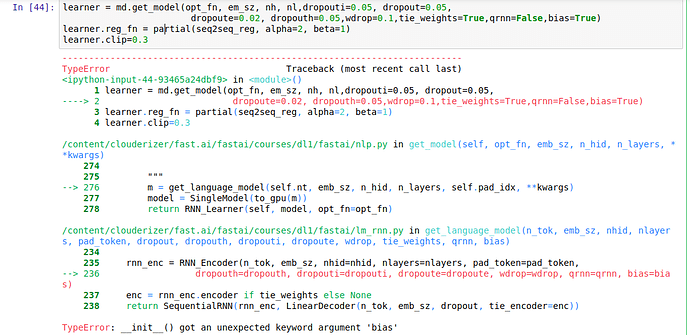
Another problem i have is when running the following code:

m=learner.model
ss=""". So, it wasn't quite was I was expecting, but I really liked it anyway! The best"""
s = [spacy_tok(ss)]
t=TEXT.numericalize(s)
' '.join(s[0])

I get:
TypeError: sequence item 0: expected str instance, spacy.tokens.token.Token found
I believe

1 Like
93

Thanks for the correction!

94

Can anyone explain, why I am getting this error for the following piece of code from Lesson-4

fastai_lesson_4
fastai_lesson_4.png1090×530 82.4 KB

95

The fix for this bug has been merged recently, make a pull of fastai repo.

96

Thanks for the info. After git pull it’s working fine now.

97

Hi all. I have a problem on the predicting structured data part of Lesson 4. I ran the notebook but got different results. My exp_rmspe is so small comparing to what shown in the course. I didn’t change anything. The data I download from the link given in the notebook dataset

new
new.png739×783 61.9 KB

I am very appreciate if someone can help me on this problem. Or can you rerun the notebook to see if you can get the same results or maybe the fastai library change something ?

Thank you

98

Hello,
I’m reading AWD LSTM paper [1708.02182] Regularizing and Optimizing LSTM Language Models
And I cannot understand why in introduction they say

A naïve application of dropout (Srivastava et al., 2014) to an RNN’s hidden state is ineffective as it disrupts the RNN’s ability to retain long term dependencies

What was the state of the art before this article?
And why dropout disrupts RNN?

Update:
As far as I understand, RNN needs to remember the state, and applying dropout ruins state. There is no such problem for not recursive, as every batch has no information that influences next iterations

100

I get the same error:
sequence item 0: expected str instance, spacy.tokens.token.Token found
But I was not able to find a solution here in the forums?
Maybe somebody has a hint?
Is this due to an update of spacy?
Best regards
Michael

101

The notebook has several different ways of defining the validation indices. If you just run the notebook cells in order, you set val_idx=[0] (what you do before training with the entire dataset) before forming your model. If you ran the model with a single validation index, you would be comparing your rmspe to a single value. See what your validation set is, and if it is a single value, try change it to the last two weeks of data via:

val_idx = np.flatnonzero(
    (df.index<=datetime.datetime(2014,9,17)) & (df.index>=datetime.datetime(2014,8,1)))
4 Likes
102

I’m looking for some insight as to how the y_range parameter affects the model and the predictions it makes. Specifically, I’m trying to adapt the methods from the Rossmann example to another structured data problem where the predicted outcome is a binary value - 1, 0.
In the Rossmann notebook, we do the following:

df, y, nas, mapper = proc_df(joined_samp, 'Sales', do_scale=True)
yl = np.log(y)
max_log_y = np.max(yl)
y_range = (0, max_log_y*1.2)
m = md.get_learner(emb_szs, len(df.columns)-len(cat_vars),
               0.04, 1, [1000,500], [0.001,0.01], y_range=y_range)

With sales data, taking the logarithm of sales values works because all sales values are positive numbers. For something where the outcome values range from 0 to 1, taking the log doesn’t really make sense because you get (-inf, 0). Would I just set my y range lower limit to some aribtrary negative number, like y_range=(-100,0)?

Looking a bit deeper, how does y_range affect the prediction outputs of the model? My understanding was .predict() gave the log scale probabilities for a prediction. Is this still the case when output values are constrained by y_range?

1 Like
103

val_idx=[0] is the problem. Thank you a lot. I haven’t read carefully the code but supposing the original code should reproduce the same results. I forget that the original Jupyter notebook code are not run in order.

104

I have latest fast.ai from github and still get
ValueError: not enough values to unpack (expected 2, got 1)
when i run the cell:
print(ss,"\n")
for i in range(50):
n=res[-1].topk(2)[1]
n = n[1] if n.data[0]==0 else n[0]
print(TEXT.vocab.itos[n.data[0]], end=’ ‘)
res = m(n[0].unsqueeze(0))
print(res)
print(’…’)

under Test section. I can’t be the only one.

105

Currently experiencing this error. It looks like the line causing the error is

 res,*_ = m(n[0].unsqueeze(0))

Looking at the stack trace, the issue is in

sl,bs = input.size()
ValueError: not enough values to unpack (expected 2, got 1)

Not really sure what’s going on, but when I run

n[0].unsqueeze(0)

alone, it returns

tensor([ 23], device='cuda:1')

Should it be returning something higher dimensional?

stack
stack.PNG1015×603 36 KB

106

A question about RMSPE. Here’s the formula from Kaggle competition: rmspe
And here’s the implementation from jupyter-notebook:

def exp_rmspe(y_pred, targ):
    targ = inv_y(targ)
    pct_var = (targ - inv_y(y_pred))/targ
    return math.sqrt((pct_var**2).mean())

Shouldn’t we divide by y_pred (y_i on picture) and not by targ (y_hat_i on picture)?
So for me it should look more like this:

def exp_rmspe(y_pred, targ):
    y_pred = inv_y(y_pred)
    targ = inv_y(targ)
    pct_var = (y_pred - targ)/y_pred
    return math.sqrt((pct_var**2).mean())

And all this assuming we get log-values of targ variable while evaluating our metric (couldn’t find this part in source code). Will appreciate any help!

107

Hello everyone, I have a question regarding the embedding of unknown classes. Say if testing data has a new class that has never appeared in training, what will the embedding vector be for the unknown class? Is it randomly assigned?

In my opinion (which could be totally wrong), the most reasonable approach is weights for unknown classes are also trained (anything that is new in valid is considered as unknown), but this probably will involve apply_cats(train, valid) in addition to apply_cats(data, test).

I am asking because I am participating in a competition in detecting frauds, and for many categorial variables, the test data contain new categories. This could possibly mean that new attack methods are deployed in test (the testing data are more recent in time). In this case, the embedding weights of the unknown class could be very important. Any explanation/feedback is greatly appreciated!

1 Like
108

I think you confused notation. targ (our target, actual value) is y_i and y_pred (our prediction) is y_hat?

2 Likes
110

Yes, you’re correct. That’s totally my mistake. Thanks for help!

111

In the rossmann notebook:
y_range = (0, max_log_y*1.2)

If I get it, y_range specifies the range of values for y, and so my question is, how do find y_range for different datasets?

1 Like
112

Hmm, can anybody enlighten me how to write formulas here please?

Thank you very much for the reference! I’ve been breaking my head over this one because Jeremy did not explain this correctly.

So, we want to replace the correct output (y) and our predicted output (\hat{y}) by something so that an existing function (RMSE) of this “something” will be approximately RMSPE of the predicted output relative to correct output. They use the same function f for both the predicted and correct outputs, even though I don’t think they have to (the transformation of y is done offline in advance in any way we want, whereas to get \hat{y} from the output of the neural network, we would need to invert our f). So, the requirement is that f(y) - f(\hat{y}) = \frac{y - \hat{y}}{y}. Again, formally, it’s enough to have equality in absolute value because look at squares of these, but there is no reason not to aim for actual equality.

Now, is there such a function? First, there is no exact solution because, for example, the derivative with respect to y would be proportional to \hat{y}, i.e. f’(y) = \frac{\hat{y}}{y^2}, which does not make sense because f is a function of a single variable. But if we are aiming for \hat{y} to be close to y, we just need approximate equality between our RMSE and the actual RMSPE where \hat{y} \approx y. Then using Taylor’s expansion, we write f({\hat y}) \approx f(y) + f’(y)*(\hat{y} - y). Substituting into f(y) - f(\hat{y}) = \frac{y - \hat{y}}{y}, we get f’(y) \approx \frac{1}{y}. Since y is positive, we conclude that f is approximately the logarithm (plus a constant, which would be immediately eliminated in f(y) - f(\hat{y}), so we set it to zero).

I guess that since we’ve used a few approximations and assumptions along the way, the above is just good intuition for why to try the logarithm. We also need to check that it works well in practice - and apparently it does.

113

Quick question, can we use embeddings to representation a entire database table? I am trying to use some of the methods in this chapter to join two datasets with a one to many relationship? Its a binary classification task and the resulting matrix has duplicate results after joining on the id field as it should? Some ids have 5 records in the joining table while others have 2?