Why ReLU activation cannot fit my toy example - sinus function

cypreess · June 12, 2017, 6:42am

Hi,

to better understand “moving parts” of NN architecture I created a simple toy-problem using sample of sinus function.

I already asked that question here but with no success: https://stats.stackexchange.com/questions/284203/why-relu-activation-cannot-fit-my-toy-example-sinus-function-keras

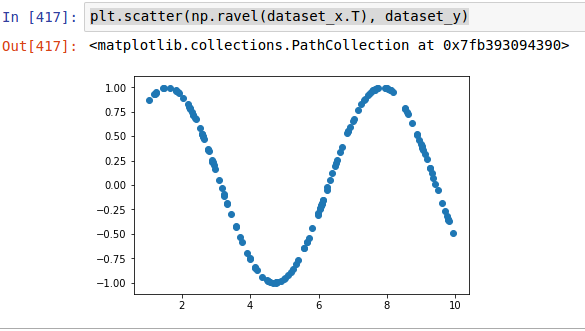
I have a toy example of modeling sinus function using simple FC layer NN. My input data is just 150 data points uniformly randomized in range from 0 to 10.

I started from fiting NN using tanh activation with following architecture:

model = Sequential([
    Dense(10, input_shape=(1,), activation='tanh'), 
    Dense(1),
])
model.fit(dataset_x, dataset_y, batch_size=32, validation_split=0.1, nb_epoch=10000, verbose=0)

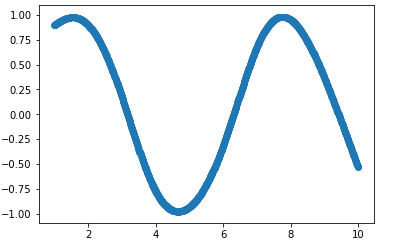
It took 10000 epochs to get fit like this:

tanh activation fit after 10k epochs

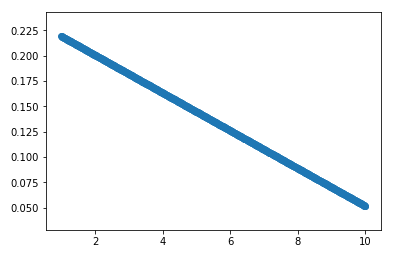
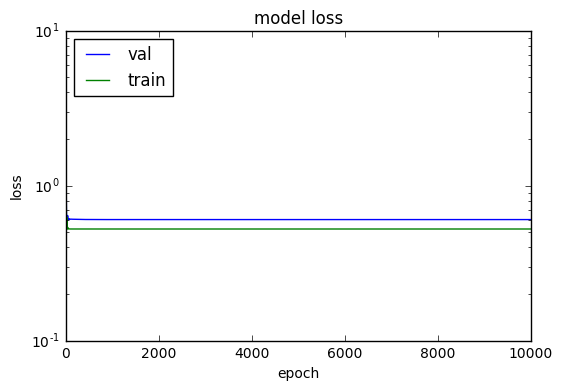
Running the same code but switching only activation from tanh to relu cannot converge at any fit. Not even for 20-30k epochs.

ReLU activation fit after 10k+ epochs

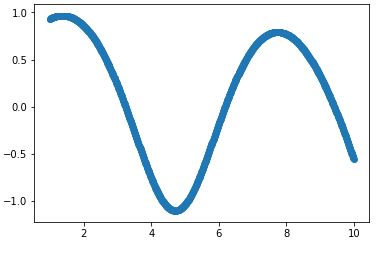
However if I switch to softened ReLU (softplus) it somehow fits but requires at least 2x more epochs to fit anything close to the result using tanh.

Softplus activation fit after 20k epochs

So the general question is why this happens?

Additional questions/thoughts I have are:

Does it have anything in common to the fact that the shape of tanh and softplus functions is curved and ReLU is just two linear functions bound together?
Maybe ReLU requires some different architecture of NN to work here, or maybe using some regularization (I tried some L1, L2 but did not helped) or any other kind of modificiation because it just canot model non-linear functions using this architecrtre I have (I tried adding more hidden layers without luck).

I am really missing here some intuition why this happens, as ReLU is advertised as the best/fastest activation that should be know used by default in any NN.

amanmadaan · June 13, 2017, 3:13am

Can you please share the complete code (data generation, plotting etc.)?

cypreess · June 13, 2017, 9:58pm

Hi Aman,

sure I can. Its here: https://www.dropbox.com/s/xah9awuozvexyeo/sin%20nn.ipynb?dl=0

amanmadaan · June 14, 2017, 7:15pm

##1. Fitting vs. Overfitting

Let’s start by noting that the question here is about the relu being unable to overfit, and not fit. This is because the prediction plots are on the input (training) range (i.e. the model is trained on the inputs between [1, 10], and the predictions are also done on the same interval [1, 10]) . There is nothing to be learned in the features that we supply to any of the models. Sure, we provide the model with the information that output for 5 is tanh(5), but why are we expecting the model to learn anything about tanh(50)?

Here are the predictions from the tanh version for inputs in [40, 50]:

As expected, not very interesting.

2. Relu and the Positivity

So why is it that relu fails to overfit the data?

Let’s recall the definition of relu:

relu(x) = max(x, 0)

In contrast, the output of tanh is between [-1, 1].

This implies that the output of the single layer that we have is just positive numbers. On top of that, we start with only positive numbers in our input [1, 10].

If you write the backprop expressions, you will see that the gradients of the weights of the first layer are always multiplied by the input x. The input, thus introduces no variation in the direction of the gradients.

This saturation implies that there will be no change in the loss, which is the case as we see from the learning plots:

This also explains the monotinically increasing/decreasing predictions with the relu model (based on the W initialization, you should see different kinds of lines as relu predictions).

There is simply not enough non-linearity, and thus the uniteresting weights only act as a linear function of the input.

3. Softplus and Small Gradients

added after a follow up from @cypreess

The gradient of softplus is 1 / (1 + e^-x), which is between 0 and 1.

The gradient of the relu on the other hand is just x (for x > 0).

To quote myself from the para above, "'If you write the backprop expressions, you will see that the gradients of the weights of the first layer are always multiplied by the input x. " This is because the gradient of the relu is just the input x.

In the softplus case, the weights of the first layer will be multiplied with this smaller number (gradient of softplus, 1 / (1 + e^-x)), and thus don’t blow up as much.

Also compare the derivate of tanh in [1, 10] with the derivative of softplus in [1, 10].

As you would guess from the plots, tanh has a much smaller derivative.

Note that relu provides as much non linearity as any other activation when we stack a bunch of them together. Just that in this case, the setup favors the use of tanh.

4. Potential Fixes

If we normalize our input data by using the data between [-10, 10], the model seems to be doing some overfitting:

##5. Overcomplicated Models Overfit

As discussed in the lectures, when the model is more complicated than it needs to be, it leads to overfitting (and we resort to regularization etc.). In this case, we want to overfit, so let’s add more layers and make sure the theory of overfitting works
model = Sequential([ Dense(40, input_shape=(1,), activation=‘relu’), Dense(20, input_shape=(1,), activation=‘relu’), Dense(10, input_shape=(1,), activation=‘relu’), Dense(1), ])

However, it’s still overfitting (predictions over [30, 40] for model trained on [-10, 10] ):

I’ve used 10k epochs for all the variations.

6. Learning Sine

As an alternative toy example that learns the sine function, you can consider creating a model that predicts N + 1^th point of sine wave output given then previous N points.

Here is a gist: https://gist.github.com/madaan/5f45e5c6b5b81484fc94e0e765dc445f

Thanks for sharing the code and the question.

cypreess · June 15, 2017, 7:49am

Thank you Aman for such insightfull answer.

I do not understand than why using softplus which also has only positive output actually works and overfits my example.

Softplus did overfit data (my last example I gave). What is the answer for that?

I am just assuming that it adds nonlinearity to the architecture that without it cannot model non-linear problems, and this is not really that much connected with positivity of function.

amanmadaan · June 15, 2017, 9:40am

@cypreess The gradient of softplus is 1 / (1 + e^-x), which is between 0 and 1.

The gradient of the relu on the other hand is just x (for x > 0).

Frrom my answer, "'If you write the backprop expressions, you will see that the gradients of the weights of the first layer are always multiplied by the input x. " This is because the gradient of the relu is just the input x.

In this case, the weights of the first layer will be multiplied with this smaller number (gradient of softplus, 1 / (1 + e^-x)), and thus don’t blow up as much.

Also compare the derivate of tanh in [1, 10] with the derivative of softplus in [1, 10].

As you would guess from the plots, tanh has a much smaller derivative.

Note that relu provides as much non linearity as any other activation when we stack a bunch of them together. Just that in this case, the setup favors the use of tanh.