I thought the functions are applied right to left so I was expecting it to compute 5+3 first then apply the x to 2 and 8 but the result is different from my expectations:
4×2 5+3
20 32
I thought the functions are applied right to left so I was expecting it to compute 5+3 first then apply the x to 2 and 8 but the result is different from my expectations:
4×2 5+3
20 32
2 5 is a vector. So first you take 2 5 + 3. then you multiple the answer of that by 4.
As @Ezno implies, the binding of 2 and 5 (stranding) is stronger than +'s binding of 5.
However, 4×2,5+3 would give you what you expect.
Thank you both! I was actually trying to understand the result from the the Zark tutorial (ch5 page 1)
Is there a list of all the binding/parsing rules somewhere? The precedence I’m aware of is something like:
")., j, upper-bar, digits)Somewhere in there I guess there’s also dyalog specific stuff like ] and ). And quad-prefix stuff (which I guess might be same as symbol-creation). The first 3 above are a bit hand-wavy since there’s more detailed rules than just glyph precedence, but hopefully it’s still a useful rule-of-thumb.
Hey Jeremy,
For a table of all the binding strengths, you can take a look at: https://docs.dyalog.com/latest/CheatSheet%20-%20Binding%20Strengths.pdf
There are some useful papers and functions exploring this more in the annals of dfns.dyalog.com. See Dyalog APL - Simplified version of Dyalog's binding rules:
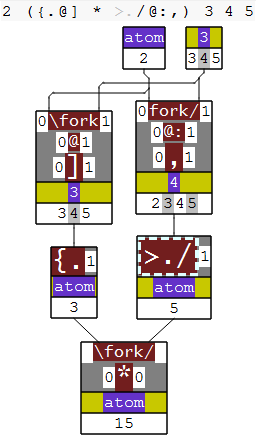
Using the ‘try’ function from that page, we can run Mike’s expression to view the binding tree:
try '4×2 5+3'
A
┌──┴───┐
┌┴┐ ┌─┴─┐
4 × ┌┴─┐ 3
┌┴┐ +
2 5
Of course, this is quite a bit of literature for someone trying to learn the basic language rules, and a short list of the most basic precedence is definitely the way to go when initially teaching APL.
Dyalog specific commands that starts with ] or ) are not part of the language itself, and will not work under program control (i.e. you cannot embed them in a function). You can only run those expressions in the session. Binding rules do not apply to them.
System commands (starting with the right parenthesis) are typically just meant for dealing with the IDE or environment. E.g. running an )OFF to terminate the session. (System command - APL Wiki)
User commands (starting with the right bracket) are typically just utilities that users (including Dyalog) can deploy. These are typically just helpful extensions. E.g. Setting ]box on, or dealing with DevOps features.
The ⎕ prefix stuff you see are simply “System” functions, operators, and variables (constants that you cannot change, or some that you can change) that are useful extensions to bundle with the language. These will work in program control, and fall under the regular binding of a function, operator, or variable.
Here are some various examples of the ⎕prefix items:
⎕A is a “constant” to generate the Alphabet (26 characters, A-Z, in uppercase)
⎕IO is a variable you use to set your Index Origin (One way to compromise on the “Do arrays start at 0 or 1” question ![]() ). Since it’s just a variable, it used to be very common to see people use it in code to write “⎕IO independent code”.
). Since it’s just a variable, it used to be very common to see people use it in code to write “⎕IO independent code”.
Suppose I had a boolean variable b. And I wanted to index a result from it:
'Pass' 'Fail'[⎕IO+b]
Although it may be prettier to just set it somewhere else in your code, and then you don’t need it in your computation. This was just to show that regular APL primitives work as if it was a variable you defined (Obviously setting it IS controlled, you can’t set the index origin to something other than 0 or 1… that would be taking the compromise a little too far!)
⎕NGET is a function that reads from a text file. Since it’s a function, you can apply appropriate operators to it. ⎕NEXISTS is a function as well that returns a boolean telling us if the file does or does not exist. So:
⎕NGET⍣(⎕NEXISTS file)⊢file (Power Boolean is a neat way of conditional execution. Raise my function to the 0th power means do not run it, raising it to the first power means just run it once). Of course, there are better ways to write that line, just showing that you can use regular APL primitive operators on these functions.
Finally, for an operator example: ⎕R and ⎕S are operators that help you perform string searching and replacing, typically using Regular Expressions.
P.S. I’m very excited to see all the discussion and learning that’s going on here. Thank you for your training videos, they are really enjoyable!
Regards,
Josh
The hard part of “getting my eye in” here is that visually a space is a separator rather than a binder
Hi Josh, thanks so much for explaining this and posting the links. I was trying to use the ‘try’ function but I don’t think I know how to activate it. So I tried to run the lines above it (on the page in second link you shared) to see if I could define it myself.
I tried the first line but got the ensuing error:
defns ← scripts._dyalog
VALUE ERROR: Undefined name: scripts
defns←scripts._dyalog
∧
I understand it maybe a bit advanced, but it seems so useful that I wanted to use it with the expressions I’m trying out.
Hi Mike,
So the value error is because ‘try’ is not defined in your workspace yet. When you start off with a clear workspace, you need to load the code in. The )COPY system command will do this, since dfns is a standard workspace distributed with the install. From your session:
)COPY dfns
defns ← scripts._dyalog
try ← defns∘parse
Note, to run the more advanced examples, you should use the “extended binding table”:
xdefs ← scripts._dyalogX
try ← xdefs∘parse ⍝ Handy shortcut.
Josh
Thanks for that explanation Josh! I’m able to run the example now ![]()
Cheers!
Is there any reason not to always use the extended binding table?
Jeremy, that’s a great question which lead me to explore these “try” functions in more detail.
Intuitively, one would think to always run the “extended” binding table. However (to my surprise!), it does not fully encapsulate all the tokens which are in the simpler binding table. “Extended” probably isn’t a good name for it, then. I should’ve been more clear that these functions are very simplified rules of the actual binding tables. They do not include all the tokens one could encounter in a random expression found in the wild. The only surefire way of knowing which table to use, is to look at which tokens are included in each table. Hence, I would only recommend using this function on very simple examples that are included in the tables. For example, only the literal numbers 0-6 are included in both binding tables:
A 0 1 2 3 4 5 6 ⍺ ⍵ a b c d ⍝ * Array
So an expression with 7 in it will not behave properly. I suppose you could replace the 7 in your expression with a number 0-6, or a variable a-d.
Furthermore, there are only a handful of functions included in each binding table. Some functions in the simple definition are not even in the extended one:
Simple table:
F + - × ÷ ⌊ ↓ ⍳ ⍴ ⊂ ≢ , f g ⍝ * Function
Extended table:
F + - × ÷ = ⍳ | ∇ e f g ⍝ * Function
I suppose one could enhance these tables to include more sample tokens. I’ll speak to my colleagues about a possible extension here. At its core, this function uses an implementation of Bunda-Gerth parsing (Dyalog APL - Bunda-Gerth parse of expression ⍵.), which still has some limitations noted on that page under “Bugs”. For example, it won’t work with numbers that have more than 1 digit. So, currently, the true scope of these “try” functions will not be able to cover every random expression you see in the wild. You would need to ensure that the tokens you see in your expression are present in the binding table. Alternatively, you could alter your expression into an “equivalent” one that would be covered by these tables. Maybe that could even be built into one of these functions.
Honestly, I’m curious what the best approach to teaching binding strengths is. When I learned APL, I did not worry myself with the exhaustive list of binding strengths. Most things just came straightforward with the right to left evaluation, and any questions I had were settled ad hoc by evaluating expressions in the session. I’m worrying that I am complicating something that should be presented in a simpler and more intuitive way. I’m going to have a discussion with my colleagues and see if we can agree on a good way to teach this. Maybe that involves creating a more complete binding table for the “try” functions. Because I do see the that these functions have the potential to be very useful. This may also involve coming up with a very simple list of the most commonly occurring precedence rules, with a link to the complete binding table for reference. Or maybe the binding strengths are all introduced in phases, instead of all at once. Will keep you posted. I will also discuss what the “proper” use and scope of these try functions should be.
Random idea: perhaps a mode that uses layered underlines to indicate binding strength.
The ideal IMO would be to have something like J’s dissect: Vocabulary/Dissect - J Wiki
Apparently that was quite a few years of work to build, however!
Hi,
In most programming languages and mathematical expressions, functions and operations are applied from left to right, following the order of operations (PEMDAS/BODMAS: Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction). This means that expressions are evaluated in the order they appear from left to right.
Well I will try to break down your expression step by step:
4 × 2: This multiplication operation is executed first, resulting in 8.5 + 3: The addition operation is performed next, giving you 8.So the final result of the expression 4 × 2 5 + 3 is indeed 8. The space between 2 and 5 does not affect the order of operations. If you want to force a specific order, you should use parentheses/brackets to group expressions and control the order of evaluation. For example, (4 × 2) + (5 + 3) would ensure that the multiplication is done before the addition.
However, I agree with the pdf https://docs.dyalog.com/latest/CheatSheet%20-%20Binding%20Strengths.pdf shared by @JoshD and I also checked this DevOps resource which it explaining it well.
Thanks
Uh, you may want to to re-read the question you’re answering (and some of the answers too). This is about APL, where PEMDAS/BODMAS doesn’t apply, and the space between 2 and 5 is very significant.
The DevOps resource you link to seems irrelevant to the subject at hand. Did you intend another link? If not, then please explain its relevance.