This is perhaps a basic question here. From the lecture notes i see that we are essentially training the last layer. When i read nn theory, the typical technique is to use backprop to compute the partial derivative term and train previous layers. I’m trying to understand the correctness in training only the last layer ?
What do we mean by fine tuning the previous layers? it is not apparent in the api that we are fine tuning the intermediate layers and last layer alone is randomly initialized.
Also i’m confused on how it is assumed for the model to have only 3 layers lr=np.array([1e-4,1e-3,1e-2]) ?
Is this because we already know that we have only 3 fully connected layers and rest are convolutions ?
Following picture shows
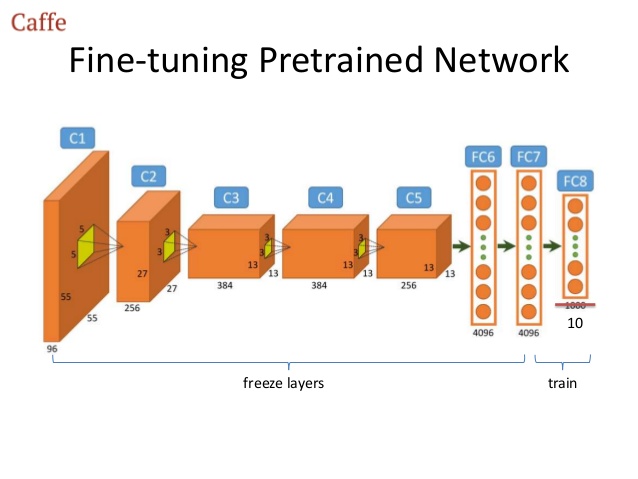
When you use backprop, you start at the last layer and you work your way back to the first layer. So if you don’t want to train all layers but only the last few layers, then you don’t need to backprop all the way, only to the last layer you want to train. So in your image, you’d stop backprop when you reach the “freeze layers”.
Usually when you have a pretrained network, you only want to train the very last layer because that needs to be specific to your data. The rest of the network can remain unchanged. However, you can also “fine-tune” those earlier layers, which is especially useful for when your data is fairly different from the data the network was pretrained on. When fine-tuning those earlier layers we only want to change them slightly, which is why we use a smaller learning rate for the first layers.
I believe the lr=np.array([1e-4,1e-3,1e-2]) refers not to 3 layers but to 3 groups of layers. The neural net used in the lesson (ResNet, I think?) is split into 3 blocks, each consisting of many layers. The first block is fine-tuned with learning rate 1e-4, the second block with learning rate 1e-3, and the final block (which includes the classifier layer) with learning rate 1e-2.
2 Likes
