Struggling to understand Direct Feedback Alignment implementation

Deep Learning
1

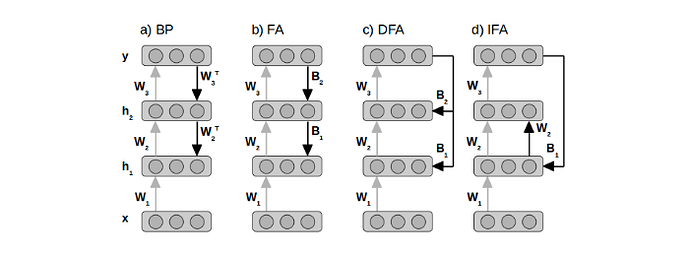
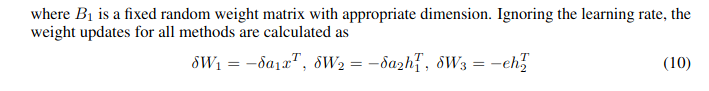I’ve been trying to branch out from learning by courses and trying to read/understand/implement from papers. I liked the idea of learning without backpropagation, found this Direct Feedback Alignment paper, and got stuck on it all of yesterday.

I’ll owe a huge debt to anyone who can clarify.

I made this Colab notebook to better share my question.

Basically, I can’t figure out how the dimensions of the matrices described in the paper could possibly be used in the calculations described in the paper.

image
image701×262 29.2 KB

What are the shapes of B2 and B1?

If I follow the equations through, I end up needing to matrix multiply B2 by the Error and then elementwise multiply that by W2.

That ends up being an equation with dimensions ?,? @ 64,1 * 64,64, and I get stuck because I can’t think of a way to matrix multiply anything by 64,1 to get 64,64. I assume there’s an implied transpose? Should I be doing 64,1 @ (64,1).T * 64,64?

2

Here’s another simple way to clarify what my confusion is.

image

The dimensions of e are the same as the output dimensions, right.

So, with batch size 64 and output dims of 1, then e is 64, 1.

image
image709×91 10.7 KB

And there, the dimensions of the weight updates for W3 are 64, 1 @ _anything_. But how can you do a weight update on W3, a hidden_dim, hidden_dim matrix, when your weight update dimensions are 64, _anything_?

3

Finally got it.

I guess you do need to take some liberties with the transformations.

I shuffled around the order of the variables and added transposes where required in order to get the dimensions to work. I guess as long as you keep the concept of “linearly transform this matrix with this matrix”, then it doesn’t really matter what order or transposition you use?