Strange behaviour in Pytorch Net

jonmunm · July 28, 2020, 1:17am

Hi,

I’ve been trying to create my first NN with Pytorch. I want to model a simple univariate Linear Regression.

However, my results are strange, if not saying erronous or weirds. This is the notebook (feel free to modify it)

The NB’s name is (Pytorch NN) Linear Regression

I watched Janani Ravi’s introductory courses about Pytorch (at the same time with fast AI v3 course)

In both courses, she uses almost the same net design and hyperparams as I use, but my result are … I don’t know how to describe them

Pls, help me figure out what is going on here

Best regards

Jonathan

PalaashAgrawal · July 28, 2020, 7:06am

Can’t access your notebooks, or the course content - Will have to sign up first. Can you please post the main neural network building code and point out what/where you feel the problem may be? Cheers!

jonmunm · July 28, 2020, 12:54pm

Sorry @PalaashAgrawal

The NB stops after 6 hours.

Best regards

jonmunm · July 29, 2020, 1:40pm

hi @PalaashAgrawal … the NB is up … have you been able to take a look at it?

Best regards

PalaashAgrawal · July 29, 2020, 2:31pm

@jonmunm

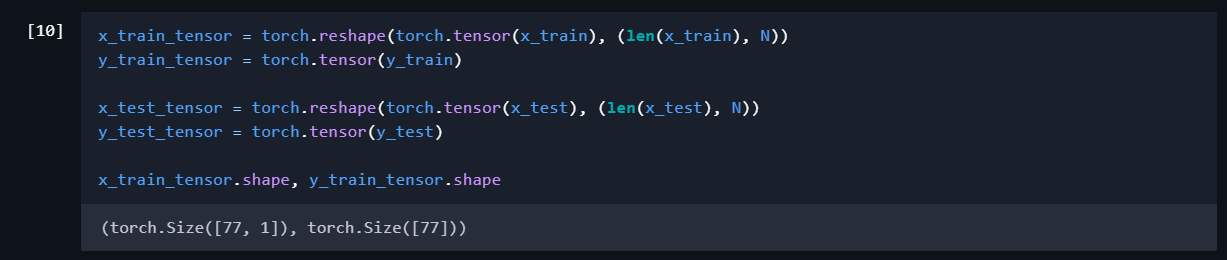
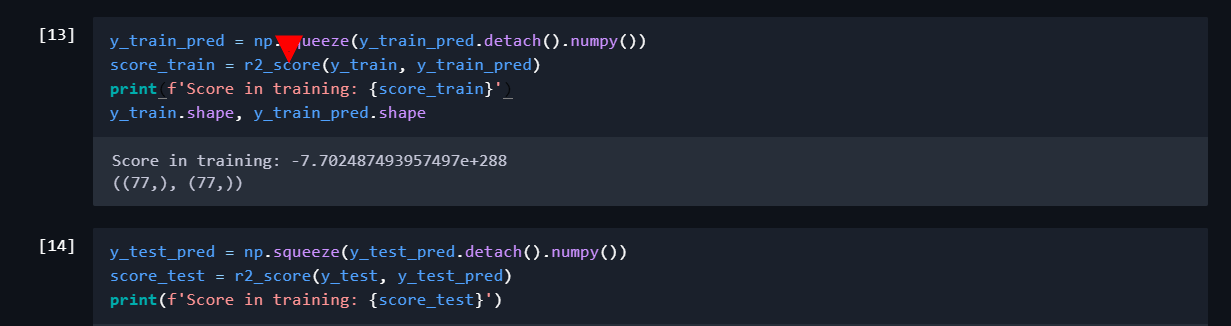
Yes. I think I see the problem. Your model output is of the shape torch.Size([77, 1]), but the targets are of size torch.Size([77]). The loss function “broadcasts” these two tensors. Basically, whenever you do an operation on two (or more) tensors/vectors/matrices, which are not of the same shape, they first need to be made of the same shape. This process is called broadcasting.

Here’s how broadcasting works: Python(more specifically numpy/PyTorch) starts from the right most dimension, and then goes left. if one of the dimensions is 1 or does not exist, then the 1 would be changed(broadcasted) to the value of the other dimension value (or if the dimension does not exist, then a new dimension is created with that value).

Here, tensors are, say, A and B, of shape [77] and [77,1] respectively, and they need to be broadcasted. So python looks at the rightmost values which is 77 for A and 1 for B.
So Python Broadcasts the tensor A over the rightmost dimension of B, making B of the shape [77,77].
Next, the other dimension is checked. which is 77 for B and non-existent for A. So, a new dimension is created in the leftmost position in A and then the leftmost dimension of B is broadcasted over the new dimension, making A of the shape [77,77].
You see, the loss function wouldn’t make any sense because of the shape of the broadcasted tensors.

You should reshape the output tensor as [77,1] too, (and [20,1] for the validation set).
Then the loss function wouldn’t have to broadcast, because both the target and the prediction would be of the size [77,1]. That should do the job.
If not, then we’d further debug for any other issues!
Cheers, stay safe

If you’re confused with how broadcasting works,or simply want to learn more, check out the numpy documentation for broadcasting

jonmunm · July 29, 2020, 4:03pm

I will apply the changes you @PalaashAgrawal … I’ll keep you updated …

Thanks very much …

Jona

jonmunm · July 29, 2020, 4:38pm

Hi @PalaashAgrawal … I did the changes … but just the broadcasting warning dissapeared …

Same results … (the NB is up)

PalaashAgrawal · July 29, 2020, 5:36pm

I dont see the changes. Maybe it takes time to update.

I also see you’ve used squeeze

squeeze removes any unit axes from the tensors, so it would turn the [77,1] back to [77]. Did you remove the squeeze operations?

jonmunm · July 29, 2020, 6:19pm

The changes were done 2 hrs ago ago …

I’ve restarted the instance … and that seems to have cleaned the cache

Best regards

PalaashAgrawal · July 29, 2020, 6:25pm

I think you’re looking for these results!

I’ll share the notebook with you. The thing that seemed to be the problem was the “reduction-'sum'” in loss_fn = nn.MSELoss(reduction=sum). I removed it(reduction = mean by default), and it seemed to work! THough i don’t know why. Ideally, it shouldn’t matter much. I’ll think over it, research, and maybe get back to you about why it is so!

jonmunm · July 29, 2020, 6:47pm

Actually … I made it work a few days ago … (I’ll will upload de NB for you to see it). Basically, I had to design a simpler NN …

Concerning your results, great … I’m very thankfull. However, I would want some explanation on why the change you did on the optimizer parameters made the net work …

If you see Janina Ravi on those Pluralsight course … Her nets works perfectly with the same desing and optimizer params …

So, I would apprecciate any info to clarify why the change you did, made the net work well

Thanks @PalaashAgrawal

Best regards

PalaashAgrawal · July 29, 2020, 6:48pm

THeoretically, there’s should be no difference in Sum of squared errors and mean of squared errors. The issue was only internal. When i checked the model parameter gradients for the SSE case, the gradients seemed to have disappeared, hence the model didn’t train at all. Perhaps the gradients values threw the model to a bad part of the loss contour. Don’t worry about it!

By the way, i didnt change the model parameters, only the loss function. And to be fair, i didnt make any changes at all- SSE and MSE should work in the same manner. As I said, the gradients vanished because of the SSE loss. Thats most probably because of the ReLU layer. When the inputs to the relu layer are all negative, then gradient simply becomes 0, and training essentially stops.

PalaashAgrawal · July 29, 2020, 6:58pm

Rest, i’d have to watch her video demo to really tell if anything was different, which is not free I think!

jonmunm · July 29, 2020, 7:22pm

Yes … it’s not free. Eventhough if you have a MS account, you could activate your Visual Studio Dev Essential and you will have one Pluralsight’s month for free …

Especifically, in both courses she desing a net for an univariate regression problem … the simplest one.

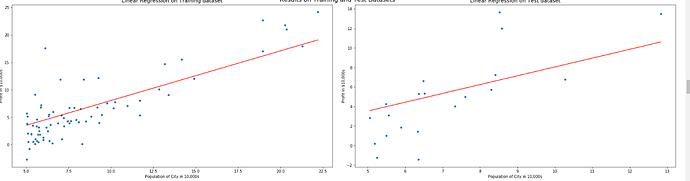
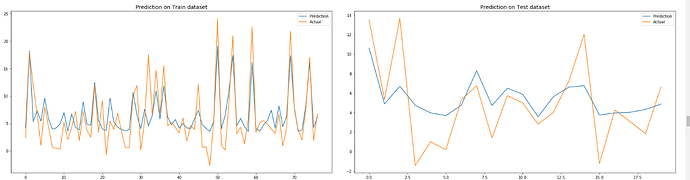
I’ll upload de other NB sooner … meanwhile, thanks and rest … Here en Chile is 15.00 hrs …

Best regards

jonmunm · July 30, 2020, 4:08pm

Hi @PalaashAgrawal …

Here I have both NB’s. The one yoo helped me improved, and the other one that worked for me by simplyfing the model

I can’t get it why you divide the loss by 100 …

Wich model es better? In terms of desing. In the end, I want to know how to desing the NN (when to add a Relu Layer or other one, etc … or how many Layer a model should have)

Best regards my friend

PalaashAgrawal · July 31, 2020, 11:54am

Hi @jonmunm
Sorry for the late reply…
I actually divided the SSE loss by 100 as a small experiment. Your input size was 77, so MSE is nothing but SSE divided by 77. I just wanted to see how the model fitting varies with the number by which we divide the SSE, and at what point the gradient vanishes. Don’t break your head over it!

Actually, the simplified model (single linear layer model) that you designed would be a safer and better choice for a simple task like linear regression. That way, you wouldn’t have to worry about the vanishing gradients that the ReLU layer was causing. Thats the reason why MSE(reduction=‘sum’) is working without any hassle.
That doesn’t mean that a more complex model isn’t the right model. Even the Neural Network model that you designed works well, maybe even slightly better. So, the choice of the model depends on the problem you’re working on. You can use a very complex model for a simple problem and get very similar results to a much simpler model. Here in your case, the choice of model simply doesn’t matter, you can’t overfit a linear regression model- infact, overfitting is the goal! But in general, JH gives some tips in choosing the right model architecture and training the model really well (Lesson 8), which i’ve summarized below.
Training a good model has 3 main steps:

Train till your model just starts overfitting. Overfitting doesn’t mean that validatoin loss >training loss. Overfitting is the stage when the validation loss consistently goes up!
Reduce the overfitting.
Tweak the model according to your problem

Reducing overfitting is not easy, and has multiple steps. JH also gives a useful sequential guide to go through this process.

a. Get more data (if you can!)
b. augment the data (transformation, etc) (again, if possible)
c. Train on a generalizable architecture (This is where your concern comes in. A generalizable architecture is an architecture that is known to work well on most problems in the domain. For example, a single hidden layer Neural Network is known to work well in most simple tasks. So start with that, unless the problem demands making some exceptions, like in your case, where even a linear layer without any actuvation function seemed to do the job!). Similarly, for Image classification tasks, go for Resnets or other generalized architectures- why not? They’ve proved to work well in the past!
d. Regularize the model. Most people do it before everything else, which only reduces the model ability. The model is of no use if you’re not taking full advantage of its ability to predict. THis process includes weight decay, dropout, etc.
e. Reduce the Architectural complexity to better fit the complexity of your particular task. This should be done last. Unless the model is so complex that training is slow, or the loss landscape is very jittery. This is a secondary method to reduce overfitting. Regularization is the primary method. Similarly, data augmentation is a primary method of reducing overfitting.

Cheers! Hope it gives some insights.
In the end, I only want you to take this away with you: go with models that are known to work well(like Resnets for Image classification problems, and so on)

jonmunm · July 31, 2020, 1:44pm

My friend…

I’ve been in both forums, here and Pytorch’s. THIS is the response I was looking for . So, I will continue with v3 coders’s course (I stopped at lesson 3, because there were some issues I could’t understand well … So, I’ll watch the course completely, without coding, and then I’ll watch them it again)

Thanks @PalaashAgrawal …

Best regards