Regarding Fast.ai's optimal learning rate finder using loss-vs-lr plot

Part 1 (2018)
1

Well, this topic had been mentioned before here but since the thread is inactive, I’ll post it again.

The lr_find method mentions that it uses the paper Cyclical Learning Rates for Training Neural Networks to find the optimal learning rate but, the actual purpose of the paper is to remove the need to guess any learning rate whatsoever.
Here is a quote from the abstract of the paper:

This paper describes a new method for setting the learning rate, named cyclical learning rates, which practically eliminates the need to experimentally find the best values and schedule for the global learning rates.

And according to lr_find, it uses this same paper to find the optimal learning rate.

Also, cyclical learning rate is a scheduler to vary the learning rate during training rather than to find the optimal learning rate before training the model.
The paper only describes mechanism to find this lr interval (max_lr and base_lr) but doesn’t mention anything about the optimal learning rate. And for this, it uses the accuracy vs lr plot rather than using the loss vs lr to find the lr interval.
Here is the figure:
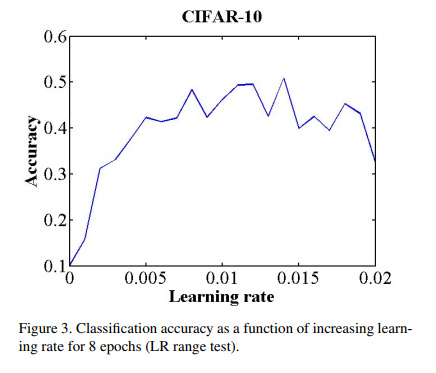
image

Also, like jeremy mentions, it doesn’t even use the steepest incline as the max_lr but actually recommends it as:

Next, plot the accuracy versus learning rate. Note the learning rate value when the accuracy starts to increase and when the accuracy slows, becomes ragged, or starts to fall. These two learning rates are good choices for bounds; that is, set base lr to the first value and set max lr to the latter value

It merely says to use the first lr that it finds as base_lr and then use the lr when the accuracy begins to become jagged as the max_lr.

It may just be that I don’t know much and as such I really can’t understand this paper or that maybe Jeremy misquoted the paper?
If anyone knows where the optimal learning rate finder paper is, a little help would be greatly appreciated.

2 Likes
2

Also, in the second lecture, Jeremy mentions that the technique is a small part of a paper that wasn’t primarily about setting learning rates, so it seems unlikely that the technique comes from a paper with the title “Cyclical Learning Rates for Training Neural Networks”. He does claim in both lectures 1 & 2 that the author of the technique is Leslie Smith, who is in fact the author of the cyclical learning rates paper. I’m going to have a look through Leslie’s work and see if I can figure this out. Here’s a link to all of Leslie’s papers on Arxiv: https://arxiv.org/search/cs?query=Leslie+Smith&searchtype=author&abstracts=show&order=-announced_date_first&size=50

3

I see. I didn’t notice that that was what Jeremy said.
I’ll check out other papers too and post it here if I find it.

4

At 11:40 into the second lecture he says “in fact even this particular technique was one subpart of a paper that was about something else”. Very strange. Both the first lecture and the notebook clearly state that he’s getting the technique from that cyclical learning rates paper.

5

Ok, I think I’ve figured out the confusion. Read the last paragraph from section 3.3 of the paper.

“Whenever one is starting with a new architecture or dataset, a single LR range test provides both a good LR value and a good range. Then one should compare runs with a fixed LR versus CLR with this range. Whichever wins can be used with confidence for the rest of one’s experiments.”

So the paper is primarily about varying the learning rate cyclically, but he does say that you can use the learning rate vs. loss test to potentially find the best fixed learning rate.

6

It seems a little redundant to train a model from scratch after using the learn.lr_find function since it has already preformed some training. Can’t we simply extend the training session of the learn.lr_find function using the chosen learning rate?

7

Implement it yourself and you can do it :slight_smile:

8

I had forgotten about this completely :joy:

9

This paper mentions in paragraph 3.3 an empirical method to find base_lr and max_lr, the bounds between which the cyclical learning rate will vary (find_lr does exactly the same, besides it uses the loss instead of the accuracy of I am right). The author doesn’t explain theoretically why it works and how to chose exactly those bounds (just look on the plot and take values that look OK) but it makes intuitively sense and seems to work empirically good.

1 Like