Hello everyone!
I am interested in modelling physical/dynamic systems with deep learning, and I think that recurrent neural networks should be a good way to model systems that can be normally represented by state-space models. In short, you have system with a state that evolves following some equations, and I would like the model to learn these, in a non-parametric way. Deep learning is known to be a universal function approximator, so it should work, shouldn’t it? 
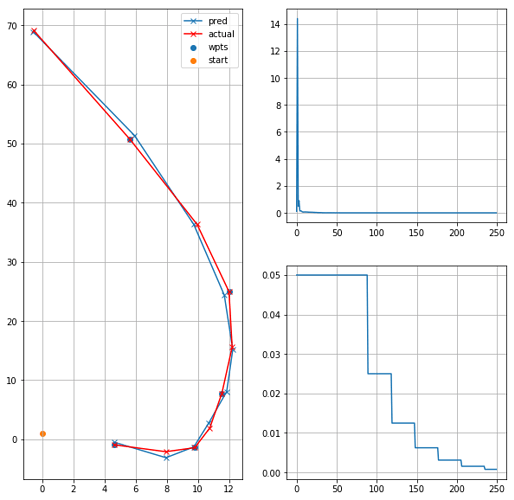
As first experiment I am trying to have a model to learn how a mobile object follows a path, given points of this path (like waypoints). As a synthetic example, I generated a 2D curve, and as first step I want to overfit to a single example. (I know that the curve generated this way is not following dynamic equations, but for the exercise I think it fits without problem. For a next step I would generate them from dynamic equations).
In the repo’s notebook I have the code to generate the synthetic example, a simple stacked RNN network (in keras, but I plan to do it also with pytorch, and if I find out how to, with the tools coming from fastai).
About the input, I am giving the initial point of the object, and the points that will be crossed by it. I repeat the input since I don’t know how to do it other way:
- The initial position: I cannot set an internal state of the RNN to it, because I don’t know how the network will store it’s position. Also, I don’t know how to give something once as initial data to a network and then let it run iteratively. Doing a one-to-many model would work, but eventually I will want to give inputs online to the model, like forces applied externally, and the like, so I have to use a many-to-many approach.
- The waypoints: actually is just as with the initial position. I don’t know a better way to provide them other than repeating them in the input.
The output is obviously the path that the object will follow.
This is an example of the path to be learnt and the network output (reproducible in the notebook):
My findings trying combinations of size (layers and units) of the network, and of the data sample, is that:
- If the path has a few points (for example 10 or 20) and 5 waypoints, the network will learn it consistently.
- With 100 points, I cannot make it learn the single sample, it always finds a local optimum by “going” to the centroid of all the path points.
- In the middle between those, it can converge sometimes, but it’s highly dependant on the random values from initialization. I tried different initializers (he and glorot, uniform and normal), and I have the impression that uniform tends to work better, but I need more experiments.
Has someone have tried to model this kind of system? Am I approaching this in a proper way? And, obviously, does it seems like what it’s implemented is what I describe? (I would say so, or it wouldn’t have converged in the easier cases … ). Why it doesn’t converte for long tracks, independently of network size?
Thank you for any help/idea/suggestion!
The code and findings commented are in this repo: