Hello all,
An idea for modelling long-range interactions in CNNs came to my mind, and I thought to share it with you folks and seek your opinions.
On a high level, it functions akin to squeeze-and-excitation, where the chief difference is instead of calibrating channel-wise features, it operates on spatial features. Concretely, assume we start with a 3 X 256 X 256 tensor; the first step is to squeeze the channels via a convolution to get a 256 X 256 tensor. However, owing to the computational costs of the multilayer perceptron that is about to follow, it is necessary to downscale the spatial dimensions, which can be done by setting the convolution’s kernel size and stride to, say, 16 (i.e., the input is being “patchified”). The resulting 16 X 16 matrix is flattened to yield a 256-dimensional vector that goes through an MLP with one hidden layer, plus a final sigmoid activation. Finally, the vector is reverted back to 16 X 16, and each pixel in the original input is multiplied by its corresponding weight.
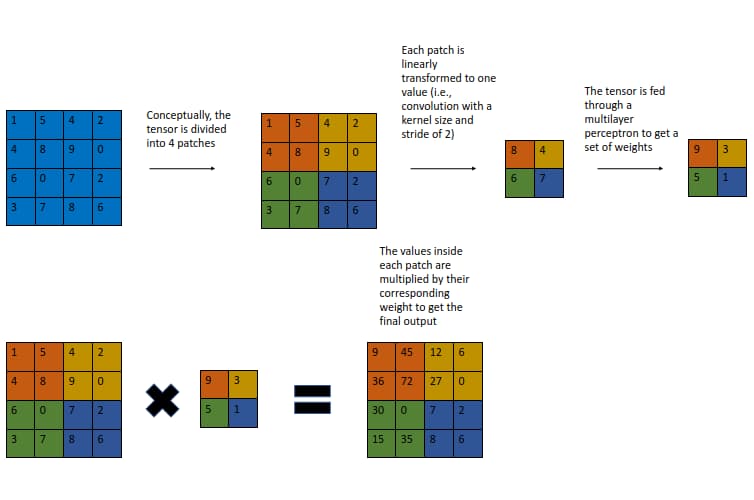
Below is a sketch of this concept where the input is 4 X 4 (single-channelled for simplicity), each patch is 2 X 2 rather than 16 X 16, and sigmoid is omitted.
This block, which I am dubbing the patch spatial interaction (PSI) module, is by no means novel, and similar ideas include gather-and-excite, global context networks, and so on. Nevertheless, I have pitted ResNets with PSI against some networks I use frequently (e.g., NF-Nets* and ECA-Nets), and the PSI-based models consistently outperformed the other ones by a significant margin whilst being more efficient on multiple classification datasets.
For instance, on Caltech-101 and within 50 epochs, a PSI-ResNet-14 with 8434057 parameters and a training time of 997 seconds obtained the same accuracy (0.72) as the best non-PSI model, an NF-ResNet-50, which has 23714981 parameters and took 1876 seconds to train. Moreover, a PSI-ResNet-26 with 14575469 parameters clocked at 1438 seconds and attained an accuracy of 0.76.
The GitHub repository includes the code as well as all the benchmarks.
Training a PSI model on ImageNet is something I would love to do, but I do not have the resources to do so currently, and this was the best I could pull off; what are your thoughts?
Thank you!
*Normalization-free networks utilize adaptive gradient clipping for training with strong augmentation and large batch sizes, but it didn’t improve performance in this case (likely because the batch size is merely 32), so it was removed to keep the code clean.