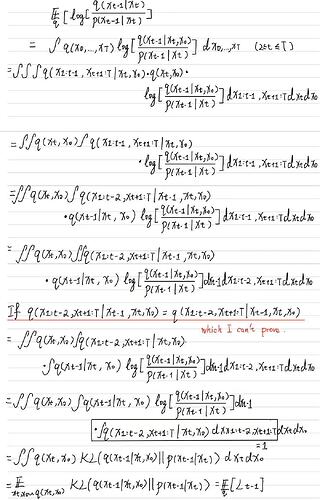I am trying to understand the DDPM paper. And I also tried to derived some of the equations mentioned in the paper. In the paper, the upper bound of the negative log likelihood was splitted into the expectation of the three KL divergence terms. More specifically:
\begin{align} \mathbb{E}_q[-logp_{\theta}(x_0)]\leq& \mathbb{E}_q[-log\frac{p(x_T)}{q(x_T|x_0)} - \sum_{t>1}log\frac{p_\theta(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)} - logp_\theta(x_0|x_1)] (1)\\ \leq&\mathbb{E}_q[D_{KL}(q(x_T|x_0) ||p(x_T)) + \sum_{t>1}D_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t)) - logp_\theta(x_0|x_1)](2) \end{align}
I am having trouble in understanding the transformation from (1) to (2).
If we expand \mathbb{E}_q[...]:
\begin{equation}\mathbb{E}_q[...] = \int q(x_{0:T})\cdot(...)dx_{0:T}\end{equation}
And the defination of the KL divergence is:
D_{KL}(q(x)||p(x)) = \int q(x)\cdot log\frac{q(x)}{p(x)}dx
Let’s look at the fraction between the reverse process that are being learned and the forward process given x_0:
\begin{align}
\mathbb{E}_q[-\sum_{t>1}log\frac{p_\theta(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)}] &= \mathbb{E}_q[\sum_{t>1}log\frac{q(x_{t-1}|x_t,x_0)}{p_\theta(x_{t-1}|x_t)}]\\
&= \sum_{t>1}\int q(x_{0:T})\cdot log\frac{q(x_{t-1}|x_t,x_0)}{p_\theta(x_{t-1}|x_t)}dx_{0:T}
\end{align}
Accroding to the paper:
\begin{align} \mathbb{E}_q[-\sum_{t>1}log\frac{p_\theta(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)}] &= \mathbb{E}_{q'}[\sum_{t>1}D_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t))] \\ &=\mathbb{E}_{q'}[\sum_{t>1}L_{t-1}] \end{align}
It is apparent that \mathbb{E}_q[...] must be different from from the the \mathbb{E}_{q'}[...]. My goal is to find the expression of \mathbb{E}_{q'}[...].
In the Appendix of the DDPM paper, the author quoted the derivations is from Sohl-Dickstein et al. [53]; So I scanned through this paper and found (in equation (51) of the paper):
\begin{align} \mathbb{E}_q[-\sum_{t>1}log\frac{p_\theta(x_{t-1}|x_t)}{q(x_{t-1}|x_t,x_0)}] &= \sum_{t>1}\int \int q(x_0, x_t)D_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t)) dx_t dx_0 \end{align}
Therefore, \begin{equation}\mathbb{E}_{q'}[...] = \int \int q(x_0, x_t) \cdot (...) dx_t dx_0 \end{equation}
Now, it is my attempt to derive \mathbb{E}_{q'}[...].
I failed to do so, there is a bottleneck where it seems like q(x_{1:t-2}, x_{t+1:T}|x_{t-1}, x_t, x_0) = q(x_{1:t-2}, x_{t+1:T}|x_t, x_0) has to be true to make my derivation complete. And I have no idea how to show this. It has bothered me for a long time.
I applogize if there is any native problem in the derivation. My math knowledge is not profound. I have searched for a solution for days. Asking in the forum really is my last resort.
I really appreciate any help or insight that can be brought to me in this post ![]()