`metric` printed during training does not equal a calculation of the same metric after loading the model saved with `best_save_name`

zache · October 8, 2018, 9:00pm

This might be a really stupid question, but when you pass in a metric, such as RMSE, how is it being calculated during training?

During training I am getting pretty good results, but then when I call .predict() on the model (loaded via best_save_name), and manually calculate the RMSE using the same function, I am getting a completely different number (and I’m using the same validation indices for y_true).

Also, when validating (at the end of each epoch during training), it iterates through 1236 validation samples which, with a batch size of 128, accounts for only 17.5% of my data (and is only half of my validation size, which is 35%).

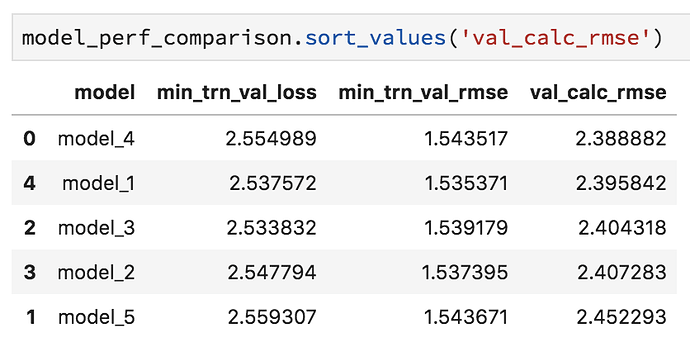
Here is a screenshot of the min loss and rmse shown during training vs the rmse calculated with the best save:

As you can see, there isn’t even a relationship between the best performance…

So I really have no idea how this is being calculated during training! I really hope someone can clarify what is probably a simple misunderstanding.

Thank you!!

Edit: and just to make sure there is no bug in how I’m calculating the loss of the saved models, here is the function:

def load_model_get_val_rmse(saved_weights, loc_val_idx):

    # init model objects
    md = ColumnarModelData.from_data_frame(path = 'models', val_idxs = loc_val_idx, df = df,
                                           y = yl.astype(np.float32), cat_flds = cat_vars,
                                           bs = 128, test_df = df_test)
    m = md.get_learner(emb_szs = emb_szs, n_cont = len(df.columns) - len(cat_vars),
                       emb_drop = 0.04, out_sz = 1, szs = arch, drops = dropout, y_range = y_range)

    # load saved weights
    m.load(saved_weights)

    # calc rmse
    yl_true = deepcopy(yl[loc_val_idx])
    yl_pred = deepcopy(m.predict().reshape(-1,))
    error = rmse(yl_pred, yl_true)

    return error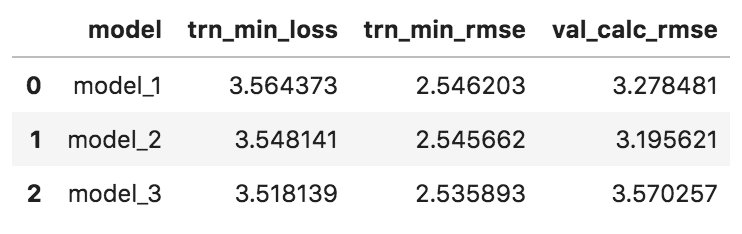

stephenjohnson · October 8, 2018, 9:43pm

For validation the batch size gets multiplied by 2 under the premise that since gradients don’t need to be calculated the batch size can be increased due to less memory consumption.

def __init__(self, path, trn_ds, val_ds, bs, test_ds=None, shuffle=True):
    test_dl = DataLoader(test_ds, bs, shuffle=False, num_workers=1) if test_ds is not None else None
    super().__init__(path, DataLoader(trn_ds, bs, shuffle=shuffle, num_workers=1),
        DataLoader(val_ds, bs*2, shuffle=False, num_workers=1), test_dl)

zache · October 9, 2018, 11:40am

Thanks – that explains one aspect of the mystery!

But then how is the metric calculated during validation? Is it the average of each batch? Or is it over the entire validation set?

One of the most likely disparities is how best_save_name is saving the best model… Is it at the end of each epoch? If that’s the case then it really doesn’t make sense why the calculations are so different…

zache · October 9, 2018, 11:43am

I have a feeling that I’m calculating RMSE wrong because the RMSE that is printed out during training is what I’d expect to see and the calculated is not. But I really have no idea what I’m doing wrong…

stephenjohnson · October 9, 2018, 5:04pm

Looking at the code, metrics appear to be calculated per batch and then averaged together. Not sure if that explains the discrepancy though.

From validate method in model.py (line 242)

return [np.average(loss, 0, weights=batch_cnts)] + list(np.average(np.stack(res), 0, weights=batch_cnts))

Full validate method.

def validate(stepper, dl, metrics, epoch, seq_first=False, validate_skip = 0):
    if epoch < validate_skip: return [float('nan')] + [float('nan')] * len(metrics)
    batch_cnts,loss,res = [],[],[]
    stepper.reset(False)
    with no_grad_context():
        t = tqdm(iter(dl), leave=False, total=len(dl), miniters=0, desc='Validation')
        for (*x,y) in t:
            y = VV(y)
            preds, l = stepper.evaluate(VV(x), y)
            batch_cnts.append(batch_sz(x, seq_first=seq_first))
            loss.append(to_np(l))
            res.append([to_np(f(datafy(preds), datafy(y))) for f in metrics])
    return [np.average(loss, 0, weights=batch_cnts)] + list(np.average(np.stack(res), 0, weights=batch_cnts))

zache · October 9, 2018, 7:28pm

Thanks again! It actually could explain some of the discrepancy, but when I run the data through a RF I’m getting a similar error to what is printed during training so it still leads me to believe that I’m somehow calculating it incorrectly.

How does calling eval() on the model before getting predictions help?

It seems the two most likely possibilities are:

I’m getting the predictions of the validation set incorrectly
best_save_name is doing something different than keeping (saving) the best model at the end of each epoch

And that leads me to two questions:

What is the best way to get the predictions of the validation set of a saved and reloaded model?
What is best_save_name doing?

stephenjohnson · October 10, 2018, 2:26am

I’m not sure but I think I may have found the issue. When you use best_save_name and if you haven’t specified any additional metrics then it will use the loss to determine the best model to save. It will use the model with the least loss. However, if you specify other metrics then it will use the first metric specified, BUT, it assumes this metric is accuracy and so saves the model with the greatest accuracy. In your case, your metric is rmse and you want it to be the model with the smallest rmse, but it is saving the model with the greatest rmse. I’ve pasted the code below. You could try modifying the save_when_acc method in sgdr.py and switching the greater than (>) with a less than (<) and see if it fixes your issue.

def __init__(self, model, layer_opt, metrics, name='best_model'):
    super().__init__(layer_opt)
    self.name = name
    self.model = model
    self.best_loss = None
    self.best_acc = None
    self.save_method = self.save_when_only_loss if metrics==None else self.save_when_acc
    
def save_when_only_loss(self, metrics):
    loss = metrics[0]
    if self.best_loss == None or loss < self.best_loss:
        self.best_loss = loss
        self.model.save(f'{self.name}')

def save_when_acc(self, metrics):
    loss, acc = metrics[0], metrics[1]
    if self.best_acc == None or acc > self.best_acc:
        self.best_acc = acc
        self.best_loss = loss
        self.model.save(f'{self.name}')
    elif acc == self.best_acc and  loss < self.best_loss:
        self.best_loss = loss
        self.model.save(f'{self.name}')

zache · October 10, 2018, 12:07pm

Damn I think you’re right. This has to be it. It actually makes a lot of sense because some of the more complex models (two layers, many nuerons) that were getting really good results during training but bad results with the manual calculation were over-fitting by the end of the training cycle (was doing a 1cycle grid search with a static cycle length and no early stopping). Really good find!!

I’d go as far as saying that’s a pretty big bug as most structured data will be a regression problem (and many classification problems are using logloss)… But maybe most people are using this library for CV and NLP (or nobody is actually saving (re: using) their models )… I’ll test this out with a few models and get back to you to confirm if this helps

Thanks again!!

zache · October 10, 2018, 3:29pm

Well I had a lot of hope, but it doesn’t seem like this fixed the discrepancy

The models are named according to best training RMSE (i.e. model_1 has the lowest training error and model_5 has the worst training error) and then sorted according to the calculated RMSE after a save and load of the “best model” (quotations are really necessary/appropriate here):

Unfortunately, there doesn’t seem to be any relationship to either training loss or training RMSE.

FYI: Instead of modifying the source code, I just used neg_rmse as the metric – which should work with the maximization logic in best_save_name (as is fine in sklearn).

I’m so frustrated with this… Had a lot of hope with that one.

Next I’ll try:

Comparing the calculated RMSE (via .predict()) of the same model: “NOT saved-reloaded” vs “saved-reloaded”
Adding some print statements to the best_save_name code and see if everything is being calculated as we think it is.

If everything checks out there then the problem lies somewhere in loading the model or calculating the predictions on the validation set with the respective model. The calculated RMSE is so far off of the training RMSE it’s seeming fairly likely at this point.

I don’t suppose you or anyone else has any thoughts here…

A last resort could be ditching using metric during training and see if that works better but I’m not feeling too confident that will work either at this point (and it’s frustrating to not have visibility of the target metric).

Thanks again for your help though I really appreciate you spending some time trying to help me figure this out!

zache · October 10, 2018, 6:03pm

So it seems that the problem has nothing to do with best_save_name (though switching to a metric that is maximized is probably still necessary).

Instead of saving the model and reloading it, I just trained it and called .predict() on the trained model and calculated RMSE manually as I was before. Doing that also results in the big discrepancy was seen before.

That means:

There is a problem with .predict(), or
There is a problem with how I am manually calculating the error

Code / Output:

# params
arch = [1024, 512]
dropout = [0.01, 0.01]
wd = 1e-3
cycle_len = 20

# init model
md = ColumnarModelData.from_data_frame(
    path = 'models',
    val_idxs = val_idx,
    df = df,
    y = yl.astype(np.float32),
    cat_flds = cat_vars,
    bs = 128,
    test_df = df_test
)
m = md.get_learner(
    emb_szs = emb_szs,
    n_cont = len(df.columns) - len(cat_vars),
    emb_drop = 0.04,
    out_sz = 1,
    szs = arch,
    drops = dropout,
    y_range = y_range
)

# fit model
m.fit(
    lrs = 1e-4,
    n_cycle = 1,
    cycle_len = cycle_len,
    wds = wd,
    use_wd_sched = True,
    use_clr_beta = (10, 10, 0.95, 0.85),
    metrics = [neg_rmse],
    best_save_name = 'full_features_1cycle_wdgs_wd{}_drop{}_{}'.format(wd, dropout[0], dt_str)
)

OUTPUT:

epoch      trn_loss   val_loss   neg_rmse   
    0      2.609511   2.937018   -1.648727 
    1      2.752639   2.67689    -1.582182 
    2      2.72121    2.638024   -1.567019 
    3      2.824484   2.616868   -1.564888 
    4      2.47538    2.629752   -1.564153 
    5      2.577455   2.627117   -1.569332 
    6      2.241886   2.895021   -1.626933 
    7      2.10251    2.721892   -1.58121  
    8      2.109852   2.899992   -1.659028 
    9      2.317027   2.68414    -1.589611 
    10     1.886544   2.651551   -1.572613 
    11     1.917104   2.645287   -1.561865 
    12     1.897094   2.672715   -1.57557  
    13     1.77871    2.663678   -1.569883 
    14     1.755695   2.729286   -1.591549 
    15     1.771692   2.69475    -1.575213 
    16     1.375698   2.739276   -1.588298 
    17     1.524395   2.762004   -1.597092 
    18     1.238112   2.770292   -1.599913 
    19     1.204172   2.772468   -1.599469 

[array([2.77247]), -1.5994691769563205]

ERROR CALCULATION WITH .predict():

# calc rmse
yl_val = deepcopy(yl[val_idx])
yl_hat = deepcopy(m.predict().reshape(-1,))
abs(neg_rmse(yl_hat, yl_val))

OUTPUT:

2.4884370483877265

stephenjohnson · October 10, 2018, 6:21pm

Can you try verifying that the yl[val_idx]) order and the order that m.data.val_dl order are the same? I’m wondering if perhaps they aren’t returned in the same order you’re expecting. Try iterating over m.data.val_dl and match them up with vl[val_idx].

stephenjohnson · October 10, 2018, 6:27pm

You could also try using predict_with_targs(m, dl) and passing in the model and the data loader yourself. This version should return the predictions and the y values and then you can do the rmse metric on that and see if those values match up to what you are expecting.