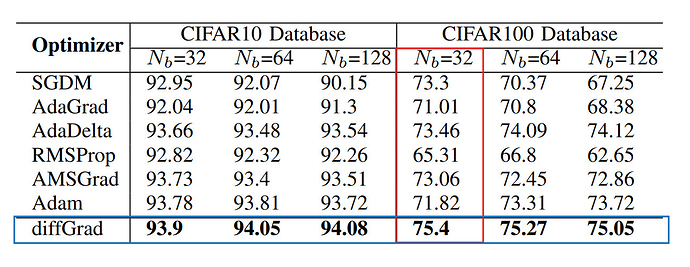
Critical Review of DiffGrad:
I have been playing with diffgrad and subsequently trying to build improved optimizer based on the fundamental intuition on top of which diffgrad is built. First concern, diffgrad is always deaccelerating the learning rate because ξ is always less than 1, additionally, it runs into a risk of getting stuck in a local minima because of severely decreasing the ξ parameter because of the sigmoid operation.
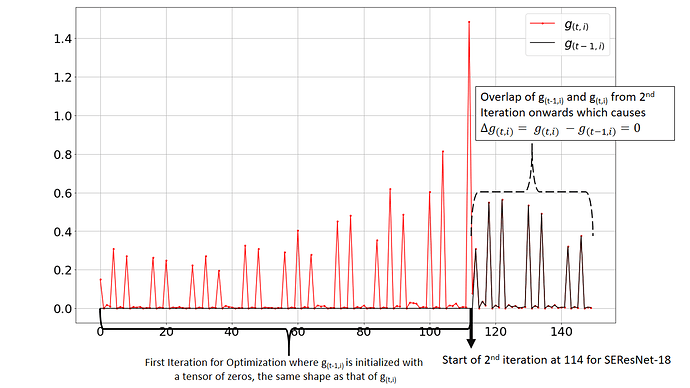
Follow up on the official code implementation of diffgrad which can be found here, I observed some strong issues. During plotting the current step’s gradient g(t,i) and previous step’s gradient g(t-1,i), I observed that after the first iteration both the plots overlap on each other, thus resulting in the ΔG = g(t,i) - g(t-1,i) to be 0 which is incorrect because the graph of g(t-1,i) should be the replica of g(t,i) but just right shifted by 1 unit where 1 unit is the length of group[‘params’] because for the first iteration all the parameters (p1, p2, p3,…, pn) have the previous gradient g(t-1,i) to be initialized with a tensor of zeros of the same shape as that of the current gradient g(t,i). The plot obtained from the original implementation of diffgrad is shown below:
Investigating this I realize that this issue is caused by Call by reference which makes both prev_grad g(t-1,i) and current grad g(t,i) to overlap and thus the difference becomes zero.
Fixing this was easy where one has to use the .clone() function wherever previous_grad is updated/ initialized. It should like this:
state['previous_grad'] = grad.clone()
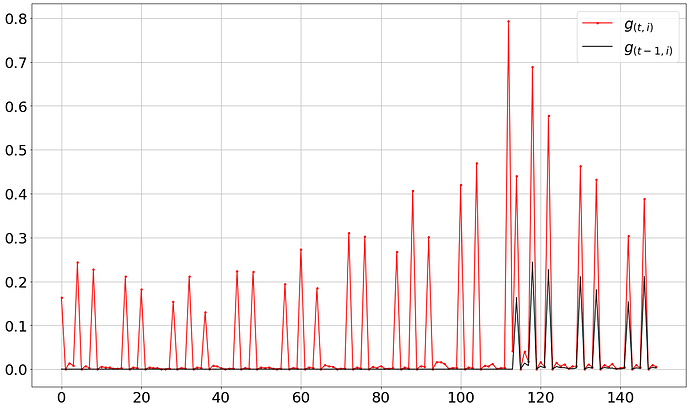
Now, using this fixed code, one can observe the correct trend in the graph as per the expected behavior as shown below:
I did a test run with the original implementation and the fixed implementation for CIFAR-10 using SEResNet-18 for 10 epochs using a Batch Size of 32 and lr = 0.001.
Original Implementation: Test Accuracy - 84.38%
Fixed Implementation: Test Accuracy - 83.42%
Adam: Test Accuracy - 84.27%
Interesting Observation:
Since, for the 1st iteration spanning for the length of group['params'], the previous grad is 0 so finding ΔG = g(t,i) - g(t-1,i) makes no sense because ΔG will always be equal to g(t,i). For a simple network like SEResNet-18, this unnecessary subtraction is computed for 114 times per optimization complete cycle.
Conclusion:
If the paper used the original implementation to obtain the results showcased, then all of them are incorrect. Additionally, all custom optimizers @LessW2020 has built using the base of diffgrad like DiffMod (Diffgrad + AdaMod) which can be found here and Diff_RGrad (Diffgrad + RAdam) which can be found here are also incorrect.
My colleague at Landskape (Manjunath Bhat) raised the issue in the original source repository of Diffgrad which can be found here. The author in reply stated that with the updated (fixed) implementation, they are reporting better scores than what mentioned in the paper. However, this should be further tested and validated.
For reference, the fixed code for Diffgrad is:
import math
import torch
from torch.optim.optimizer import Optimizer
import numpy as np
import torch.nn as nn
class diffgrad(Optimizer):
r"""Implements diffGrad algorithm. It is modified from the pytorch implementation of Adam.
It has been proposed in `diffGrad: An Optimization Method for Convolutional Neural Networks`_.
Arguments:
params (iterable): iterable of parameters to optimize or dicts defining
parameter groups
lr (float, optional): learning rate (default: 1e-3)
betas (Tuple[float, float], optional): coefficients used for computing
running averages of gradient and its square (default: (0.9, 0.999))
eps (float, optional): term added to the denominator to improve
numerical stability (default: 1e-8)
weight_decay (float, optional): weight decay (L2 penalty) (default: 0)
amsgrad (boolean, optional): whether to use the AMSGrad variant of this
algorithm from the paper `On the Convergence of Adam and Beyond`_
(default: False)
.. _diffGrad: An Optimization Method for Convolutional Neural Networks:
https://arxiv.org/abs/1909.11015
.. _Adam\: A Method for Stochastic Optimization:
https://arxiv.org/abs/1412.6980
.. _On the Convergence of Adam and Beyond:
https://openreview.net/forum?id=ryQu7f-RZ
"""
def __init__(self, params, lr=1e-3, betas=(0.9, 0.999), eps=1e-8, weight_decay=0):
if not 0.0 <= lr:
raise ValueError("Invalid learning rate: {}".format(lr))
if not 0.0 <= eps:
raise ValueError("Invalid epsilon value: {}".format(eps))
if not 0.0 <= betas[0] < 1.0:
raise ValueError("Invalid beta parameter at index 0: {}".format(betas[0]))
if not 0.0 <= betas[1] < 1.0:
raise ValueError("Invalid beta parameter at index 1: {}".format(betas[1]))
defaults = dict(lr=lr, betas=betas, eps=eps, weight_decay=weight_decay)
super(diffgrad, self).__init__(params, defaults)
def __setstate__(self, state):
super(diffgrad, self).__setstate__(state)
def step(self, closure=None):
"""Performs a single optimization step.
Arguments:
closure (callable, optional): A closure that reevaluates the model
and returns the loss.
"""
loss = None
if closure is not None:
loss = closure()
for group in self.param_groups:
for p in group['params']:
if p.grad is None:
continue
grad = p.grad.data
if grad.is_sparse:
raise RuntimeError('diffGrad does not support sparse gradients, please consider SparseAdam instead')
state = self.state[p]
# State initialization
if len(state) == 0:
state['step'] = 0
# Exponential moving average of gradient values
state['exp_avg'] = torch.zeros_like(p.data)
# Exponential moving average of squared gradient values
state['exp_avg_sq'] = torch.zeros_like(p.data)
# Previous gradient
state['previous_grad'] = torch.zeros_like(p.data)
exp_avg, exp_avg_sq, previous_grad = state['exp_avg'], state['exp_avg_sq'], state['previous_grad'].clone()
beta1, beta2 = group['betas']
state['step'] += 1
if group['weight_decay'] != 0:
grad.add_(group['weight_decay'], p.data)
# Decay the first and second moment running average coefficient
exp_avg.mul_(beta1).add_(1 - beta1, grad)
exp_avg_sq.mul_(beta2).addcmul_(1 - beta2, grad, grad)
denom = exp_avg_sq.sqrt().add_(group['eps'])
bias_correction1 = 1 - beta1 ** state['step']
bias_correction2 = 1 - beta2 ** state['step']
# compute diffgrad coefficient (dfc)
diff = abs(previous_grad - grad)
dfc = 1. / (1. + torch.exp(-diff))
state['previous_grad'] = grad.clone()
# update momentum with dfc
exp_avg1 = exp_avg * dfc
step_size = group['lr'] * math.sqrt(bias_correction2) / bias_correction1
p.data.addcdiv_(-step_size, exp_avg1, denom)
return loss