Sarada has set a great example on how to visualize ReLU to enhance understanding. Here let’s try to do the same to Momentum.
What does Momentum look like
momentum = exponentially weighted moving average
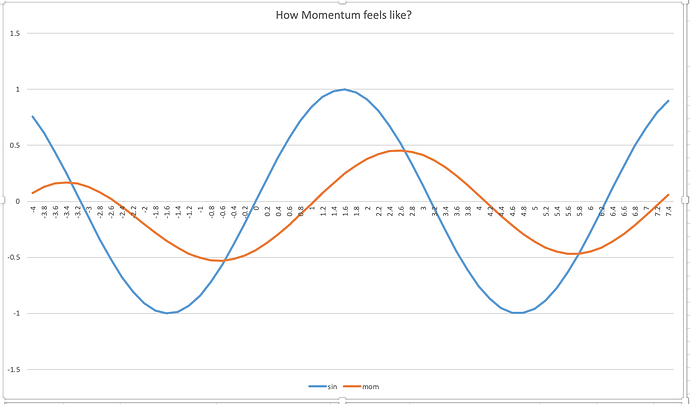
Basically, you can apply Momentum to a wiggly line. In the first example below we are using momentum to smooth y = sin(x) out. It smooths the line by give a large weight (in deep learning the convention is 90% on the previous momentum value and 10% weight to sin(x). so we have the momentum formula to be
Why need momentum in deep learning?
We use SGD to update weights using derivatives. Derivatives like to swing between large positive and negative values. As a result, weight values swing too.
The intuition of momentum I suspect to be:
Weights jumping back and forth in big steps won’t bring them to the optimal efficiently. But if weights can keep their movement momentum, and gradually increase the steps, there should be higher chance of getting to the optimal.
First Example: Let’s visualize the momentum function
In this experiment we apply momentum formula to a sine function, and plot it to see how they look. Note: I set the first original momentum value to be 0
Can you get a feel about how momentum smooth things out or keep the momentum of previous state from the graph below?
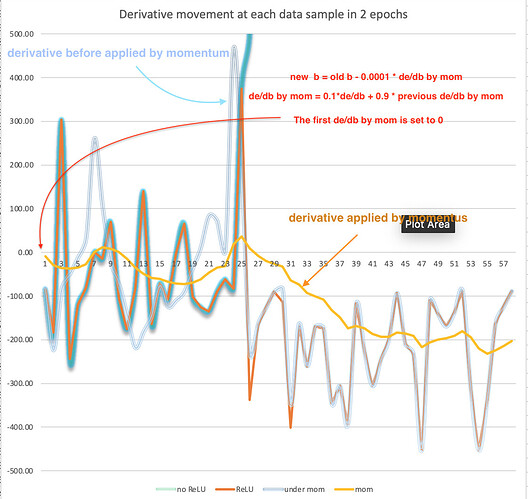
Second Example: Let’s visualize momentum when applied on derivatives of weight
The derivatives of weights on each data point can be very wiggly. I have plotted the derivatives of weight d on our 2-neuron model. Their only difference is whether they use ReLU and Momentum or not. “no ReLU” is a derivative in the model without ReLU, “ReLU” means a derivative in the model with ReLU, “under mom” means a derivative in the model using ReLU and Momentum, “mom” means the momentum value in the model using ReLU and Momentum.
You can try out the spreadsheet above from here on the worksheet named “Plot momentum”
How Jeremy taught momentum? 2018, 2019
Jeremy explained the use of momentum in two use cases which I only came to get my head around them when I do this experiment today. (Please correct me if I am still not accurate in my understanding on them)
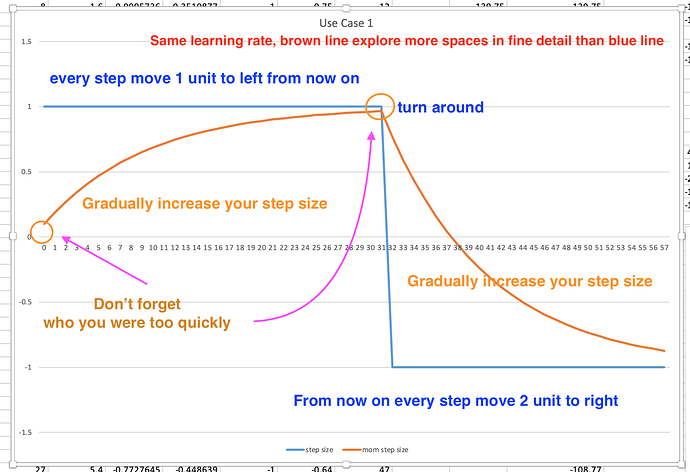
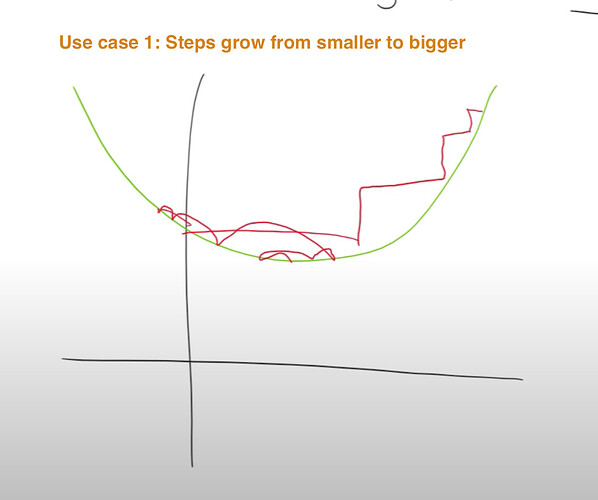
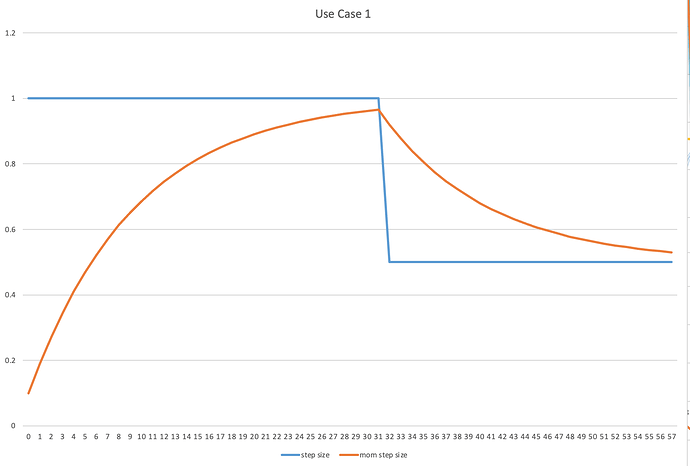
Use Case 1: when derivatives are not jumping big and back and forth
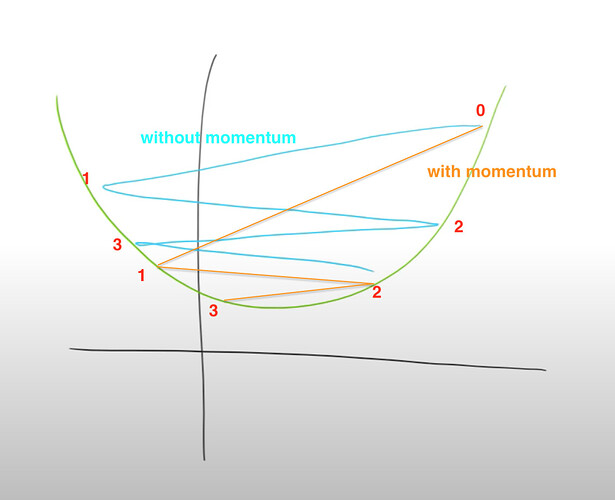
Momentum: remember where you were and don’t jump at a full change, only increase the change or step size gradually, so that you can explore more fine space having lower probability of stepping over the optimal (see the graph from the experiment). When your larger steps meet a derivative shows opposite direction with large value, then you are forced to turn around, still increase your steps gradually like above. (also see Jeremy’s drawing below)
Use case 2: when derivatives are jumping in large steps and back and forth
when derivatives are jumping in large steps and back and forth, it is not very efficient in finding the optimal. But when derivatives do jump back and forth, momentum can keep them jump in smaller steps so that you are closer to the optimal than without momentum. ( see the graph illustration below)
Questions
There is something which is confusing when Jeremy talked about use case 1:
“If you are here and your learning rate is too small, if you keep doing the same steps, then if you also add in the step you took last time, and then your steps are getting bigger and bigger aren’t they? Until eventually they go too far …”
This quote sounds like “the same steps” are too smaller but after applied momentum, they will become bigger and bigger. But this interpretation can’t be right. According to our experiment below, if the same steps are always 1 and also greater than the initial momentum step 0, then the increasing momentum steps can never be bigger than 1. Then if sudden the same steps are changed to 0.5 and remain on this value onward, then the step value produced by momentum will decrease but is always greater than 0.5. (If I am wrong here, could anyone help me get this straight? thanks)