Lesson 9 Discussion & Wiki (2019)

[brismith (Brian Smith)]

At around 58m in last nights video Jeremy goes though this in the 03_minibatch notebook. Might be earlier in the edited video when that appears.

[RawanSaifAldeen (Rawan Abdulsadig)]

So basically .backward() calculates the gradients, saves the values (or adds them to previously saved values) and gets rid of the chain of operations so the next operation chain starts clean, and .zero_grad() only manipulates those saved values. Makes sense.
Thank you Jeremy

[tanyaroosta]

It would be good to have a separate topic for it. I have no background in callbacks and would be great to see other people’s insights in a thread.

[jeremy (Jeremy Howard)]

@tanyaroosta

It would be good to have a separate topic for it

Please do feel free to create a topic about callbacks, or anything else you’re interested in!

[Mirodil]

Would it be a correct statement about initialization weights? We get faster covergans and better prediction with better initialization weights.

[KevinB (Kevin Bird)]

I was looking through the sqrt 5 notebook yesterday and I am wondering if this is something that should be refactored:

c = y_train.max()+1

to

c = torch.tensor(y_train.unique().numel())

This gives the same result although it takes a bit longer to run. The reason I think it would be better is that it could be transferred to different datasets or if not all of mnist is loaded and not all 10 numbers are represented, this could be off.

I submitted a pull request to change it, but just curious if anybody agrees or disagrees with it as a change.

And maybe since this is just an exploratory notebook, and you know you want c to be equal to 10, this isn’t even something to consider, but it just caught my attention when I was dissecting the magic.

EDIT: Jeremy responded to the pull request:

@Jeremy

There’s upsides and downsides to this approach - but we’re really just showing something that works for this one dataset here, and I’d rather keep it consistent with the video and keep it simple.

[Kaspar (Kaspar Lund)]

Really cool lecture jeremy - thx

[Pomo (Malcolm McLean)]

Thanks for replying. It’s not the logsumexp trick, but the softmax that’s problematic to my intuition. For example, for image segmentation with three classes, one pixel has activations -1,-2,-3. The pixel next door has activations -5,-6,-7. After exponentiating and scaling to add up to 1, the two pixels generate identical class probabilities. Therefore the same log probabilities and the same cross entropy loss.

What I’d like to understand intuitively is 1) what is the difference between these two pixels, and 2) how does it make sense that they contribute identically to the loss?

Also, as I’m writing this, wondering whether they contribute identically to the gradient as well.

Thanks for helping me think this through.

[tanyaroosta]

I created a separate topic for callbacks:

Callback discussion from lesson 9

I am creating a separate topic to discuss the callback. Here is the link to what callbacks are that was posted in lesson 9, to get us started. This is a wiki post, so please edit it to add any use resources you find.

[mediocrates (Justin Shih)]

It’s worth noting that mathematically, the two scenarios are the same – as far as the model is concerned – not only are the losses the same, the gradients are also the same (if I’ve done my math correctly):

\frac{\partial}{\partial x}\left(\frac{e^x}{e^x + e^y}\right) = \frac{e^xe^y}{(e^x+e^y)^2},

which is also invariant under translation by a constant. So there’s no difference to the model whether you have (x, y, z) or (x, y, z) + k.

But it sounds like you’re wondering whether (-5, -6) means that we don’t think it’s a cat or a dog, but that we’re slightly more confident that it’s a cat, and (-1, -2) means that we think that it’s a cat and we also think that it’s a dog, but we’re equally confident that it’s a cat. I don’t think that’s an unreasonable interpretation – could you come up with a test for that somehow?

If I had to pick, I would be inclined to not believe that interpretation, because the model only knows about cattiness in relation to dogginess, not cattiness in a vacuum.

[AlexisGallagher]

I think the YouTube title for this video may be incorrect. It says Lesson 8 when this is Lesson 9.

[Pomo (Malcolm McLean)]

But it sounds like you’re wondering whether (-5, -6) means that we don’t think it’s a cat or a dog, but that we’re slightly more confident that it’s a cat, and (-1, -2) means that we think that it’s a cat and we also think that it’s a dog, but we’re equally confident that it’s a cat. I don’t think that’s an unreasonable interpretation – could you come up with a test for that somehow?

That’s an interpretation I had not thought of, but it could be reasonable. Actually I have no problem with a difference of 1 anywhere on a log scale meaning the same ratio of probabilities.

What I wonder is whether (-1,-2) means there’s definitely something cat or dog like here, cat more likely than dog by a factor of e. While (-5,-6) means there’s nothing very cat or dog like here (it’s a spoon!) but the spoon looks more like a cat by the same ratio, according to the features the model has learned.

If that’s a correct interpretation, maybe in evaluation we should return “unknown” when the underlying activations are small. Maybe this softmaxing of small activations underlies some of the adversarial example problems.

[Chris_Palmer]

Thanks @PierreO - makes sense!

[jeremy (Jeremy Howard)]

@AlexisGallagher

I think the YouTube title for this video may be incorrect. It says Lesson 8 when this is Lesson 9.

Thanks fixed.

[jeremy (Jeremy Howard)]

@Pomo

What I wonder is whether (-1,-2) means there’s definitely something cat or dog like here, cat more likely than dog by a factor of e. While (-5,-6) means there’s nothing very cat or dog like here (it’s a spoon!) but the spoon looks more like a cat by the same ratio, according to the features the model has learned.

If that’s a correct interpretation, maybe in evaluation we should return “unknown” when the underlying activations are small. Maybe this softmaxing of small activations underlies some of the adversarial example problems.

Yes it’s a major problem with softmax. It’s overused as an activation function. It’s only suitable when you have exactly one object of your labeled classes present. We’ll talk about this next week.

[edwardeasling]

I have a quick question about the “02a_why_sqrt5” notebook.

In this notebook, we create a model with four Conv2d layers, using the default initialization method:

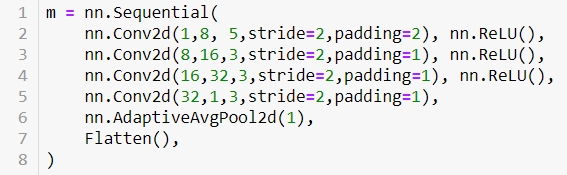
Then we re-initialize the weights in each layer with init.kaiming_uniform_:

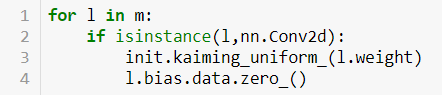
When you use init.kaiming_uniform_, it looks like it assumes a=0 by default. But shouldn’t we be setting a=1 for the final Conv2d layer, since there is no ReLU following it?

[supercurious (Vincent Tam)]

In the 02b_initializing notebook, the provided formula for standard deviation:

\sigma = \sqrt{(x_{0}-m)^{2} + (x_{1}-m)^{2} + \cdots + (x_{n-1}-m)^{2}}

is missing the mean of the squares. Should be:

\sigma = \sqrt{\frac{1}{n}\left[(x_{0}-m)^{2} + (x_{1}-m)^{2} + \cdots + (x_{n-1}-m)^{2}\right]}

Appreciate the intuition behind the “magic number for scaling” in Xavier and Kaiming init!

[sgugger]

Oh yes, I forgot the 1/n. If you want to make a PR to add it, that would be much appreciated!

[cqfd (Alan O'Donnell)]

Yeah, was about to say the same thing. The loss doesn’t care if you add a constant to all of the activations that get fed into the softmax, so I don’t think there’s any way for the model to learn what should be considered “large” or “small”. E.g. I want to say that two different initializations of the network could wind up working just as well, but one spits out activations like (-5, -6) while the other does (-1, -2).

If you want the model to be able to say that it’s not sure, you need to explicitly allow it to by including an extra category.

[supercurious (Vincent Tam)]

Happy to!