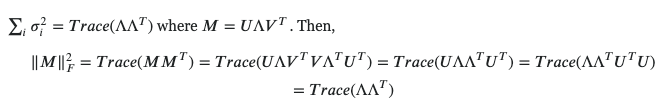Lesson 8: Frobenius Norm Alternate Equation Question

Part 2 (2019)
1

\|A\|_{\rm F} = \sqrt{\sum_{i=1}^m \sum_{j=1}^n |a_{ij}|^2} = \sqrt{\operatorname{trace}\left(A^* A\right)} = \sqrt{\sum_{i=1}^{\min\{m, n\}} \sigma_i^2(A)},

While I was studying lesson 8 again, I noticed that while trying to study the code and Implement a different equation of Frobenius Norm I come across an issue where the fastai’s version and the one I implemented does not come even close to equalling the same number. What did I do wrong?

Also while I’m here, i’m a bit curious what the \sigma^2 is supposed to be in the final implication of this equation

torch.manual_seed(7)
m = torch.randint(0,3,(3,3)).float() //[0., 1., 1.], [2., 1., 0.],, [2., 2., 1.]]

#Return The Frobenius Norm
def frobeniusNorm(T):
    return (T*T).trace().sqrt()

# Return Jeremy's Frobenius Norm
def fastaiFrobeniusNorm(T):
    return (T*T).sum().sqrt()

#returns (tensor(1.4142), tensor(4.))
frobeniusNorm(m), fastaiFrobeniusNorm(m)
1 Like
2

13%20PM
Screen Shot 2019-08-21 at 1.04.13 PM.png1094×687 49.9 KB

s, sigma is a diagonal matrix with non-negative real numbers on the diagonal. They are the singular values of matrix m when you take the svd of m.
[https://en.wikipedia.org/wiki/Singular_value_decomposition] (svd)
so for fastaiFrobeniusNorm it is elementwise (*)
and frobeniusNorm the svd way you need to do a matrix multiplication(@)

2 Likes
3

Thank you for reaching back and going beyond!
Last question, did i misread the wiki , because it did not tell me at all that i was supposed to take the transpose. It did on wolfromalpha though :grinning:.

4

I think that is an error(Not sure let me check ). This is the derivation-
16%20PM

Haha that is not an error the * is not multiplication it is the conjugate transpose. If you notice carefully the * is not in the centre of the line (to indicate multiplication) but in fact is slightly to the top. Would have been better to have it written as AA*.

6

alright. everything makes sense now! :blush:

7

The Frobenius norm of a matrix is the square root of the sum of the squares of its elements; it provides a rough measure of the “size” of the matrix.

Wikipedia gives three ways of expressing the Frobenius norm of a matrix whose elements are real numbers:

\|A\|_{\mathrm{F}}\equiv \sqrt{\sum_{i=1}^{m} \sum_{j=1}^{n}\left|a_{i j}\right|^{2}}=\sqrt{\operatorname{trace}\left(A^{T} A\right)}=\sqrt{\sum_{i=1}^{\min \{m, n\}} \sigma_{i}^{2}(A)}

Here, the superscript ^{T} refers to the transpose matrix, and the singular values \sigma_{i}(A) are the square roots of the eigenvalues of the matrix A A^T

The third expression is the square root of the sum of the eigenvalues of A A^T; although mathematically interesting, it’s not the best way to compute the Frobenius norm.

Let’s demonstrate the equality of the 1st and 2nd expressions. Suppose A is an n\times m matrix, i.e. A has n rows and m columns.

Then

A^{T} A is an m\times m matrix whose diagonal elements are

A_{j} \cdot A_{j}, where j runs from 1 to m, and

A_{j} \equiv (a_{1j}, ..., a_{nj}) is the jth column of A.

The diagonal elements of A^{T} A are evidently the set of dot products of each column of A with itself.

\operatorname{trace}\left(A^{T} A\right) is defined as the sum of the diagonal elements of A^{T} A,

which is just the sum of the squares of all the elements of A.

QED

It’s interesting to note that the order of the terms in the product of the matrix with its transpose doesn’t matter, giving rise to an alternate form for the Frobenius norm:

\operatorname{trace}\left(A^{T} A\right) = \operatorname{trace}\left(A A^{T} \right);

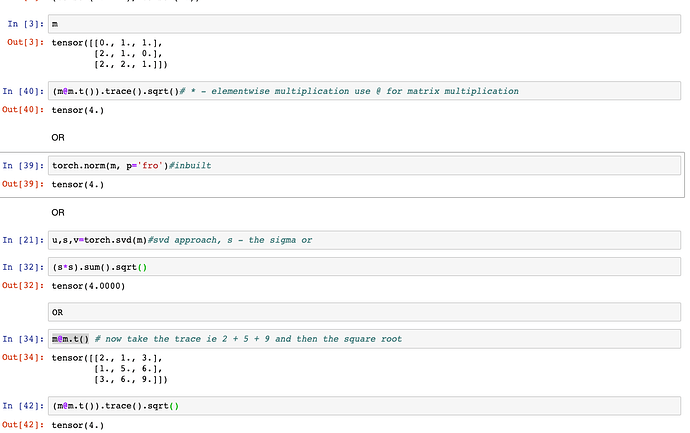
\operatorname{trace}\left( A^{T}A \right) is the sum of the m dot products of the n\times1 column vectors of A with themselves, while \operatorname{trace}\left(A A^{T} \right) is the sum of the n dot products of the m\times1 row vectors of A with themselves. The expressions are equivalent because each reduces to the sum of the squares of the elements of the matrix A. Their computational complexity is O(mn), which is lower than that of the singular value decomposition required to compute \sigma.