Does anyone know why we are not zeroing out the gradients after each epoch in this course notebook (Linear model and neural net from scratch | Kaggle)? This is something that is normally done during each mini-batch/step, which in this notebook - 1 step/mini-batch is one training epoch as there is only a single batch, and seems like a bug although it does not seem to negatively affect the loss and accuracy too much when training for 30 epochs, but I have noticed some other issues. Maybe it does not matter in this case because of the relatively small dataset size and relatively small number of epochs. I’m trying to figure out if this was done on purpose or is a bug.
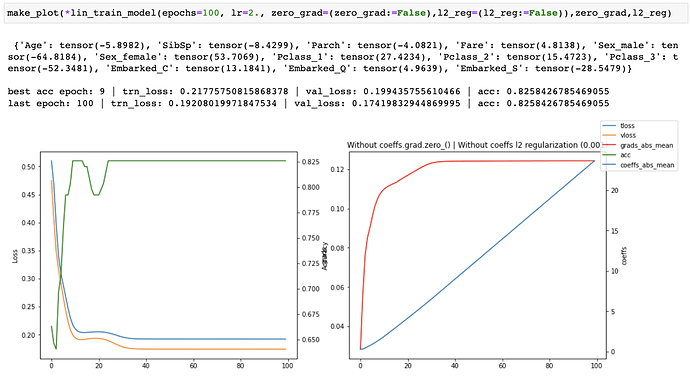
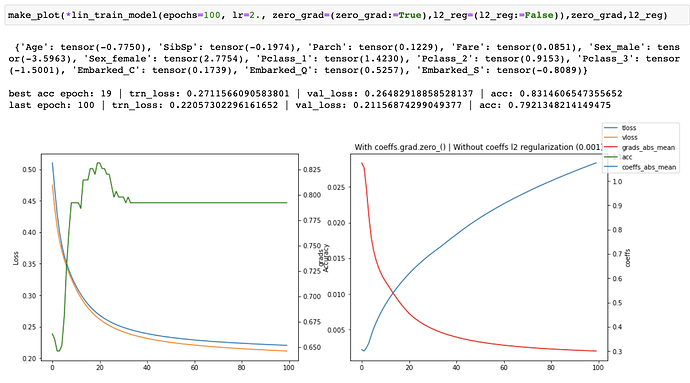
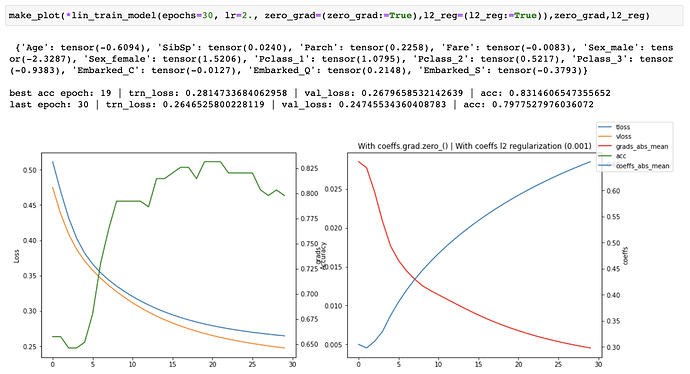
I ran a series of experiments on the linear model both with and without coeffs.grad.zero_(). When training for 30 epochs, I was able to achieve a slightly higher accuracy 0.831460 with coeffs.grad.zero_() at epoch 19 vs 0.825842 without it (matching the accuracy in the course notebook), but the losses were consistently worse and accuracy was worse at the original final epoch (30) as well.
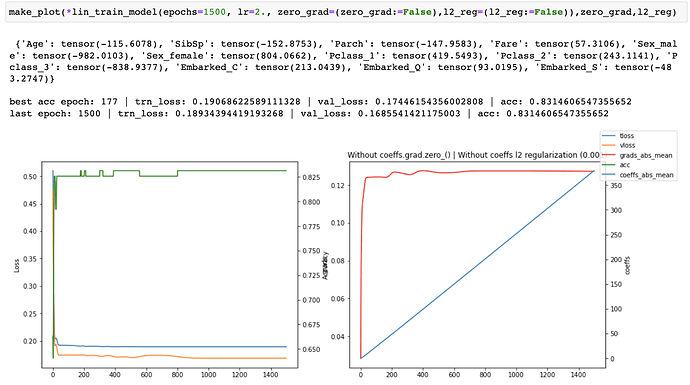
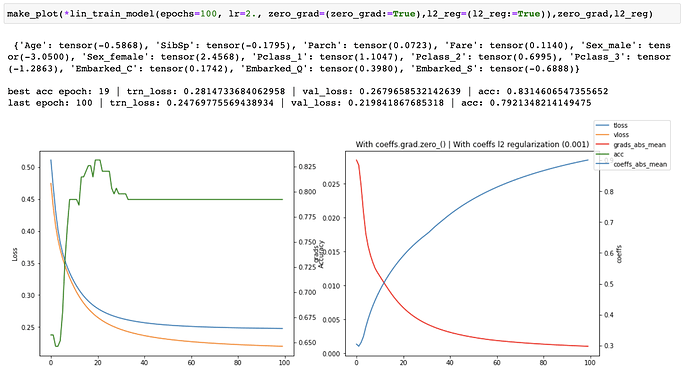
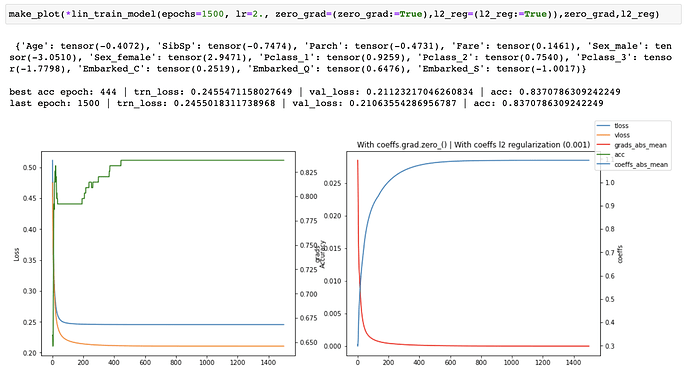
I then started tracking the losses, accuracy, gradients and coefficients and created plots of each one of them to see what was happening as training progressed. I ran both with and without coeffs.grad.zero_() for 30, 100 and 1500 epochs.
without coeffs.grad.zero_()
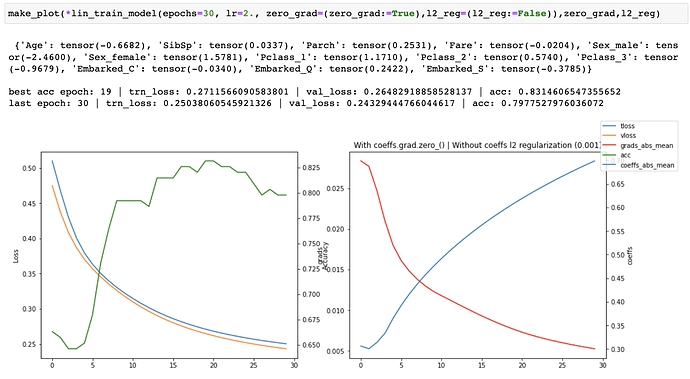
with
coeffs.grad.zero_()When running without zero_grad_ I noticed that the coefficients were growing linearly with the number of epochs which is not ideal. When running with zero_grad_ the coefficients were still continuously growing, but the graph of the coefficients looked like a log graph instead of a linear graph and the overall values were much lower which was much better. I then added a simple l2 regularization (ish) of the coefficients to the loss and ran some more experiments. This helped to prevent continuous growth of the coefficients.
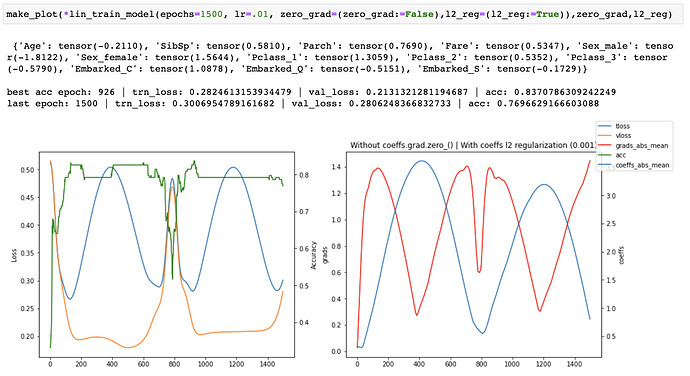
I then tried keeping the coefficient l2 reg and turning off zero_grad_ and that caused training to become unstable, even with a much lower learning rate. This happened consistently across a number of different runs with different hyperparameters, but I have only included the screenshot from the final run.
Finally, I recorded the coefficients across multiple runs with an increasing number of epochs, all without l2 reg. I observed that while the coefficients were continually growing, their relative values between one another was converging.
Code
trn_split, val_split = RandomSplitter(seed=SPLITTER_SEED)(t_indep)
len(trn_split), len(val_split)
trn_indeps, val_indeps, trn_deps, val_deps = t_indep[trn_split], t_indep[val_split], t_dep[trn_split], t_dep[val_split]
n_coeffs = t_indep.shape[1]
print('n_coeffs',n_coeffs)
def lin_init_coeffs():
torch.manual_seed(TORCH_SEED)
return (torch.rand(n_coeffs)-0.5).requires_grad_(True)
coeffs = lin_init_coeffs()
def lin_show_coeffs(coeffs): return dict(zip(indep_cols, coeffs.requires_grad_(False)))
def lin_update_coeffs(coeffs, lr=.01,zero_grad=True):
with torch.no_grad():
coeffs.sub_(coeffs.grad*lr)
if zero_grad: coeffs.grad.zero_()
def lin_calc_preds(coeffs, indeps):
return torch.sigmoid((indeps*coeffs).sum(axis=1))
def lin_calc_loss(preds, deps):
return (preds - deps).abs().mean()
def lin_calc_acc(coeffs):
with torch.no_grad():
preds = lin_calc_preds(coeffs, val_indeps)
ret = ((preds > 0.5) == val_deps.bool()).float().mean()
return ret
def lin_calc_epoch(coeffs, indeps, deps, lr=2.,zero_grad=True,l2_reg=True):
preds = lin_calc_preds(coeffs, indeps)
loss = lin_calc_loss(preds, deps)
if l2_reg: loss += (coeffs.square().sum()) * .001 #prevent unbounded growth of coeffs
# print(f'loss {loss:.3f};',end='')
loss.backward()
grads = coeffs.grad.data.clone().detach().abs().mean()
lin_update_coeffs(coeffs,lr,zero_grad=zero_grad)
with torch.no_grad():
val_preds = lin_calc_preds(coeffs, val_indeps)
val_loss = lin_calc_loss(val_preds, val_deps)
acc = lin_calc_acc(coeffs)
# print(f'acc: {acc:.4f};',end='')
return loss.detach(), val_loss.detach(), acc, grads, coeffs.clone().detach().abs().mean()
def lin_train_model(epochs=30, lr=2.,zero_grad=True,l2_reg=True):
trn_loss,val_loss,acc, grads, coeffs_track = [],[],[],[],[]
coeffs = lin_init_coeffs()
for e in range(epochs):
tl,vl,a,gr,c = lin_calc_epoch(coeffs,trn_indeps,trn_deps,lr,zero_grad=zero_grad,l2_reg=l2_reg)
trn_loss.append(tl);val_loss.append(vl);acc.append(a);grads.append(gr);coeffs_track.append(c)
print('\n',lin_show_coeffs(coeffs).__str__(),'\n')
return trn_loss, val_loss, acc, grads, coeffs_track
def make_plot(tl,vl,acc,grads,coeffs_track,zero_grad,l2_reg):
best_acc_epoch = np.argmax(acc)
print(f'best acc epoch: {best_acc_epoch} | trn_loss: {tl[best_acc_epoch]} | val_loss: {vl[best_acc_epoch]} | acc: {acc[best_acc_epoch]}')
print(f'last epoch: {len(acc)} | trn_loss: {tl[-1]} | val_loss: {vl[-1]} | acc: {acc[-1]}');xs = list(range(len(tl)))
fig, (ax1,ax3) = plt.subplots(ncols=2,figsize=(16,6));ax2 = ax1.twinx();ax4 = ax3.twinx(); ax1.set_ylabel('Loss');
ax2.set_ylabel('Accuracy');ax1.plot(xs,tl,label='tloss'); ax1.plot(xs,vl,label='vloss');ax4.plot(xs,coeffs_track,label='coeffs_abs_mean')
ax2.plot(xs,acc,label='acc',color='g');ax3.plot(xs, grads, label='grads_abs_mean',color='red');fig.legend();
ax3.set_ylabel('grads');ax4.set_ylabel('coeffs')
title = f"{'With' if zero_grad else 'Without'} coeffs.grad.zero_() | "
title += f"{'With' if l2_reg else 'Without'} coeffs l2 regularization (0.001)"
_ = plt.title(title)
#EXAMPLE RUN:
make_plot(*lin_train_model(epochs=30, lr=2., zero_grad=(zero_grad:=False),l2_reg=(l2_reg:=False)),zero_grad,l2_reg)
Overall this was an interesting set of experiments and utilizing a simple linear model made it easier to wrap my head around everything that was going on. The graphs really helped visualizing what was going on during training.
Sorry for the super-long post!
EDITS:
- Added a reference to the course notebook I am referring to.
- Clarified question - Is omitting zeroing grads after epochs done on purpose or is it a bug.
- Clarified zero_grad is typically done at the end of one mini-batch/step, not epoch, but in this case since there is only one batch, a batch and epoch are the same thing.
- Jeremy confirmed gradients should be zeroed after each epoch in the referenced course notebook and it has been updated to add in that functionality so this question will no longer make sense if you view the notebook I was referring to. Here is a link to the version before it was added so you see what I was referring to originally: Linear model and neural net from scratch | Kaggle . It’s pretty cool that Kaggle keeps notebook revisions. Thank you Jeremy for the confirmation!