I wanted to share a small insight I had. Jeremy might have explained this but, if so, I wasn’t paying attention and had to learn this painfully, through trial-and-error.
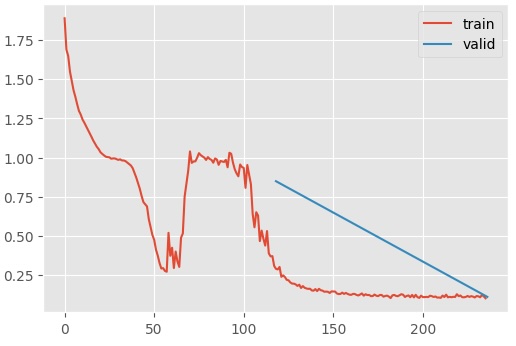
Notice that Jeremy doesn’t use Kaiming initialization when training the diffusion U-net. If you do so, the model converges on a loss of 1 for a while before it’s able to find a more optimal solution.
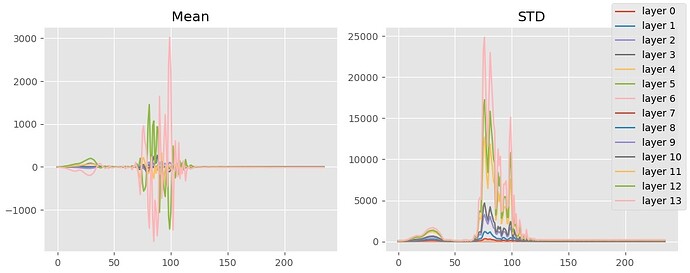
Plotting the summary statistics of the output of the resblocks, you’ll notice that this “phase shift” (is there a better word for this?) occurs when the means converge on 0. Before then, the means and standard deviations are all over the place.
I concluded that the model first has to learn a mechanism to compensate for extremely large activations before it can meaningfully fit to the epsilons. Why?
My insight arrived when I tried to the following: if you do not use Kaiming, then the loss/time curve is quite smooth.
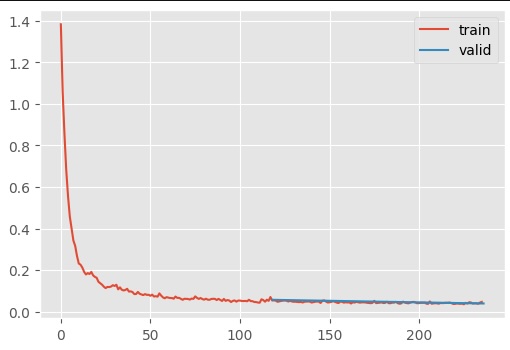
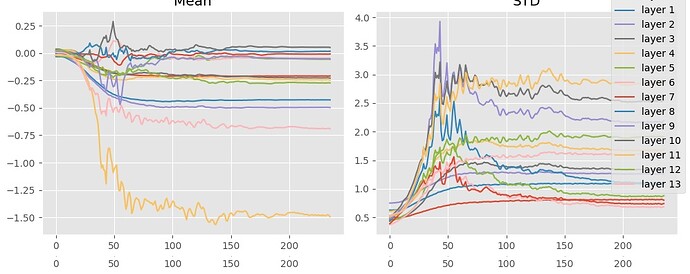
The summary statistics also look quite reasonable.
Why does Kaiming initialization result in this bizarre training dynamic? Keep in mind that Kaiming is designed to reduce to variance to 1 when the output of a neural network is expected to be only non-negatives, due to the ReLU activation function. However, a preactiviation res block does not apply ReLU to the residual link. In other words, we expect the output to have roughly unit-variance by default. Therefore, the default initialization is more appropriate to ensure that the activation magnitudes do not increase throughout forward propagation.