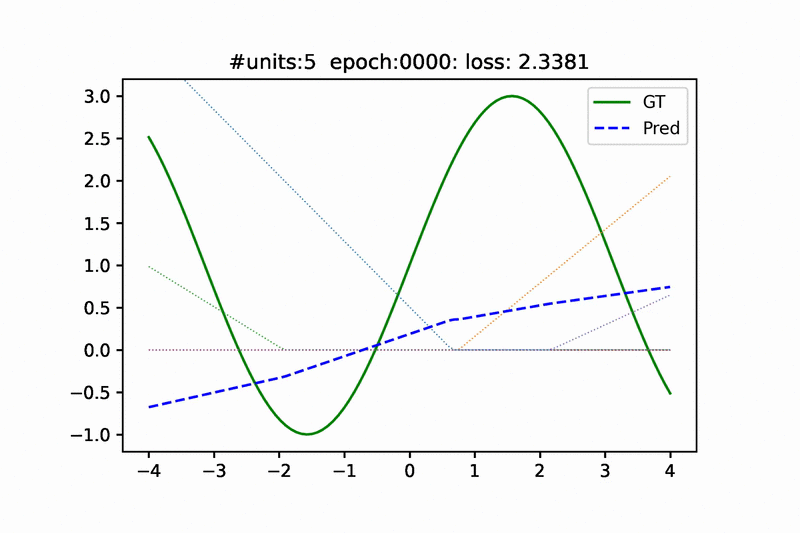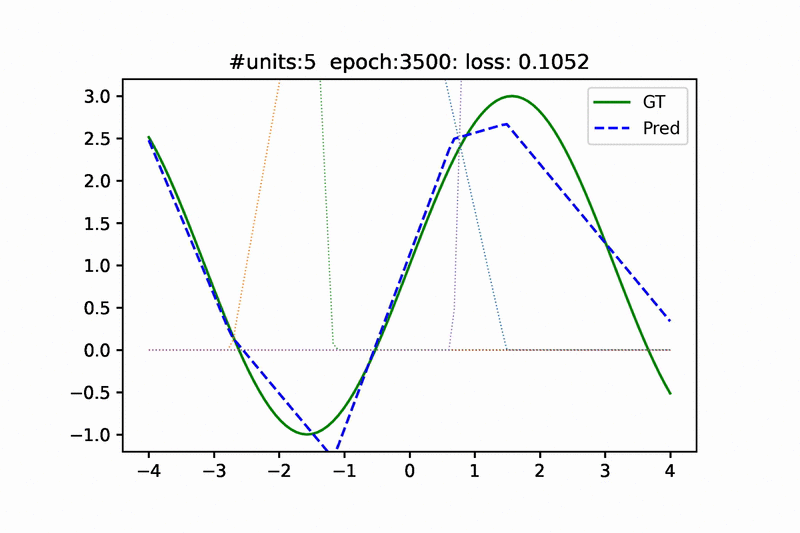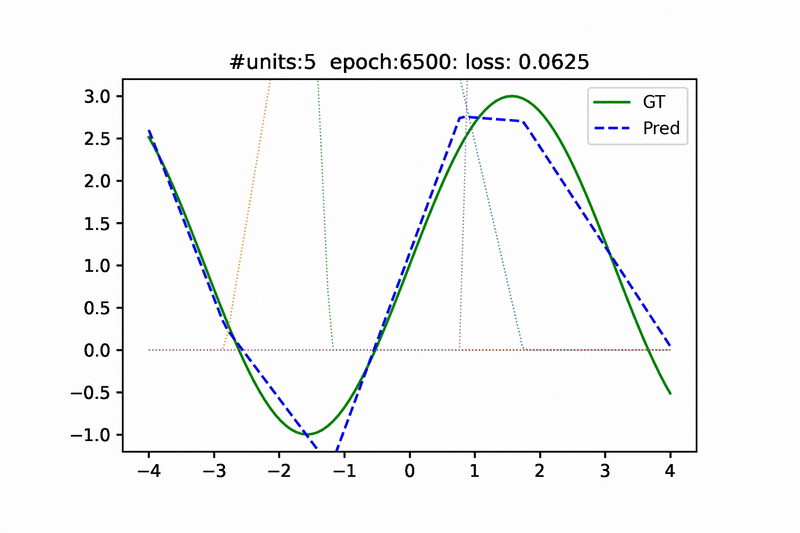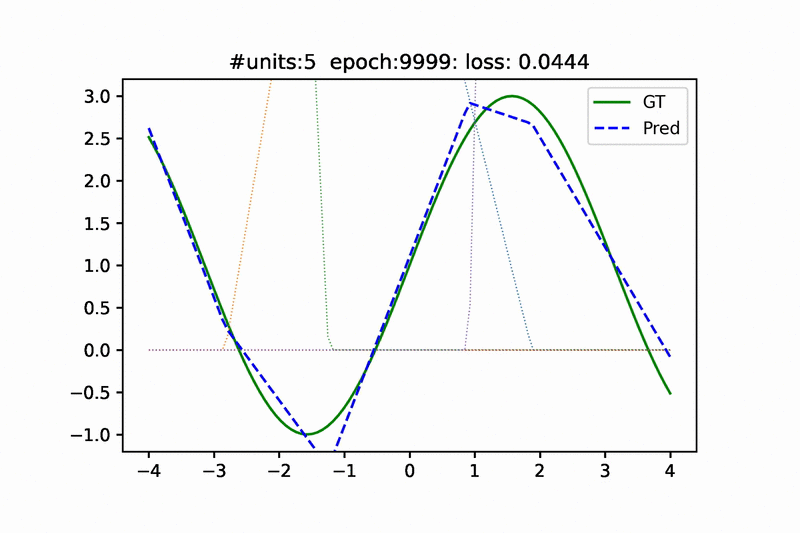
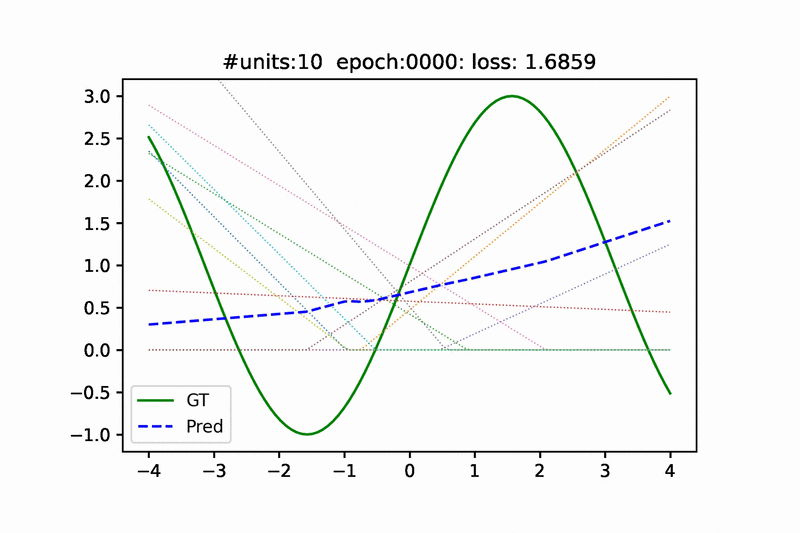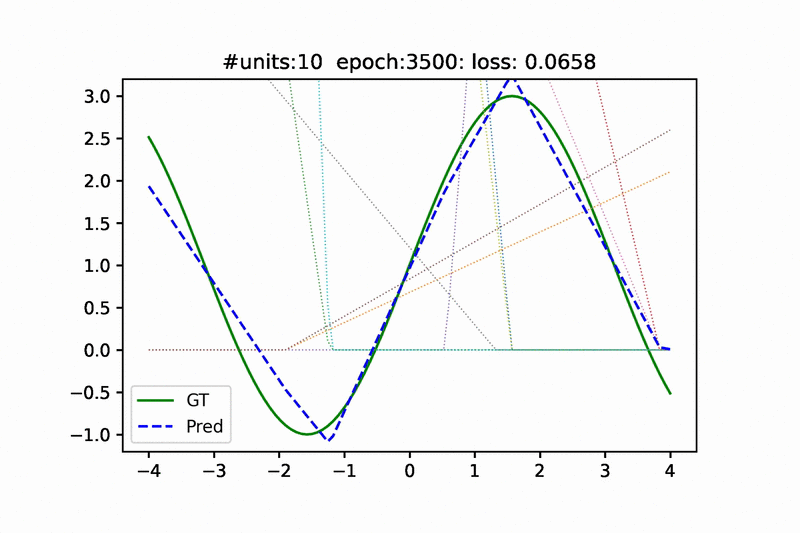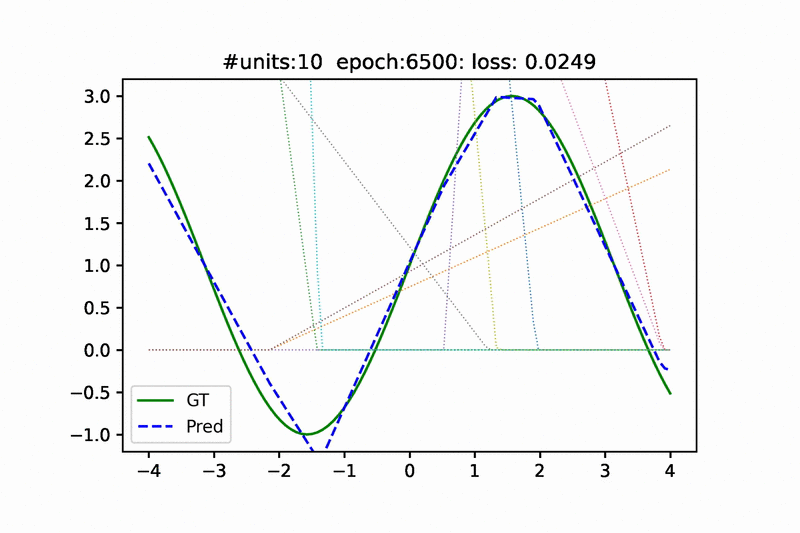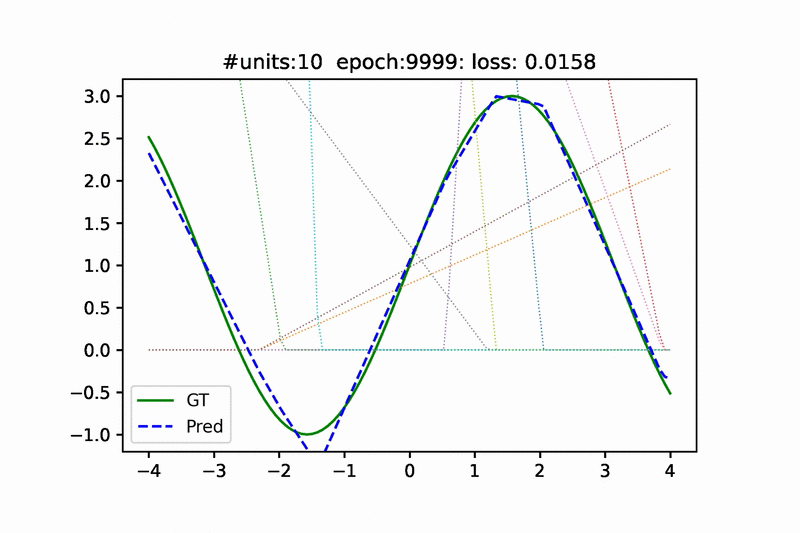
Hello,
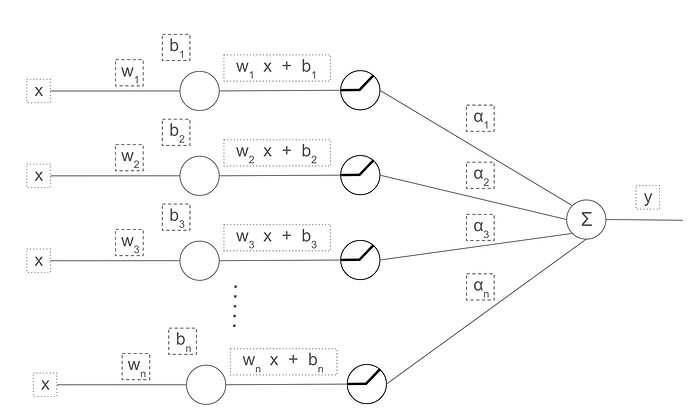
To understand this let us first set all the code we need, then we will take it execute it step by step.
Our building blocks are:
- the lin function:
def lin(x, w, b): return x@w + b
- the mse function:
def mse(output,target): return ((output.squeeze()-target)**2).mean()
and the classes: Mse(), ReLU(), Lin() and Model()
Now to create our model and compute backpropagation we run the following code:
model = Model(w1, b1, w2, b2)
what happens now?:
We are calling the Model constructor so if we look inside the object model we will find:
model.layers = [Lin(w1,b1),Relu(),Lin(w2,b2)]
model.loss = Mse()
Let’s name our layers L1, R, and L2 to make the explanation easier to follow.
so L1.w = w1, L1.b = b1, L2.w = w2 and L2.b = b2.
Now let’s execute the following line:
loss = model(x_train, y_train)
here we are using the model object as if it was a function, this will trigger the __call__ method, here is the code for it:
def __call__(self, x, targ):
for l in self.layers: x = l(x)
return self.loss(x, targ)
let’s execute it:
in our case x = x_train and targ = y_train
now let’s go through that for loop: for l in self.layers: x = l(x)
the contents of model.layers is [L1,R,L2]
so the first instruction will be: x = L1(x)
similarly here again we are using L1 as function so let’s go see what’s in its __call__ method and run it:
# Lin Call method
def __call__(self, inp):
self.inp = inp
self.out = lin(inp, self.w, self.b)
return self.out
so we are assigning inp to self.inp, in this case L1.inp = x_train and L1.out = lin(inp, w1,b1) = x_train @ w1 + b1.
The call method returns self.out so the new value of x will be x = L1.out.
The first iteration of the loop is done, next element is the layer R, so x = R(x)
# ReLU call method
def __call__(self, inp):
self.inp = inp
self.out = inp.clamp_min(0.)
return self.out
so now we have R.inp = L1.out R.out = relu(L1.inp) # basically equal to L1.inp when it's > 0, 0 otherwise.
Now the new value of x is x = relu(L1.inp)
The second iteration is done, next element is the layer L2, so x = L2(x)
now we have L2.inp = relu(L1.inp) and L2.out = relu(L1.inp) @ w2 + b2.
The new value of x is x = L2.out = relu(L1.inp) @ w2 + b2.
The for loop has ended. Let’s go to the next line of code 
return self.loss(x, targ)
We saw earlier that model.loss = Mse() so we are using the __call__ method of the Mse class:
# call method of the Mse class
def __call__(self, inp, targ):
self.inp, self.targ = inp, targ
self.out = mse(inp, targ)
return self.out
now we have mse.inp = x, mse.targ = targ and mse.out = mse(x, targ) = ((x.squeeze()-targ)**2).mean().
The method return mse.out so loss = mse.out.
Finally we get to the part which confused us both 
model.backward()
it calls the backward method of the Model class:
# backward method of the Model class
def backward(self):
self.loss.backward()
for l in reversed(self.layers): l.backward()
In the first line we have model.loss.backward() which is none other than the backward method of the Mse class. because remember that loss is an instance of the Mse class.
# backward method of Mse
def backward(self):
self.inp.g = 2 * (self.inp.squeeze() - self.targ).unsqueeze(-1) / self.inp.shape[0]
So here we compute mse.inp.g and we saw earlier that mse.ing = x so we are in fact computing x.g and it’s equal to x.g = 2 * (x.squeeze() - targ).unsqueeze(-1) / x.shape[0]
x as you know is the output of our MLP (multi level perceptron), and the gradient of the loss with respect to the output is stored in the output tensor i.e x.g. So that’s why it should be indeed inp.g and not out.g in the backward method of the Mse class.
Now in order to find out how backward of Lin get the out.g value let’s continue executing our code. We have have executed the first line now let’s run the for loop:
for l in reversed(self.layers): l.backward()
the first value of l is L2 (because we are going through the reversed list of layers)
so let’s run L2.backward()
# Lin backward
def backward(self):
self.inp.g = self.out.g @ self.w.t()
self.w.g = self.inp.t() @ self.out.g
self.b.g = self.out.g.sum(0)
We already know that:
L2.inp = relu(L1.inp)
L2.out = relu(L1.inp) @ w2 + b2 = x
so when we call L2.backward() this method will perform the following updates:
L2.inp.g = L2.out.g @ L2.w.t() # which is equivalent to L2.inp.g = x.g @ w2.t()
w2.g = L2.inp.t() @ L2.out.g
b2.g = L2.out.g.sum(0)
As you can see Lin knows automatically what out.g is, because when we ran model.loss.backward() we calculated it.
So now we have computed L2.inp.g (which is R.out.g) ,w2.g and b2.g.
The first iteration of the loop has ended, next l=R and we will run R.backward:
def backward(self): self.inp.g = (self.inp>0).float() * self.out.g
We know that R.inp = L1.out and R.out = relu(L1.inp)
The following updates will occur:
R.inp.g = (R.inp > 0).float() * R.out.g
Now we have computed R.inp.g (which is L1.out.g).
This iteration is done, next is l = L1 so we will call L1.backward().
We know that L1.inp = x_train and that L1.out = R.inp
So calling backward of L1 will give us the following updates:
L1.inp.g = L1.out.g @ w1.t() # which is equivalent to L1.inp.g = R.inp.g @ w1.t()
w1.g = L1.inp.t() @ L1.out.g
b1.g = L1.out.g.sum(0)
That’s it.
The main takeaway is that backpropagation strats at the end and compute the gradient of the loss and stores it in the output tensor of the neural network (which is the input tensor of the loss function, and that’s what’s confusing).
I really hope that it is clear to you now, have a good day!
![]()