Is the VBPR embedding just a Linear layer with bias?

Deep Learning
1

Hey,
Not sure this is the best place to ask but I have been looking at this Netflix presentation and they mention (read slide 15) VBPR as a way to tread cold start for recommender system.
So I read the paper and looked at some code and I can’t help to think that the embedding is really just a Linear layer with bias.
Taking for example this schema:
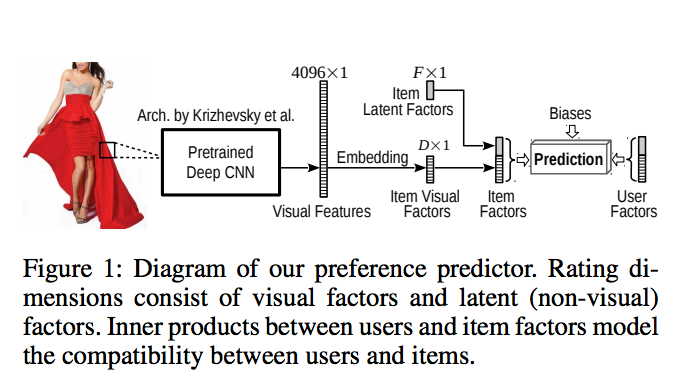
00%20PM
The embedding map the visual features from 4096 to K.
In the tensorflow code linked before it is achieve by doing this:

itemEmb_W = get_variable(type='W', shape=[model.imageFeatureDim, model.k2], mean=0, stddev=0.01, name='itemEmb_W')
itemEmb_b = get_variable(type='b', shape=[model.k2], mean=0, stddev=0.01, name='itemEmb_b')
visual_I_factor_pos = tf.sigmoid(tf.matmul(visual_I_matrix_pos, itemEmb_W) + itemEmb_b)

Where visual_I_matrix_pos is the 4096 vector of information of the image.
Can’t I just use something like torch.nn.Linear(4096,K)?
Please let me know if you need more clarification or if that’s not the right place to post it.

2

I worked w/ Prof McAuley during my grad work at UCSD and I am very familiar w/ the VBPR work (I implemented it in tensorflow).

It is a novel way to help the item-cold start problem in a domain where every item has an image, like Amazon.

Your question seems to be more general though: about embeddings being equivelent to a pytorch Linear layer. An embedding is just a matrix of weights where rows are interpreted as embedded items and columns are dimensionality of your representation. You can then select an item from the embedding by multiplying by a one hot encoded vector, so in other words, yes, it’s just like a pytorch linear layer which does the same thing.

1 Like