I feel like something is off with label smoothing. While the implementation is correct and agrees with the paper, my intuition suggests that the additional eps/N should not be added to the term for the correct class.
In the notebook for label smoothing we see the following explanation:
Another regularization technique that’s often used is label smoothing. It’s designed to make the model a little bit less certain of it’s decision by changing a little bit its target: instead of wanting to predict 1 for the correct class and 0 for all the others, we ask it to predict 1-ε for the correct class and ε for all the others, with ε a (small) positive number and N the number of classes. This can be written as:
loss = (1-ε) ce(i) + ε \sum ce(j) / N
where ce(x) is cross-entropy of x (i.e. -\log(p_{x})), and i is the correct class.
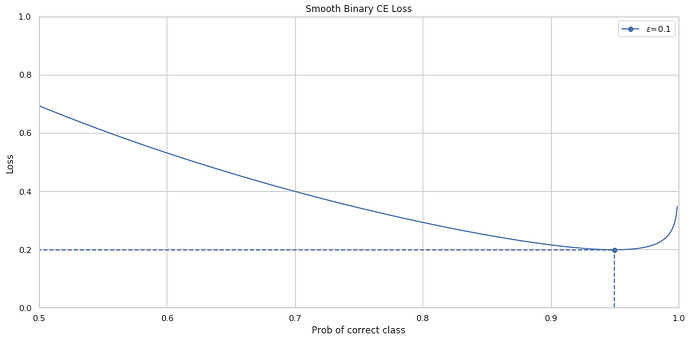
However, it turns out that the second sum is over the entire class list. I.e. , we never take special care to ignore the correct class. Thus, the coefficient for ce(i) becomes (1-ε + \frac{\epsilon}{N}).
This pushes the minumum of the function further to the right. For example, in the binary case with eps=0.1, if we use the original formula the minumum would be found at x=0.95 instead of x=0.9.
 )
)