In 04_mnist_basics：Why "bias" is not for every independent pixel

Part 1 (2020)
1

As previous paragraph of this chapter said, "we need an (initially random) weight for every pixel ", but why and why is possible to use one same bias for all pixels(multiplied by its weights and sum up them) in one image ?

bias = init_params(1)

(train_x[0]*weights.T).sum() + bias

As I print, shape of bias is Size 1.

Why not :

bias = init_params(28*28)

(train_x[0]*weights.T + bias).sum()

Thanks

2

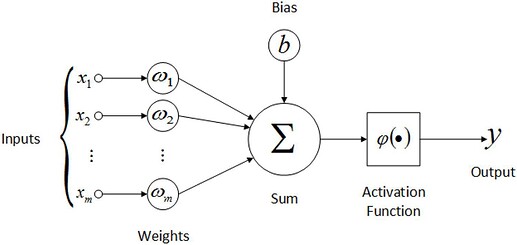
In MNIST at that point, we were modelling with just one Neuron:

one neuron
one neuron1400×664 65.3 KB

In the case of one neuron, we always assign every input a weight associated with it and that’s why we need a weight for every pixel. Also, for one neuron, we have one bias as shown in the image, to offset the matrix multiplication of the weights and inputs (for the cases where the multiplication produces a zero just as Jeremy said in the Lecture).

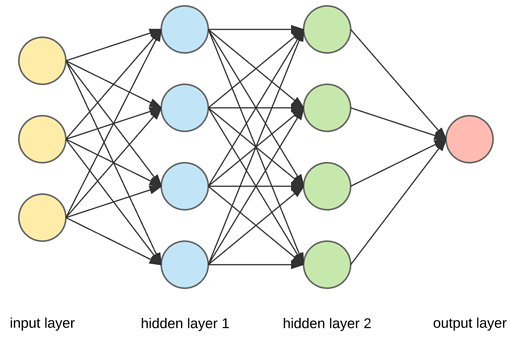
But in future, you are going to be modelling with layers that have more than one neuron:

multiple neurons
multiple neurons1318×862 34.3 KB

In the case of the above image, lets focus on Hidden Layer 1. (in blue). We have 4 Neurons, so what does this mean?

For each Neuron, we are going to have:

  • Three weights for each of the inputs (We have three inputs in the above example)
  • One bias

Hope this clarifies your question

3

I think the intuition is something like this:

The Bias is to handle the general characteristic of all the pixels
(i.e. in the case where the model handles images which are generally darker.)
or
when you normalize the weights to mean = 0, sd = 1, the average can be offset using the bias term.

1 Like
4

Thanks Jim for greate answer, the first image for one neuron exactly explained the MNIST at that point And I think @meanpenguin 's explaination also make sense:

The Bias is to handle the general characteristic of all the pixels(i.e. in the case where the model handles images which are generally darker.)

And some blog explained “Biologically, the neuron will be excited only when the input current in the nerve cell is greater than a certain critical value. And the certain value is actually the bias.”

w1*x1 + w2*x2 + w3 *x3 >= t

The above inequation equivalent to ：

w1*x1 + w2*x2 + w3 *x3  + b >= 0

I think

bias = init_params(1)

(train_x[0]*weights.T).sum() + bias

and

bias = init_params(28*28)
(train_x[0]*weights.T + bias).sum()

has almost the same meaning: bias = b0 + b1 + b2 + b3 +...
but the second bias(sum of a vector) has an inappropriate value range.

1 Like
5

These two do make sense! @BusyFox @meanpenguin
Thank you both for the extra info