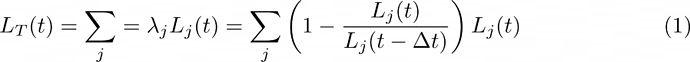Loss (Function) Finder?
Hey folks. Not sure if this is crazy or who might have already tried it, but here’s an idea that occurred to me…
Purpose
For well-studied problems (e.g., image classification), the choice of loss function may be obvious or mundane. But for new problems, it may not always be obvious which loss function (or combination of loss functions) would work the best. Given automated precedents such as grid search to try out different hyperparameters, Neural Architecture Search (NAS) to try out different architectures and activations, and FastAI’s LRFinder that suggests values for the learning rate, can we create a recommendation engine for which (combination of) loss function(s) are best suited for a given task? For example, Christian Steinmetz’s micro-TCN work recently blew away my SignalTrain model’s results, not only because of architecture changes but also due to a different (better) choice of loss function. If loss-suggestion were to be automated…who knows?
Basic Idea
Given a list of loss functions (e.g. losses=[mse, mae, log_cosh, delta_stft, wasserstein,...]) , see which one decreases by the greatest percentage over a given number of epochs during training.
I can conceive this operating in one of two different modes.
1. “Static Setup” Mode
The would be the first, simplest thing to try. Similar to FastAI’s LRFinder: Starting from the same initial state each time, we loop through a list of loss functions (i.e., for loss in losses:) and run a short training loop for each, making note of the percentage change in the value of the loss function.
(Question: Would it even be meaningful to try to compare log-loss type values with non-logarithmic ones in this way? I don’t know.)
Then the “winning” loss function is recommended to the user, who then starts their “real” training loop using only that loss function for computing gradients. (They may use another function for monitoring.)
2. “Dynamic Hydra” Mode
All loss functions L_j are evaluated concurrently at epoch t (thus denoted as L_j(t)) and their results combined into a total loss function L_T via a weighted sum in which each weight \lambda_j is given by the fractional change over some number \Delta t of recent epochs, something like:
$$ L_T(t) = \sum_j = \lambda_j L_j(t) = \sum_j \left( 1 - {L_j(t)\over L_j(t-\Delta t)}\right) L_j(t)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) $$
where time t is measured in epochs, and previous values L_j(t-\Delta t) are treated as constant numerical vectors, detached from network graphs and autograd calculations.
This could be run at all epochs during extended training, and might even dynamically adjust which loss function is dominant at different points during training. It also would likely be slow as molasses and may exceed GPU VRAM. To make backpropagation faster, perhaps \lambda_j's that have values smaller than some threshold could be set to zero.
Note that expression for \lambda_j in equation (1) is simplistic, and one might do better to use some kind of “(average) decay rate” expression for \lambda_j. Same basic idea though.
More Questions
-
Who has already tried something like this (‘this’ being the general idea, not just my ideas of mode 1 or 2)? Given 30+ years of people doing ML,…? Answer: Maybe this NIPS 2018 paper…ish…kinda? otherwise Google’s not helping me find anything similar.
-
If no one, is that because it’s a bad idea?
-
Who might have the inclination (besided me) and ability (not me, but learning) to maybe try to implement this, e.g. with fastaiv2? (maybe @muellerzr?) I can work on it just…not fluent with fastaiv2.
-
If it’s new and turns out to be useful,…where to go next?
-
Some loss functions kind of “plateau” at first before they really “take off” decreasing. Would Mode 1 not-recommend them? A: Probably would not recommend them, because maybe some other loss function would start decreasing immediately, and might be better anyway.
-
You realize that equation (1) is just the sum of all the loss functions, minus some weirdly-weighted sum of squares of all the loss functions? A: Yea, is that…bad?
Thanks for reading. I welcome your thoughts.