How to vectorize gradient calculation for convolutional neural nets?

Part 1 (2017)
1

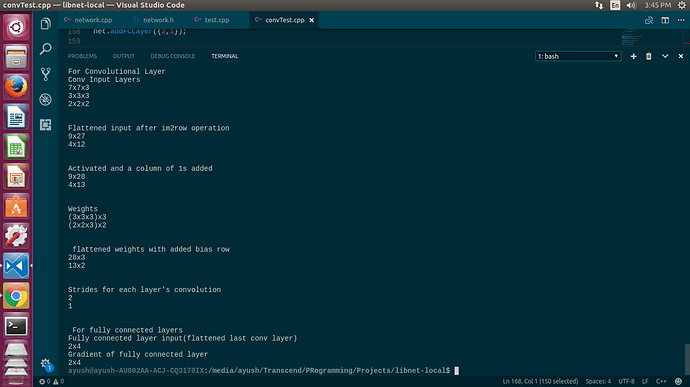
After trying out some libraries, I started to implement neural net from scratch. I have successfully implemented the fully connected network but I am stuck in gradient calculation for the convolutional layers. Here is a screenshot containing the architecture of the network. Please read the explanation regarding the screenshot to understand the details .

Screenshot from 2017-09-17 15-45-13.png1366×768 141 KB

Conv Input Layers
The first convolutional layer is the input, the second layer is the result of convolution on first layer and the third layer is the resultant of second layer which is flattened and used as fully connected layer.
Flattened Input layer
resultant after applying im2row(similar to im2col but transposed) operation to flatten and vectorize the 3D convolution calculation.
Weights
It represents the filters used for convolution. There ‘n’ are 3D filters. So the dimension is of the form (axbxc)xn
Strides
it represents the stride used for convolution operation in each layer. The first layer uses 2 strides and thus the resultant layer(i.e. the 2nd layer) is of dimension mxmx3 , where m=(7-3)/2 +1 = 3.
Next, the last layer is flattened and converted to fully connected layer and its gradient(dX) will be of the same dimension.
But I don’t know how to vectorize the gradient the gradient calculation for conv layer. Theoretically the gradient of a layer is the convolution between its weights and gradient of next layer but to implement that, the flattened layers and filters must again be converted to 3D and then convolved. I have read about vectorized implementation of gradients but I just can’t figure it out. So considering that I have already calculated the gradient of fully connected layer proceeding the last conv Layer, how can I calculate the gradient for the conv layer with actually using convolution again ?

2

I don’t recall much of that and also am not sure your description is really clear of what you are missing, but maybe still will be able to help.

I think what you are missing is the fact that you need to store all the activations along the forward pass. You then backpropagate the error and use the stored values to calculate the derivative. If you are using a max pooling layer, much of the work cannot be vectorized unless you store the values in some really smart way that I am not aware of.

And I am guessing that the same thing goes for actually the weights used for the convolutions. From what I recall, you will literally have to look at each and every window and then sum everything up.

This is my recollection and it can be faulty for which I apologize if that is the case. Maybe some of it will be helpful to you though.

I however at one point implemented a CNN from scratch like you are attempting and you can find the code here. If you hit a wall the code there definitely has an answer but I am not sure how easy it will be to read.

3

If you do the convolution but with the weights flipped horizontally and vertically, this is mathematically equivalent to doing a backward pass in the way you described.

Here is some Python + numpy code that shows this works: https://gist.github.com/hollance/c3762f3ae59238c74b98a0ff335cd30a

1 Like
4

Yeah trying to understand someone else’s code has always been difficult for me but nevertheless I’ll give it a shot.

5

Thank you very much for sharing this with me :slight_smile: This is great to know :slight_smile: