Dear all,
this is my first question on FastAI and I hope somebody can help me with this.
My question is about finding best model-size without overfitting, when using data-augmentation:
I am training a U-Net model (a fully convolutional neural network) for semantic segmentation. I use data-augmentation during training in the following way:
- I cut random crops from each training images.
- Each training image is seen once during an epoch with a random-crop selected. So: one random-crop per image per epoch.
I am now trying to determine best model-size in the sense, that the model should not overfit, but validation score is best possible.
It is my understanding, that this is usually achieved by varying/increasing model-size until training and validation curves start to diverge, which indicates that the model is overfitting.
However, as I am seeing now with data-augmentation things are not as clear-cut anymore. For instance consider the following two models:
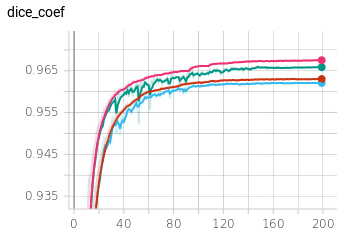
legend:
red+blue: training+validation (respectively) for model1 with size ~120000 parameters
pink+green: training+validation (respectively) for model2 with size ~460000 parameters
The difference between the two models, is that I have doubled the number of conv-layers in the first U-Net block from one to the other (due to U-Net topology this increases overall parameters by a factor ~4x).
For model2 training and validation diverge more than for the model1. However, validation-performance still goes up as well.
Now, if train model1 (the smaller model) without any augmentation (I always take the same crop for each image) I get this (Note: I used dice-loss here, whereas I used weight binary cross-entropy above - so the absolute values are not directly comparable):
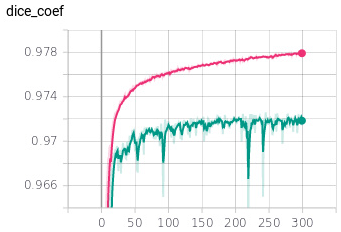
Now, this is clearly overfitting, I would say.
I therefore deduce, that the augmentation is causing the “uncertainty” about when the model is overfitting in the cases above. At the same time, I realize, that the whole aim of augmentation is precisely to reduce overfitting.
So this brings me to my question:
How do I determine that I am overfitting, when I am using data-augmentation? Are there any guidelines/rules-of-thumb?
Here I am using just random cropping, but I can try (and have) other, additional methods of augmentation. And those make the decision even harder.
Possible answer:
One option that comes to mind for defining “overfitting”, would be to say:
“We are overfitting, once the validation score does does not increase anymore with increasing model size.” Would this make sense?
Bonus question:
Is there an issue with my augmentation method?
To expand: currently, the model will “see” a different crop of a given image in each epoch (once per image). Alternatively, I could instead “show” it multiple crops for each image (so that in total the whole image is included) and keep those crops the same across all epochs. Would this be better?
I see the following advantages:
- This would probably remove the issue with determining overfitting, since it removes the randomness.
- Overall, the model would see more data to train on (in my case probably a factor 2x).
Is there a rule of thumb for doing this?