Help me understand Lesson 10 (Part 2)! :)

Part 2 (2019)
21

Not Radek :slight_smile: , but you can consider a 2x2 kernel

a b
c d

and a 3x3 kernel

a b 0
c d 0
0 0 0

They both do the same thing to your input! But then, as you start substituting the zeros in the 3x3 with other weights you can see how the 3x3 can be more general in the transformation it applies to the inputs!

For serial applications (e.g. 2 2x2 kernels vs 1 3x3 kernel) the argument is slightly trickier (and totally possible only without non-linearities involved) but we need to introduce the input x in the equation to be completely rigorous (I might write it up later tonight), but in synthesis you can still see that the second 2x2 kernel will introduce 4 other parameters, so the 3x3 still “wins” by one free parameter!

1 Like
22

That is a very nice observation :slight_smile:

My assumption is that people have experimented with various kernel sizes and that 3x3 turned out to be the best, at least on Imagenet and within the context of modern architectures.

23

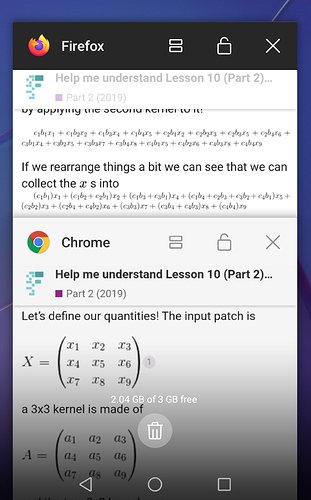
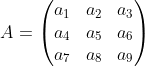
Let’s define our quantities! The input patch is

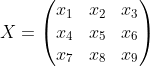
a 3x3 kernel is made of

and the two 2x2 kernels are

Now, let’s apply the 3x3 convolution to the input, the result is

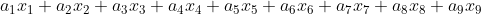
When instead we apply the 2x2 convolution in serie, we get first

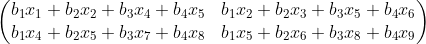
by applying the first kernel to the input and then

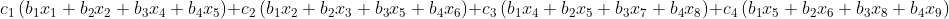
by applying the second kernel to it!

If we rearrange things a bit we can see that we can collect the x s into

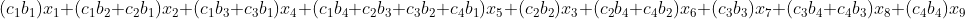
and so this is where we compare this result with the initial application of the 3x3 to the inputs (recall that it was this below)

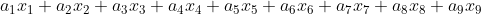
If we equate the two results we can see that for them to be equivalent we must have

but you can verify easily that when you try to solve this wrt to the kernel A (considering all of B abc C as given), this is trivially a system of 9 equations in 9 unknowns. I’ve laid out all you need to find the values of A!

(In layman terms, the 3x3 convolution can exactly reproduce the result of the two 2x2 convolutions if we do not take the non-linearities into account)

The problem comes from when you try to solve it the other way around, wrt to B and C! Unless we restrict some values of A, exactly one to be precise, this is a system of 9 equations in 8 (!!!) unnknowns, the values b_1, ... b_4, c_1, ... c_4, so the system has no solution!

Again, informally speaking this means that (non-linearity notwithstanding) the two 2x2 kernel cannot in general reproduce exaclty the result of a single 3x3 convolution!

The same of course apply to 5x5 versus two 3x3 kernels though, and we know that in practice often we get satisfactory results as well, but this is how you prove “formally” that a single bigger kernel is in general more expressive.

I hope that clear! :slight_smile:

EDIT: argh! equations are not rendered! Give me a sec while I work on a solution! :stuck_out_tongue:
EDIT2: saved? yes! Thanks codecogs

2 Likes
24

This is extremely interesting. I just finished the experiments on this and the results are spot on on what you just described. You can find the code here.

I run this experiment under the imagewoof dataset, the base accuracy I get by running the 3x3 convs is 0.65.

I first tried to just replace all 3x3 convs with 2x2 convs, the accuracy (not surprisingly) went down to 0.60.

Next step was to replace all 3x3 convs with two 2x2 convs having a non-linearity after every conv. Got a result close to 0.60 again.

For the final step, I replaced all 3x3 convs with two 2x2 convs, but only the second 2x2 conv had a activation, and then… Exactly 0.65 accuracy, exactly on point with:

Wow, this is incredible… Very very good work @marco_b

2 Likes
25

Thanks for running the experiments!

I’m glad some mathematical intuition still holds in this field ! :rofl:

2 Likes
26

Au contraire… The 3x3 loses by one free parameter. A sequence of two consecutive 2x2 convolutions can encode the spatial dependence within a 3x3 receptive field with only eight parameters, while a 3x3 convolution needs nine parameters to do the same job!

27

Sorry, the math did not render ^{\dagger} well on my Windows 10 machine running Firefox or on my Android.

But I do understand what you did, and it’s quite a nice demonstration (Math is beautiful!) The bottom line is that the eight parameters in the two 2x2 filters can be determined in terms of the nine parameters in the 3x3 filter (which yields an overdetermined system of equations), but the nine parameters of the 3x3 filter cannot be recovered in terms of the eight parameters of the two 2x2 filters (which yields an underdetermined system of equations).

More importantly, the result of @lgvaz’ excellent work comparing implementations of the two systems confirms the intuition that two 2x2 convolutions in series does the same job as the 3x3 convolution, but with 11% less memory required. This is essentially the point I was making to @radek

^{\dagger} You might try typesetting the latex equations directly into the message, i.e. not using a 3rd party app like codecogs.

For example, the following code
$T = \frac{T_0}{\sqrt{1-\frac{v^2}{c^2}}}$,

produces the following output (when you strip off the enclosing ``)
T = \frac{T_0}{\sqrt{1-\frac{v^2}{c^2}}}

There are many latex cheatsheets online that’ll get you up and running quickly. Here’s one.

1 Like
28

Interestingly enough doing two 2x2 convolutions in series takes more time to train.

1 Like
29

Ah yes this is what I’d expected in my comments to @radek. The 9 parameters of the 3x3 conv are solved in parallel on the GPU but a serial application of 2x2 convs presents a bottleneck and slows things down (by how much, incidentally?)

1 Like
30

3x3 is taking on avg 56s on my gpu, while 2x2 71s. So 26% slower

1 Like
31

So perhaps that’s why there isn’t widespread use of sequences of 2x2 convs?

32

Great tread!
I doing some experiments with resnet / xresnet, tryng better understend it. Refactor it a lot, have some interesting thougts, and then Radek start it!
I tried modify resnet and find best results (with woof) is when act_fn before Bn. Same with stem, and best result when in stem bn after maxpool.
Then i take stem from xresnet, but results not so good, Better with xresnet stem(3x3) with relu before bn, and last bn after maxpoool - it so good as base 7x7 conv, but non better,
Will check on long runs.

33

That’s what I did at first, but the subset of LaTeX that works on the Markdown implementation of this forums is apparently not enough to render my equations, that’s why I had to switch to codecogs. They’re simple GIF now, so they should render on any device … maybe you looked at the post before I edited and switched to the external tool?

By the way, it’s not like codecogs is a speech/handwriting recognition app, I still had to type those in there so I’m not sure what you mean by suggesting a LaTeX Cheatsheet :sweat_smile:

Back on topic,

The same could be said for the two 3x3 convs versus a 5x5 conv as well though. Most likely a combination of reasons…

I think point 2 is probably “solved” by now, I still don’t understand point 1, aka “you’re just shuffling the numbers” but If not proven wrong I’ll just assume that what he meant was similar to what I expressed here

so in the end we do agree even on this topic, just expressed in a way that made it hard for me to rally see it!

34

The equations still do not render in Firefox, either on Android or Windows 10 64-bit. I also checked the Chrome browser on Android, with the same result.

35

They render fine for me both on desktop and Android

Screenshot_20191120-101310
Screenshot_20191120-101310.jpg1080×1731 267 KB

They are now embedded images, there’s no reason other that weird / overaggressive adblocker or similar that they would not render … they’re GIFs! I’ve send you a PM since this is probably going too off-topic otherwise :slight_smile: