Hi everybody,
I’m here asking for some help about my first simple model from scratch.
I’m studying the version of the book I’ve recently bought on Amazon in kindle format. I’m not sure it is the last version of the book, because the chapter 4 is the same of the lesson 4 of the 2020 video course (not 2022 the one) but anyway, the book for me is good as it is, so I’m studying on it.
Currently I’m studying the chapter 4 and I’m trying to make all the stuff explained in the on my own as well, so now I’m creating my first simple model to work on the MNIST Simplified dataset, and I’m at the phase where I’m trying to do the training process manually, without using the Optimizer and the .fit() method.
There is not a specific problem that I’m facing, just the metrics I got are wired, and I’m quite sure something strange is happening, but I’m not able to figure out what exactly.
I’ll try to explain it better with some code and results.
I’ve defined a simple linear function
def linear1(x): return x@w + b
Then I’ve created a method call get_prediction which call the linear function and apply the sigmoid to it, in order to get a result from 0 to 1
def get_predictions(x):
return linear1(x).sigmoid()
Then I’ve defined the loss function
def mnist_loss(predictions, targets):
return torch.where(targets==1, 1-predictions, predictions).mean()
Then after creating the DataLoader and so on, I’ve created a function to calculate the predictions, calculate the loss and calculate the gradient
def preds_loss_grad_on_single_batch(xb, yb, model):
preds = model(xb)
loss = mnist_loss(preds, yb)
loss.backward()
Then I’ve create a function to train a single epoch (train_dl is the train data loader)
def train_epoch(model, lr, params):
for xb, yb in train_dl:
preds_loss_grad_on_single_batch(xb, yb, model)
for p in params:
p.data -= p.grad*lr
p.grad.zero_() # equivlente a p.grad = None
And at the end I’ve trained the model for some epochs and printed some output (lr is the same used on the book for this example)
CODE:
w = params_initializator( (28*28, 1) )
b = params_initializator(1)
params = w, b
lr = 1
epochs = 20
print("start training for " +str(epochs) + " epochs")
print("===")
for i in range(epochs):
loss = mnist_loss( get_predictions(train_x), train_y )
valid = validate_epoch(get_predictions)
print("[" + str(i) +"] Loss: " + str(loss.data.item()))
print("Validation: " + str(valid) )
print("-")
train_epoch(get_predictions, lr, params)
print("===")
print("end of training")
loss = mnist_loss( get_predictions(train_x), train_y )
print("loss afeter training: " + str(loss.data.item()))
OUTPUT:
start training for 20 epochs
===
[0] Loss: 0.6285527944564819
Validation: 0.3831
-
[1] Loss: 0.018473109230399132
Validation: 0.9755
-
[2] Loss: 0.01681487448513508
Validation: 0.974
-
[3] Loss: 0.013208670541644096
Validation: 0.9775
-
[4] Loss: 0.014201736077666283
Validation: 0.9814
-
[5] Loss: 0.011925823986530304
Validation: 0.9809
-
[6] Loss: 0.010863254778087139
Validation: 0.9848
-
[7] Loss: 0.01060847844928503
Validation: 0.9819
-
[8] Loss: 0.010371088050305843
Validation: 0.9848
-
[9] Loss: 0.009982218965888023
Validation: 0.9853
-
[10] Loss: 0.00977825652807951
Validation: 0.9838
-
[11] Loss: 0.009571438655257225
Validation: 0.9843
-
[12] Loss: 0.010231235064566135
Validation: 0.9828
-
[13] Loss: 0.011349859647452831
Validation: 0.9838
-
[14] Loss: 0.009434187784790993
Validation: 0.9858
-
[15] Loss: 0.009077513590455055
Validation: 0.9863
-
[16] Loss: 0.008865240961313248
Validation: 0.9848
-
[17] Loss: 0.00882637593895197
Validation: 0.9843
-
[18] Loss: 0.009150735102593899
Validation: 0.9848
-
[19] Loss: 0.008586786687374115
Validation: 0.9838
-
===
end of training
loss afeter training: 0.008388826623558998
params_initializator() is this one:
def params_initializator(size, std=1.0):
return (torch.randn(size)*std).requires_grad_()
validate_epoch is this one:
def batch_accuracy(preds, yb):
corrects = (preds > 0.5) == yb
return corrects.float().mean()
def validate_epoch(model):
accs = [ batch_accuracy( model(xb), yb ) for xb, yb in valid_dl ]
return round( torch.stack(accs).mean().item(), 4 )
Now, I’m not totally sure that everything is working properly. Loss is going down and that’s OK, but there are some differences between my metrics and the book metrics that doesn’t sounds good to me.
Of course, the params are initialized “randomly”, so I can’t have the same metrics than the book, but still, I’m not to sure about them.
In the book example, with 20 epochs, the accuracy shown is this one:
0.8314
0.9017
0.9227
0.9349
0.9438
0.9501
0.9535
0.9564
0.9594
0.9618
0.9613
0.9638
0.9643
0.9652
0.9662
0.9677
0.9687
0.9691
0.9691
0.9696
In the book example, I can see the accuracy slowly going up from 0.831 to 0.969.
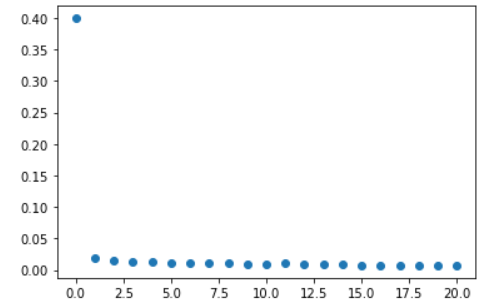
In my case, every single time I try (resetting the params before to train), I get different metrics of course, but I always get the same behaviour: start with a low accuracy (around 0.4) and immediately spike to around 0.98 after only one epoch, then oscillating around this value without improving.
So it sounds too strange to me that the book example got a 97% after 20 epochs and I got a 98.5% after only one epoch.
The same happens with the loss behaviour, it seems to go down extremely fast. I do not have a lot of experience on trained models, but it seems to be quite too fast for me.
Visually, it is even more clear:
LOSS:
ACCURACY
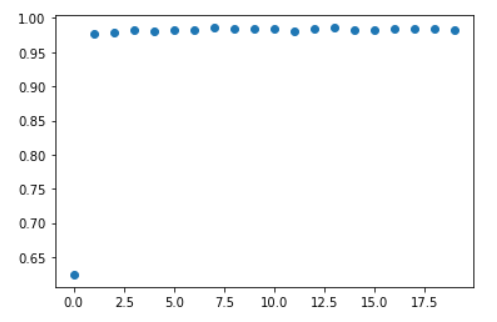
Can somebody with some more experience help me?
Thanks guys ![]()
EDIT:
Just noticed that if I set a lower learning rate, the behaviour is less strange. So maybe, there is nothing wrong here, just me having too much doubt.
Anyway, probably I just try with some digit and see what happens, maybe it’s the smarter way to act in this case.
I’ll do it soon, so it will help to understand further how to use my model, and maybe I’ll discover that it just work properly, and I was just overthinking.
Anyway, I leave the post here, in case someone wants to have a look at it
