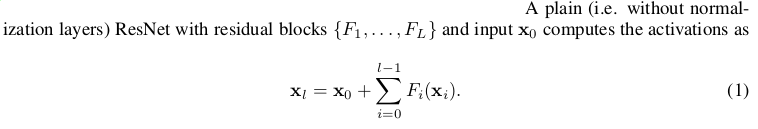Hi, to anyone who wants to go deeper I’d suggest a very nice Paper. “FIXUP INITIALIZATION: RESIDUAL LEARNING WITHOUT NORMALIZATION” introduces a new approach called fixed-update initialization (Fixup). The authors try to solve the exploding and vanishing gradient problem at the beginning of training via properly rescaling a standard initialization. Moreover, they found that training residual networks with Fixup is as stable as training with normalization, and, with proper regularization, it enables residual networks without normalization to achieve state-of-the-art performance in image classification and machine translation. Enjoy the reading!!
Thanks for sharing, Fabrizio.
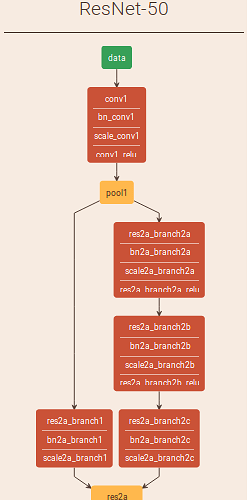
I’m struggling with the definition of residual blocks F and their count L in the paper. Anyone kind enough to draw boxes around F1 and F2 on the ResNet50 below (ignoring the presence of batchnorm layers for a moment)?
Am I told to initialize the weights of the upper conv2d with zeros?
Fixup initialization (or: How to train a deep residual network without normalization)
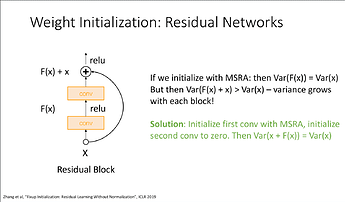
- Initialize the classification layer and the last layer of each residual branch to 0.
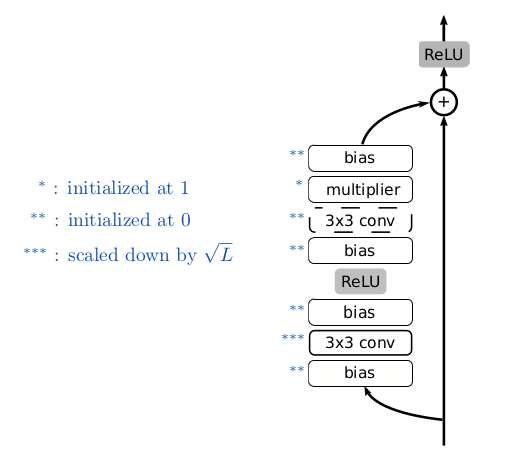
- Initialize every other layer using a standard method (e.g., Kaiming He), and scale only the weight layers inside residual branches by L^(-1/(2*m−2)).
- Add a scalar multiplier (initialized at 1) in every branch and a scalar bias (initialized at 0) before each convolution, linear, and element-wise activation layer.
Hi, look at Resnet block in fastai to have an idea(lesson7), then modify it . L should be the number of those blocks. I didn’t go deep into the paper so I don’t have a clear picture of implementation details.
L seems to be described as the number of residual branches in the network, and the number of blocks is denoted by m. I’m also having a lot of trouble understanding the notation in this paper. As much as I know, in vanilla resnets, there should be only one residual branch (or maybe two, depending on what exactly they mean by it), but if L=1, nothing really makes sense.
I have written a post on Medium, where I have described Fixup from a practitioner’s point of view. Here’s the article
Enjoy!
I cannot quite grasp the \Theta notation here:
\|\Delta f(\mathbf{x})\|=\Theta(\eta) \text { where } \Delta f(\mathbf{x}) \triangleq f\left(\mathbf{x} ; \theta-\eta \frac{\partial}{\partial \theta} \ell(f(\mathbf{x}), \mathbf{y})\right)-f(\mathbf{x} ; \theta)
I understand the second equality but what is the \Theta function in \Theta(\eta)? Does it have to do with the big theta notation?
Here the Θ simply means that we are interested in change that is the same order of magnitude as the learning rate.
Did anyone understand B.1 proof? I didn’t understand the i- and i+ notations
I was watching @jcjohnss new videos on Computer Vision and now I’m confused about Fixup init. If last conv layer in a residual branch is initialized to zero, then there would be no symmetry breaking amongst filters and all the filters learned in that layer would be identical
To clear another doubt, would all elements of a single filter receive the same gradients as well? No, because the local gradient on the weight is going to be equal to to the activations of the previous layer which will be different, so there is symmetry breaking
As long as you don’t have two consecutive layers both initialized at zero, and as long as there is at least one randomly initialized layer on any path from the input to the output, the model will will be able to learn.
But here each filter will receive the same gradients as it goes over the same input/activation. In the last conv layer that was initialized with zeros, all filters learned should be identical. Are redundant features being learnt in the residual layers using Fixup?
Update: I have realized what I was assuming wrong, and for anyone who might have had a similar confusion, I have written about it here https://adityassrana.github.io/blog/theory/2020/08/26/Weight-Init.html