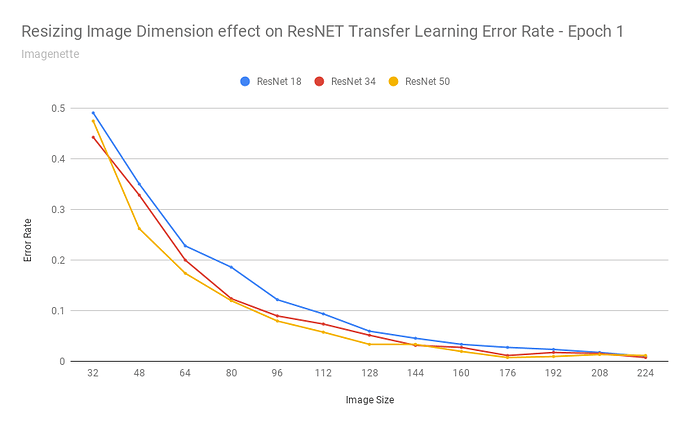
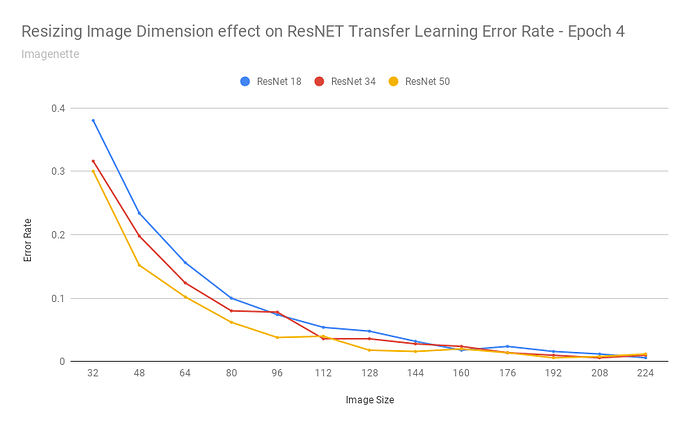
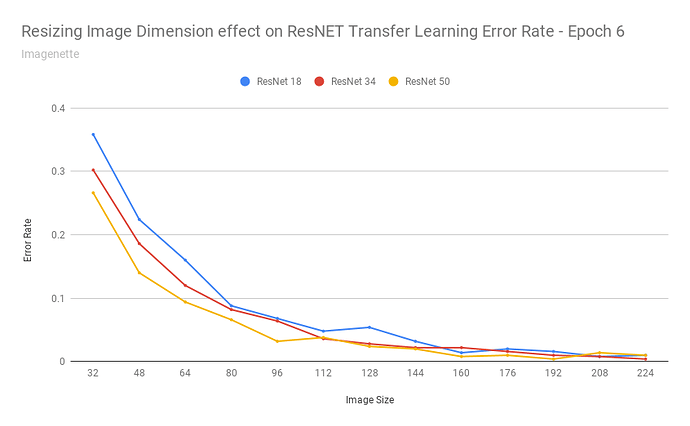
How accurate is transfer learning with resnet34 at different image resolutions? Is this method as effective if the images are scaled down to 192px? 128px? 64px? 32px?
Observations
Visually examining the dataset, I had serious doubts it would be successful as it shrunk to 32px.
Here is the helper to sample the different sizes:
def show(size, rows=2):
data = ImageDataBunch.from_name_re(path_img, fnames, pat, ds_tfms=get_transforms(), size=size, bs=bs
).normalize(imagenet_stats)
data.show_batch(rows)
224:
128:
64:
32:
I would expect a human could could perform the task at 128px, but start to struggle as the images got any smaller. Too much detail was being lost.
Gathering Results
I wrote a helper function: given an image size, calculate the error rates (see the first phase of transfer learning that Jeremy describes in the Lecture 1 Pets training)
def error_rate_of(size:int, cycles:int=4):
data = ImageDataBunch.from_name_re(path_img, fnames, pat, ds_tfms=get_transforms(), size=size, bs=bs
).normalize(imagenet_stats)
learn = cnn_learner(data, models.resnet34, metrics=error_rate)
learn.fit_one_cycle(cycles)
return [float(m[0]) for m in learn.recorder.metrics]
I quickly sampled a few different sizes:
print(error_rate_of(32, 6))
[0.9059540033340454, 0.8660351634025574, 0.8558863401412964, 0.8308525085449219, 0.8281461596488953, 0.8213802576065063]
print(error_rate_of(224, 6))
[0.11705006659030914, 0.08660351485013962, 0.08186738938093185, 0.07780785113573074, 0.07239513099193573, 0.07307171821594238]
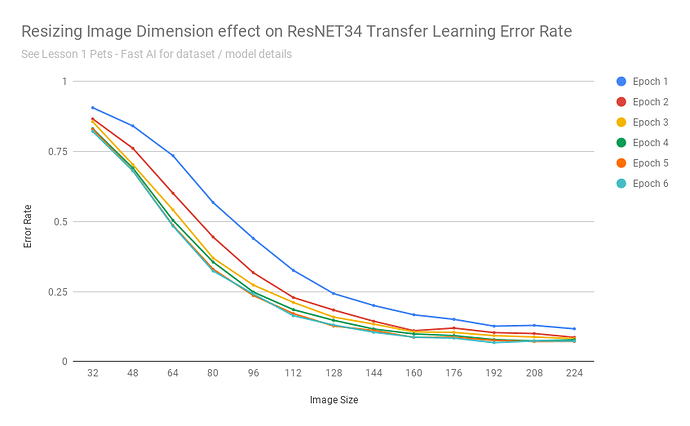
As expected at 32 pixels the model didn’t perform well (achieving 82% error rate after 6 epochs). And a quick test of 224 shows the error rates are correctly being calculated at ~7%.
Next up, let’s running through a range of sizes, saving the error rates for 6 epochs of training:
scores = {}
for size in range(32, 225, 16):
print(size)
scores[size] = error_rate_of(size, 6)
scores
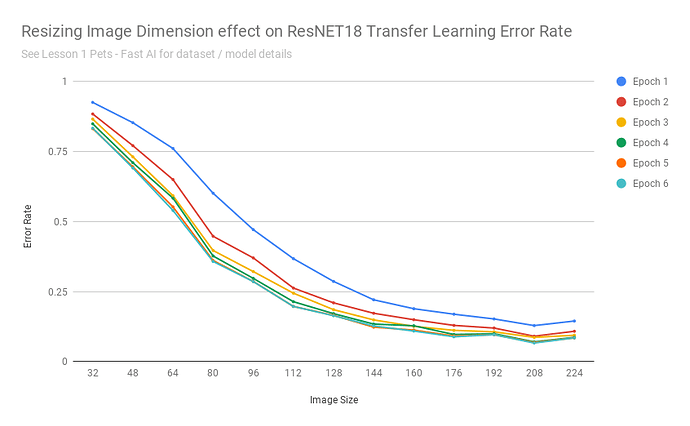
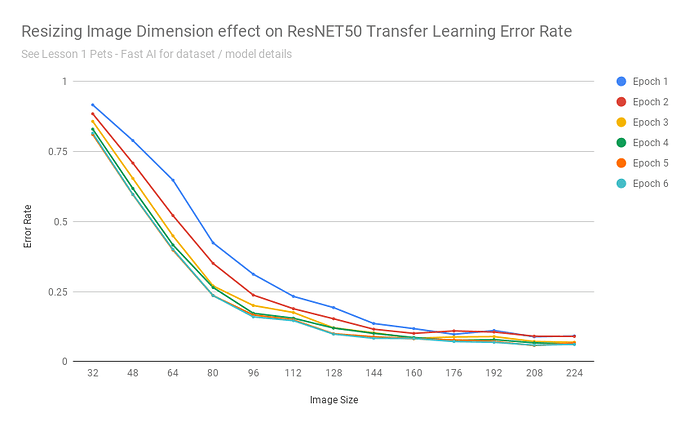
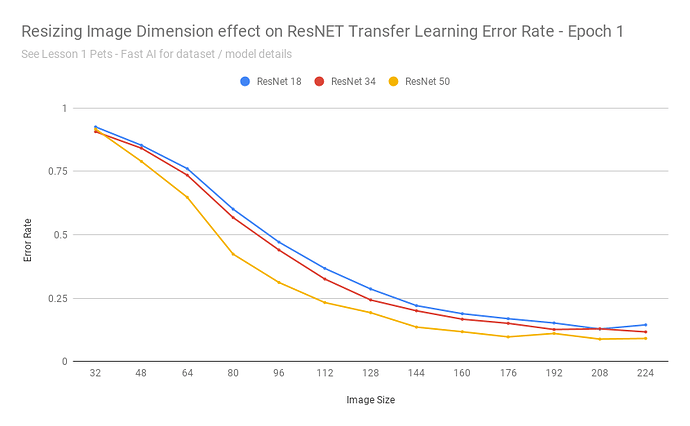
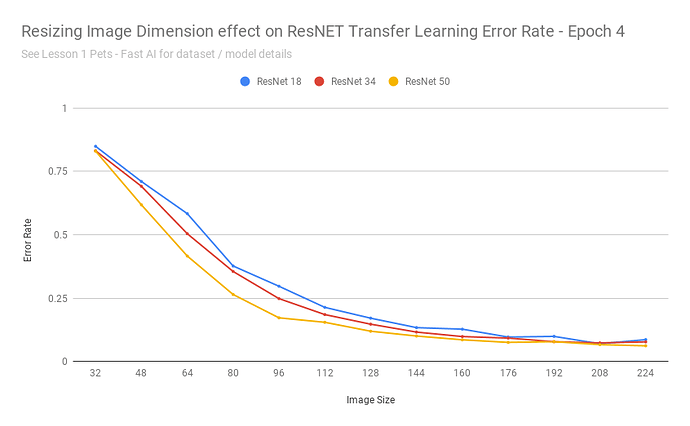
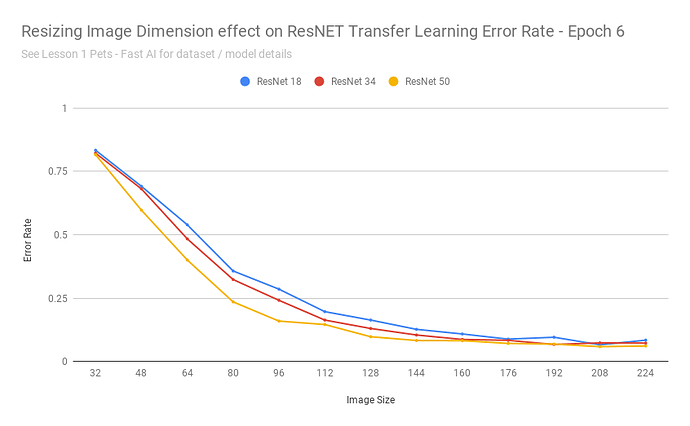
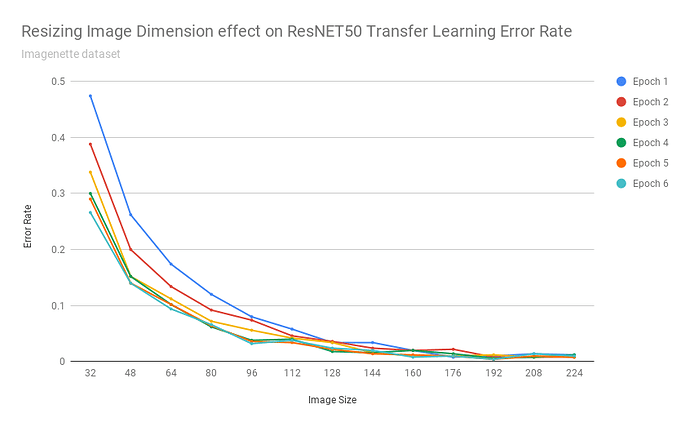
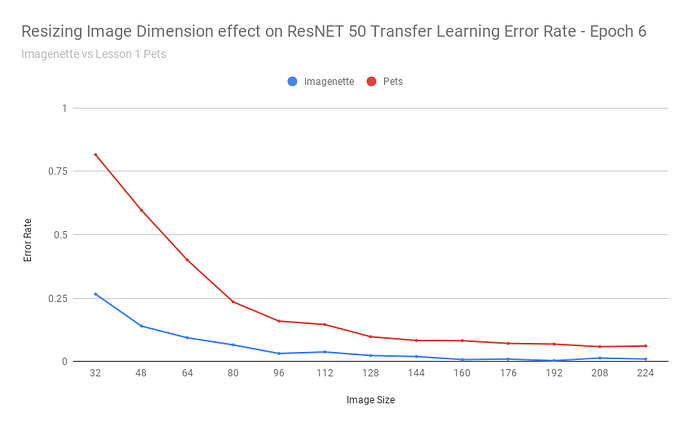
After exporting the scores into a CSV, I was able to build a chart:
Summary
My question was - does it make sense to re-use the weights on different sized images?
That chart seems to say: yes
As the images got really small, it understandable cannot do a good job - as with detecting 37 different breeds of cats/dogs based on 32x32 pixel images is an impossible task even for humans.
Transfer learning performed remarkably consistent for this dataset when images were scaled between 160-224 pixels (and continued to achieve 10% error rates up to ~112 pixels).
In other words: those pretrained resnet34 weights are fairly resolution independent.
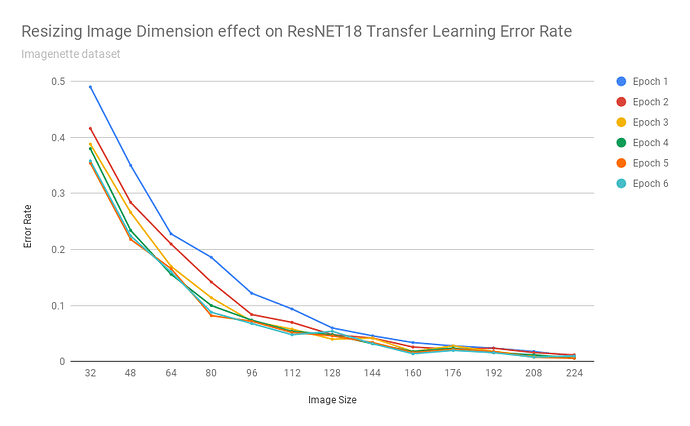
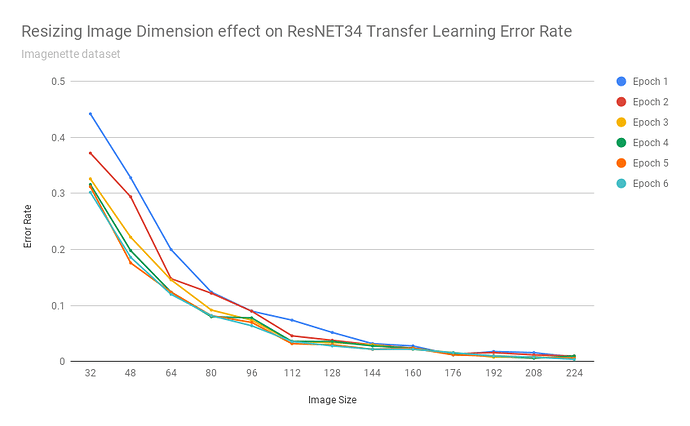
Next steps: with a different dataset that a human can discern at small sizes, test how the accuracy with the transfer learning ResNET scales as images scale down to 32px. (an easy choice might be classifying 37 different classes from imagenet - any ideas for other datasets to try?)