Does the MSE loss of a linear neural network get calculated element wise or sum wise?

Part 2 2022/23
1

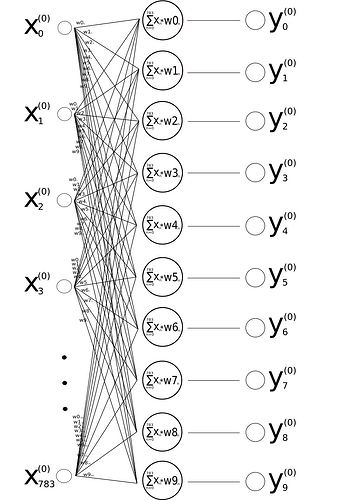
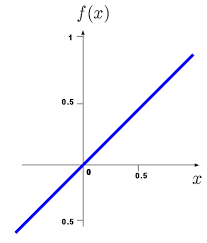
Hey folks,

Assume we’d train a neural network like this …

Testbild6
Testbild6794×1123 147 KB

that gets trained doing a MNIST classification task. Assume the neurons are using linear actiavtions without any hidden layers just like in the above image.

Now my question: If we’d have a linear model like this and the first output vector for y would be

(0, 0, 0, 7, 0, 0, 0, 0, 0, 0 )

If we’d sum that vector up it would be 7. But if the target for training was 7, too but like this

(0, 0, 0, 0, 0, 0, 0, 7, 0, 0)

then the sums would be equal (7=7) and the loss would be zero although the first vector would have placed that value in the wrong position.

So to calculate the loss would we first sum up and then take the difference? Or first take the difference and then sum it up? If we’d take the difference first in this case it would be

(0,0,0,0,7,0,0,0,-7,0,0) Σ = 0

so suming it up afterwards would result in zero loss, too … That seems to be very conflicting … how does a MLP not confuse these calculations randomly?

Can someone explain to me how a linear neural network operates in that sense? From the perspective of loss calculation?

Can a linear neural network have negative values for the activations of its output neurons or its weights, too? In that case I assume it would be highly unlike to have a 7 in a position of a 4, because some negative weights will always drag down the first traget numbers calculation? But I’m not 100% sure about all of the above considerations … Can someone explain this?

2

Hi,

The MSE (Mean Squared Error) loss is calculated element-wise and then averaged across all elements.

  1. Element-wise part:
    The squared errors (differences) are calculated for each corresponding element of the predicted output vector and the target vector. In your example, you have two vectors:
  • Predicted: (0, 0, 0, 7, 0, 0, 0, 0, 0, 0)
  • Target: (0, 0, 0, 0, 0, 0, 0, 7, 0, 0)
    So, for each position i, the loss is (predicted_i - target_i)^2.
  1. Averaging:
    After calculating the squared errors for each element, these values are averaged to get the final loss.
    If we use i index from 0, then the squared errors:
  • For i 0, 1, 2, 4, 5, 6, 8, 9: 0^2 = 0
  • For i 3: 7^2 = 49
  • For i 7: (-7)^2 = 49
    So the total MSE loss 98/10 = 9.8 (we averaging over all 10 elements).
2 Likes
3

Calculating it like that makes a lot of sense! Thank you @AmorfEvo for your structured answer. Are you sure that it is predicted - target? I thought it is target - predicted?

And are all the other losses, for example poisson or abs, also calculated in this style? First: applying mathematical operation on every single (output neuron(activation) - target) second: averaging over total number of output neurons ?

What I also would like to know: can the weights in a linear MLP / linear neural network in the above case be negative, too by the way? I guess so, because neurons with a linear activation function are having the same output value as input sum value like this:

image

1 Like
4

Yes, you are right its target - predicted in the formula, but 2 side notes:

    1. Because of the square it doesn’t matter which is first here - but yes for other losses it can matter.
    1. With pytorch the mse loss 1st parameter is input and the 2nd parameter is target (maybe that’s why I sometimes switch them)
      loss = nn.MSELoss()
      output = loss(input, target)

Yes, other losses work similar way, so mathematical operation and then averaging if its a mean loss.

Yes, any kind of MLP (so linear MLP too) can have negative weights (and usually has) and it can also emit negative outputs.

1 Like
5

When you have questions like these I also suggest to play with code, so you can print out the input, the target, the MLP’s layer(s), everything and just check them :wink:

1 Like
6

Hi,

In my opinion, 'input and ‘target’ are arguments of loss function. Here are params of the MSE:

torch.nn.MSELoss(size_average=None, reduce=None, reduction=‘mean’ )

I fully agree that by default this is element-wise operation and by default second it is reduced to mean :slight_smile:

Have a nice day!