@timlee, I was revising so thought of starting this instead of writing in a personal notebook. Kindly edit and make it awesome as always 
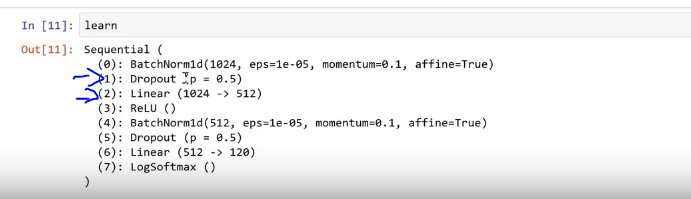
Understanding custom added layers at the end of precomputed model
Lecture video:
These layers can be seen by executing ‘learn’ and these are the only layers we train with precompute True
Linear layer is matrix multiply. Dropout (1024->512) will take 1024 and spit out 512 activations.
ReLU will replace negatives will zero. This is for non-linearity.
Understanding Dropout

Randomly throw half of the activations from a layer.
Understanding p
p=0.5 implies throwing away 50% of activations at random.
p=.01 would imply throwing away 1% of activations at random.
p=.99 would imply throwing away 99% of activations at random.
We could remove dropout by choosing p=0.
Note: 0.5 implies a probability of dropping any cell.
In each mini-batch we throw away random half (with p=0.5). This avoids overfitting. So, if a model has learnt any exact cat/dog/structure then dropping out will help it to generalize well.
So, high p value generalize well while low p will not generalize. Choosing an optimal p is key. Default p is 0.25 for 1st layer, while 0.5 for the second layer. We need more dropout with any bigger model e.g. resnet50.
Since we disable dropout during inference, we see early in training that our validation accuracy is better.
The average number of activations doesn’t change since Pytorch double the remaining activations when we say p=0.5. Maintaining average activations is to ensure we do not change the meaning i.e. losing learnt info.
Question - Which 20% activations are added when we say p=0.2?
Question - Dropout and average without changing the meaning. , After dropout we don’t have that much learning since we add random noise. To me, both questions are related but I’m confused that there are 2 answers. Can anyone clarify
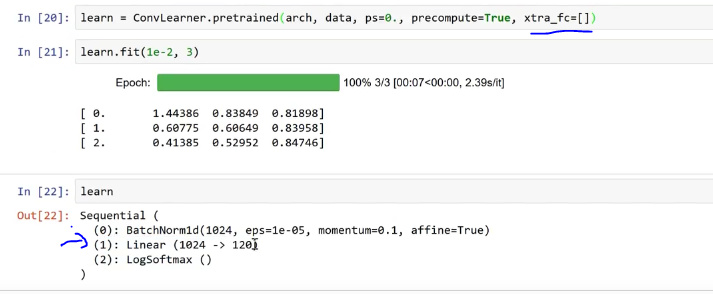
We could choose to say how many additional linear layers our model will have. xtra_fc list will do that work for us. Note: We need to have at least one linear layer which will take the output of our precomputed model and turn that into our classes.
We could specify dropout per layer by passing a list of probabilities:
![]()
To be continued: